မည်သည့် histogram ၏ စံသွေဖည်မှုကို ခန့်မှန်းနည်း

histogram သည် data set တစ်ခုတွင် တန်ဖိုးများ ဖြန့်ဖြူးမှုကို မြင်သာစေရန် အသုံးဝင်သော နည်းလမ်းကို ပံ့ပိုးပေးပါသည်။

ဟစ်စတိုဂရမ်တစ်ခု၏ x-axis သည် ဒေတာတန်ဖိုးအုပ်စုများကို ပြသပြီး y-axis သည် အုပ်စုတစ်ခုစီတွင် ဒေတာအစုတစ်ခုစီတွင် မှတ်သားမှုမည်မျှရှိသည်ကို ပြောပြသည်။

ဟီစတိုဂရမ်တစ်ခုသည် စူးစမ်းလေ့လာမှုများကို bins များအတွင်း ထည့်ထားသောကြောင့်၊ ဟီစတိုဂရမ်ဖြင့် ကိုယ်စားပြုထားသော ဒေတာအစုံ၏ စံသွေဖည်မှုကို အတိအကျ တွက်ချက်ရန် မဖြစ်နိုင်သော်လည်း စံသွေဖည်မှုကို ခန့်မှန်းရန် ဖြစ်နိုင်သည်။

အောက်ပါဥပမာသည် ၎င်းကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသထားသည်။

ဆက်စပ်- မည်သည့် Histogram ၏ ပျမ်းမျှနှင့် အလယ်တန်းကို ခန့်မှန်းနည်း

ဟီစတိုဂရမ်၏ စံသွေဖည်မှုကို ခန့်မှန်းနည်း

ဟီစတိုဂရမ်တစ်ခု၏ စံသွေဖည်မှုကို ခန့်မှန်းရန်၊ ပျမ်းမျှအား ဦးစွာ ခန့်မှန်းရပါမည်။

ပျမ်းမျှအား ခန့်မှန်းရန် အောက်ပါဖော်မြူလာကို အသုံးပြုနိုင်ပါသည်။

ပျမ်းမျှ- Σm _i n _i / N

ရွှေ-

• m _i : i ^th bin ၏ အလယ်
• n _i : i ^th bin ၏ ကြိမ်နှုန်း
• N- စုစုပေါင်းနမူနာအရွယ်အစား

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် အောက်ပါ histogram ရှိသည်ဆိုပါစို့။

ဤအရာသည် ဤ histogram ၏ ပျမ်းမျှတန်ဖိုးကို မည်သို့ ခန့်မှန်းရမည်နည်း။

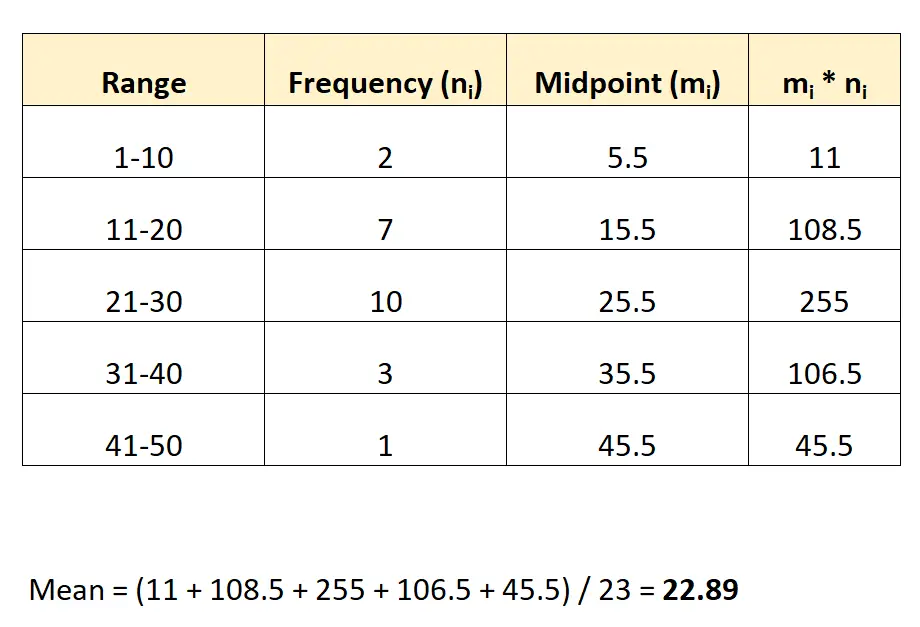
ပျမ်းမျှ 22.89 မှာ ခန့်မှန်းထားပါတယ်။

မှတ်ချက်- အုပ်စုတစ်ခုစီ၏ အလယ်မှတ်ကို အပိုင်းအခြား၏ အောက်နှင့် အထက်တန်ဖိုးများ၏ ပျမ်းမျှအားယူခြင်းဖြင့် တွေ့ရှိနိုင်သည်။ ဥပမာအားဖြင့်၊ ပထမအုပ်စု၏ အလယ်အမှတ်ကို အောက်ပါအတိုင်း တွက်ချက်သည်- (1+10) / 2 = 5.5။

ယခု ကျွန်ုပ်တို့တွင် ပျမ်းမျှခန့်မှန်းချက်တစ်ခုရနေပြီဖြစ်သောကြောင့် စံသွေဖည်မှုကို ခန့်မှန်းရန် အောက်ပါဖော်မြူလာကို အသုံးပြုနိုင်ပါသည်။

စံသွေဖည်: √ Σn _i (m _i -μ) ² / (N-1)

ရွှေ-

• n _i : i ^th bin ၏ ကြိမ်နှုန်း
• m _i : i ^th bin ၏ အလယ်
• µ : ပျမ်းမျှ
• N- စုစုပေါင်းနမူနာအရွယ်အစား

ဤဖော်မြူလာကို ကျွန်ုပ်တို့၏ဒေတာအတွဲတွင် မည်သို့အသုံးပြုရမည်ကို ဤအရာဖြစ်သည်-

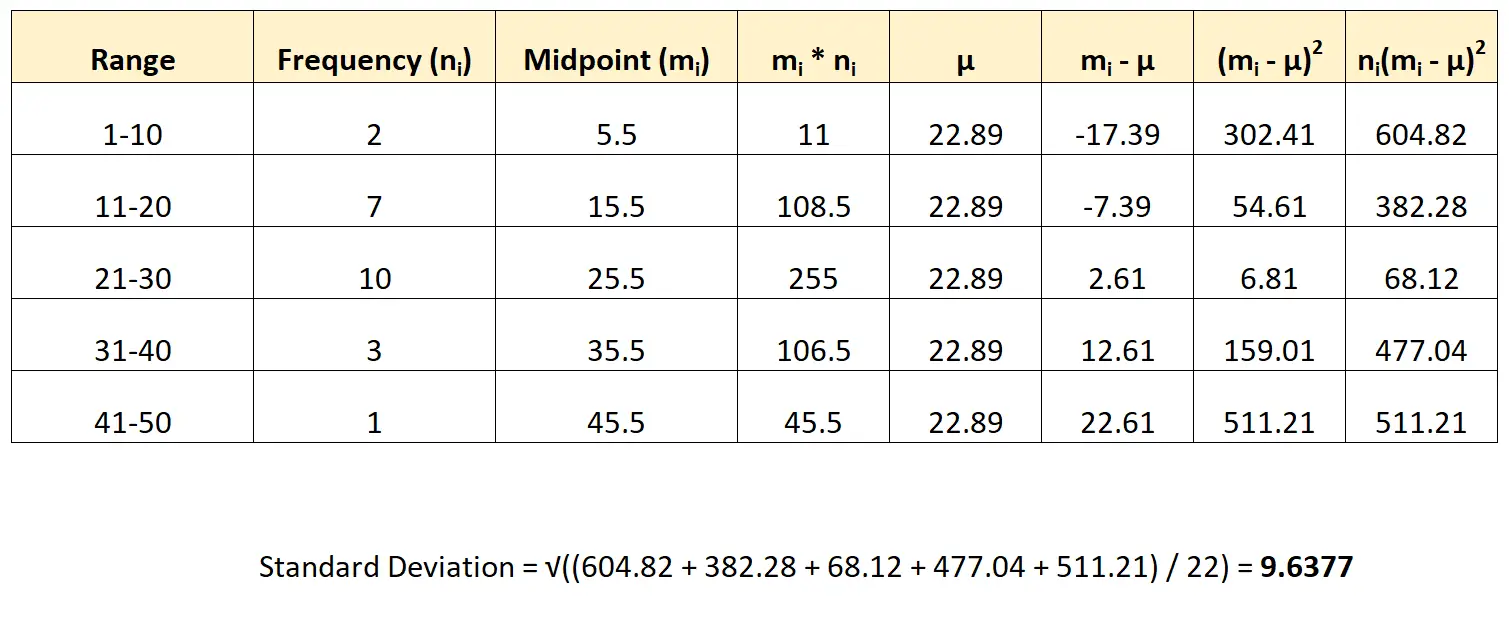ဒေတာအတွဲ၏ စံသွေဖည်မှုကို 9.6377 ဟု ကျွန်ုပ်တို့ ခန့်မှန်းပါသည်။

ဒေတာအတွဲ၏ စံသွေဖည်မှုနှင့် အတိအကျကိုက်ညီရန် အာမမခံနိုင်သော်လည်း (ဒေတာအတွဲ၏ ဒေတာအကြမ်းတန်ဖိုးများကို ကျွန်ုပ်တို့မသိသောကြောင့်) ၎င်းသည် ကျွန်ုပ်တို့၏ အကောင်းဆုံး ခန့်မှန်းချက်ဖြစ်သော စံသွေဖည်မှုကို ကိုယ်စားပြုပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများတွင် အုပ်စုများစုဖွဲ့ထားသော ဒေတာများနှင့် သက်ဆိုင်သည့် အခြားဘုံအလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

အုပ်စုဖွဲ့ဒေတာ၏ကွဲလွဲမှုကို မည်သို့ရှာနိုင်မည်နည်း။
အုပ်စုဖွဲ့ဒေတာ၏ အလယ်အလတ်ကို မည်သို့ရှာရမည်နည်း။
အုပ်စုဖွဲ့ဒေတာမုဒ်ကို ဘယ်လိုရှာမလဲ။