Hypergeometric ဖြန့်ဖြူးမှု

အားဖြင့် Benjamin Anderson ဩဂုတ် 6, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ဟိုက်ပါဂျီဩမေတြီဖြန့်ဝေမှုမှာ အဘယ်နည်းနှင့် ဤဖြန့်ဖြူးမှုအမျိုးအစားဖြင့် ဖြစ်နိုင်ခြေကို တွက်ချက်ပုံကို ရှင်းပြထားပါသည်။ hypergeometric ဖြန့်ဖြူးမှုအတွက် ဖော်မြူလာ၊ ၎င်း၏ဝိသေသလက္ခဏာများအပြင် hypergeometric ဖြန့်ဖြူးမှုဖြစ်နိုင်ခြေကို တွက်ချက်ရန် ဂဏန်းပေါင်းစက်ကို အွန်လိုင်းတွင် သင်တွေ့ရပါမည်။

ဟိုက်ပါဂျီဩမေတြီ ဖြန့်ဖြူးမှုကား အဘယ်နည်း။

ဟိုက်ပါဂျီအိုမက်ထရစ် ဖြန့်ဝေမှုသည် လူဦးရေတစ်ခုမှ n ဒြပ်စင်များကို အစားထိုးခြင်းမရှိဘဲ ကျပန်းထုတ်ယူခြင်းတွင် အောင်မြင်သောကိစ္စရပ်အရေအတွက်ကို ဖော်ပြသည့် ဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။

ဆိုလိုသည်မှာ၊ ၎င်းတို့ထဲမှ တစ်ခုကို အစားထိုးခြင်းမပြုဘဲ လူဦးရေတစ်ခုမှ n ဒြပ်စင်များကို ထုတ်ယူသည့်အခါ x အောင်မြင်မှုများရရှိရန် ဖြစ်နိုင်ခြေကို တွက်ချက်ရန် ဟိုက်ပါဂျီဩမေတြီ ဖြန့်ဖြူးမှုကို အသုံးပြုသည်။

ဟိုက်ပါဂျီအိုမက်ထရစ်ဖြန့်ဝေမှုတွင် ကန့်သတ်ချက်သုံးခုရှိသည်။

N : သည် လူဦးရေရှိ ဒြပ်စင်အရေအတွက် (N = 0၊ 1၊ 2၊…)။
K : သည် အောင်မြင်မှုအများဆုံးအရေအတွက် (K = 0၊ 1၊ 2၊…၊N)။ hypergeometric ဖြန့်ဖြူးမှုတွင် ဒြပ်စင်တစ်ခုကို “ အောင်မြင်မှု” သို့မဟုတ် “ ပျက်ကွက်မှု” ဟုသာယူဆနိုင်သောကြောင့် NK သည် ရှုံးနိမ့်မှုအများဆုံးအရေအတွက်ဖြစ်သည်။
n : ဆိုသည်မှာ အစားထိုးခြင်းမပြုသော ထုတ်ယူမှု အရေအတွက်ဖြစ်သည်။

$X \sim HG(N,K,n)$

ဥပမာအားဖြင့်၊ ဘောင်များ N=8၊ K=5 နှင့် n=3 ပါရှိသော hypergeometric ဖြန့်ဝေမှုပါရှိသော သီးခြားကျပန်းပြောင်းလဲနိုင်သော X ကို အောက်ပါအတိုင်းသတ်မှတ်ထားသည်-

$X \sim HG(8,5,3)$

Hypergeometric ဖြန့်ဝေမှု ဖော်မြူလာ

ဟိုက်ပါဂျီဩမေတြီ ဖြန့်ဖြူးမှုအတွက် ဖော်မြူလာ သည် N နှင့် n ၏ ပေါင်းစပ်နံပါတ် နှင့် ပိုင်းခြားထားသော NK ကျော် NK ၏ ပေါင်းစပ်ကိန်းဂဏန်းဖြင့် x ကျော် K ၏ ပေါင်းစပ်ကိန်းဂဏန်း၏ ရလဒ်ဖြစ်သည်။

N သည် လူဦးရေအရွယ်အစားရှိရာ၊ K သည် နှစ်သက်ဖွယ်ကိစ္စရပ်များ၏ စုစုပေါင်းအရေအတွက်ဖြစ်ပြီး n သည် အစားထိုးခြင်းမပြုဘဲ ထုတ်ယူမှုအရေအတွက်ဖြစ်ပြီး x သည် ဖြစ်ပွားနိုင်ခြေကို တွက်ချက်ရမည်ဖြစ်ပြီး ဖြစ်နိုင်ခြေကို တွက်ချက်ရမည်ဖြစ်သည်။

👉 ဟိုက်ပါဂျီအိုမက်ထရစ် ဖြန့်ဖြူးမှုနောက်ဆက်တွဲဖြစ်သော ကိန်းရှင်တစ်ခု၏ ဖြစ်နိုင်ခြေကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို သင်အသုံးပြုနိုင်သည်။

hypergeometric ဖြန့်ဖြူးမှုဥပမာ

hypergeometric ဖြန့်ဖြူးမှု၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ဖော်မြူလာကို ကျွန်ုပ်တို့တွေ့မြင်ပြီးသည်နှင့်၊ ယခု ကျွန်ုပ်တို့သည် hypergeometric ဖြန့်ဖြူးမှုဖြစ်နိုင်ချေကို တွက်ချက်နည်းကို သင်သိရှိနိုင်စေရန်အတွက် နမူနာတစ်ခုကို အဆင့်ဆင့်ဖြေရှင်းပါမည်။

အိတ်တစ်လုံးတွင် အပြာရောင်ဘောလုံး 20 လုံးနှင့် အနီရောင်ဘောလုံး 30 လုံးထည့်ထားသည်၊ ဆိုလိုသည်မှာ အိတ်အတွင်း၌ စုစုပေါင်းဘောလုံး 50 ရှိသည်။ အကယ်၍ ကျွန်ုပ်တို့သည် မည်သည့်အရာကိုမျှ အစားထိုးခြင်းမရှိဘဲ ဘောလုံး 12 လုံးဆွဲပါက အပြာရောင်ဘောလုံး 4 လုံးဆွဲရန် ဖြစ်နိုင်ခြေကို ရှာပါ။

လေ့ကျင့်ခန်းကိုဖြေရှင်းရန် ပထမဆုံးလုပ်ဆောင်ရမည့်အရာမှာ hypergeometric distribution ၏ parameters များကိုခွဲခြားသတ်မှတ်ရန်ဖြစ်သည်။ ဤကိစ္စတွင်၊ လူဦးရေရှိဒြပ်စင်စုစုပေါင်းအရေအတွက်မှာ 50 ( N =50)၊ အများဆုံးနှစ်သက်ဖွယ်ကိစ္စများတွင် အများဆုံးအရေအတွက်မှာ 20 ( K =20) ဖြစ်ပြီး ဘောလုံး 12 လုံး ( n =12) ဖြစ်သည်။

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

ကျွန်ုပ်တို့သည် အပြာရောင်ဘောလုံး 4 ခု ( x = 4) ကိုဆွဲခြင်း၏ဖြစ်နိုင်ခြေကိုတွက်ချက်လိုသောကြောင့် hypergeometric ဖြန့်ဝေမှုဖော်မြူလာကိုအသုံးပြုကာ ကိန်းရှင်များကို ၎င်းတို့၏သက်ဆိုင်ရာတန်ဖိုးများဖြင့် အစားထိုးပြီး တွက်ချက်မှုလုပ်ဆောင်သည်-

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

Hypergeometric ဖြန့်ဝေဂဏန်းတွက်စက်

လိုချင်သောဖြစ်ရပ်၏ဖြစ်နိုင်ခြေကိုတွက်ချက်ရန် အောက်ဖော်ပြပါအွန်လိုင်းဂဏန်းတွက်စက်ထဲသို့ hypergeometric ဖြန့်ဖြူးမှု၏ဘောင်များကို ထည့်သွင်းပါ။

N သည် လူဦးရေအရွယ်အစားဖြစ်သည်၊ K သည် နှစ်သက်ဖွယ်ကိစ္စရပ်များ၏ စုစုပေါင်းအရေအတွက်ဖြစ်သည်၊ n သည် နမူနာအရွယ်အစားဖြစ်ပြီး x သည် ဤအရာဖြစ်နိုင်ခြေကို ကျွန်ုပ်တို့ရှာဖွေလိုသည့်တန်ဖိုးဖြစ်သည်။

hypergeometric ဖြန့်ဖြူးခြင်း၏လက္ခဏာများ

ဟိုက်ပါဂျီဩမေတြီ ဖြန့်ဖြူးမှုတွင် အောက်ပါ ဂုဏ်သတ္တိများ ရှိသည်။

ဟိုက်ပါဂျီဩမေတြီ ဖြန့်ဖြူးမှု၏ မျှော်မှန်းတန်ဖိုး သည် လူဦးရေရှိ ဒြပ်စင်အရေအတွက်ဖြင့် ပိုင်းခြားထားသော နှစ်သက်ဖွယ်ကိစ္စများ စုစုပေါင်းအရေအတွက်ဖြင့် မြှောက်ထားသော နမူနာရှိ ဒြပ်စင်အရေအတွက်နှင့် ညီမျှသည်။

$E[X]=\cfrac{n\cdot K}{N}$

ဟိုက်ပါဂျီဩမေတြီ ဖြန့်ဖြူးမှုမုဒ်သည် N+2 ဖြင့် ပိုင်းခြားထားသော n+1 အမြှောက် K+1 ၏ ထုတ်ကုန်မှ အဝိုင်းချထားသည့် တန်ဖိုးဖြစ်သည်။

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

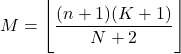
အောက်ဖော်ပြပါ စကားရပ်ကို အသုံးပြု၍ ဟိုက်ပါဂျီဩမေတြီ ဖြန့်ဝေမှု၏ ကွဲလွဲမှုကို ရယူနိုင်သည်။

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

ဟိုက်ပါဂျီဩမေတြီ ဖြန့်ဝေမှု၏ လုပ်ဆောင်ချက်ကို ထုတ်ပေးသည့် အခိုက်အတန့်မှာ အောက်ပါအတိုင်း ဖြစ်သည်။

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

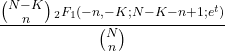
ဟိုက်ပါဂျီဩမေတြီဖြန့်ဝေမှု၏ ဝိသေသလုပ်ဆောင်ချက်မှာ အောက်ပါအတိုင်းဖြစ်သည်။

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

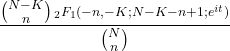
hypergeometric ဖြန့်ဖြူးမှုအတွက် recursive ကို အသုံးပြု၍ ပေးထားသော အရေအတွက် ဖြစ်ရပ်များ ပေါ်ပေါက်နိုင်ခြေကို ယခင်နံပါတ်များ၏ ဖြစ်နိုင်ခြေမှ တွက်ချက်နိုင်သည်-

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

Hypergeometric ဖြန့်ဖြူးခြင်းနှင့် binomial ဖြန့်ဖြူးခြင်း။

ဟိုက်ပါဂျီဩမေတြီ ဖြန့်ဖြူးမှုနှင့် binomial ဖြန့်ဝေမှုကြား ကွာခြားချက်မှာ အစားထိုးခြင်း ဖြစ်သည်။ ပြန်လည်ထုတ်ယူမှုများကို အစားမထိုးသည့်အခါ၊ သို့သော်၊ binomial distribution retrievals များတွင် အစားထိုးသည့်အခါ hypergeometric distribution ကို အသုံးပြုပါသည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် ကတ်ငါးကတ်ကို ကုန်းပတ်တစ်ခုတွင် ကျပန်းဆွဲပြီး အချို့သောကတ်တစ်ခုရနိုင်ခြေကို တွက်ချက်လိုပါက၊ ကျွန်ုပ်တို့ဆွဲသည့်ကတ်တစ်ခုစီကို အစားထိုးခြင်းမရှိပါက၊ တွက်ချက်မှုပြုလုပ်ရန် hypergeometric ဖြန့်ဝေမှုကို အသုံးပြုရမည်ဖြစ်သည်။ သို့သော် နောက်တစ်ကြိမ်ထုတ်ယူခြင်းမပြုမီ ကတ်တစ်ခုကို ဖယ်ရှားသည့်အခါတွင် ၎င်းကို ပြန်ထည့်ပါက၊ ဖြစ်နိုင်ခြေကို တွက်ချက်ရန် binomial distribution ကို အသုံးပြုရပါမည်။

နံပါတ် N သည် ကြီးမားသောအခါ၊ အချိုး N/N သည် သေးငယ်ပြီး နှစ်သက်ဖွယ်ကောင်းသော ကိစ္စများ အရေအတွက်သည် အလွန်သေးငယ်သည်၊၊ ကျွန်ုပ်တို့သည် hypergeometric ဖြန့်ဝေမှုကို binomial ဖြန့်ဝေမှု၏ အနီးစပ်ဆုံးအဖြစ် အသုံးပြုနိုင်ပါသည်။ သို့သော်၊ ရလဒ်သည် ယုံကြည်စိတ်ချရလောက်မည်မဟုတ်သည့်အပြင်၊ hypergeometric ဥပဒေထက် binomial law ဖြင့် ဖြစ်နိုင်ခြေများကို တွက်ချက်ရန် ပိုမိုလွယ်ကူသောကြောင့် ၎င်းကို ကျွန်ုပ်အကြံပြုလိုပါသည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။