အဓိပ္ပါယ်မှာ ခြားနားချက်အတွက် ယူဆချက် စမ်းသပ်ခြင်း။

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ကိန်းဂဏန်းများဆိုင်ရာ သီအိုရီစမ်းသပ်ခြင်း၏ အဓိပ္ပါယ်မှာ မည်ကဲ့သို့ ခြားနားသည်ကို ရှင်းပြထားသည်။ အလားတူ၊ နည်းလမ်းများ၏ ခြားနားချက်နှင့် အဆင့်ဆင့်ဖြေရှင်းထားသော လေ့ကျင့်ခန်းအပေါ် သီအိုရီစမ်းသပ်နည်းကို သင်တွေ့ရှိလိမ့်မည်။

ဆိုလိုရင်းကွာခြားချက်အတွက် ယူဆချက်စမ်းသပ်ခြင်းဆိုသည်မှာ အဘယ်နည်း။

ခြားနားချက်အတွက် တွေးခေါ်မှုဆိုင်ရာ စမ်းသပ်ခြင်း သည် လူဦးရေနှစ်ခု၏ အဓိပ္ပာယ် ကွဲပြားသည်ဟု ယူဆချက်အား ငြင်းပယ်ခြင်း သို့မဟုတ် လက်ခံရန် အသုံးပြုသည့် ကိန်းဂဏန်းဆိုင်ရာ စမ်းသပ်မှုတစ်ခုဖြစ်သည်။ ဆိုလိုသည်မှာ လူဦးရေနှစ်ခု၏ အဓိပ္ပါယ်သည် တူညီခြင်း သို့မဟုတ် ကွဲပြားခြင်းရှိမရှိ ဆုံးဖြတ်ရန် အယူအဆဆိုင်ရာ ခြားနားချက်ကို အသုံးပြုသည်။

သီအိုရီစမ်းသပ်မှုတွင် ပြုလုပ်ခဲ့သော ဆုံးဖြတ်ချက်များသည် ယခင်သတ်မှတ်ထားသော ယုံကြည်မှုအဆင့် ပေါ်တွင် အခြေခံထားကြောင်း မှတ်သားထားပါ၊ ထို့ကြောင့် ယူဆချက်စစ်ဆေးမှုရလဒ်သည် အမြဲတမ်းမှန်ကန်ကြောင်း အာမခံနိုင်သော်လည်း ၎င်းမှာ ဖြစ်နိုင်ခြေအရှိဆုံး ရလဒ်ဖြစ်သည်ကို သတိပြုပါ။

နှစ်ခု၏ခြားနားချက်အတွက် တွေးခေါ်မှုစမ်းသပ်ခြင်းဆိုသည်မှာ စစ်ဆေးမှုစာရင်းအင်းကို တွက်ချက်ခြင်းနှင့် null hypothesis ကို ငြင်းပယ်ခြင်း သို့မဟုတ် မပြုရန် အရေးကြီးသောတန်ဖိုးနှင့် နှိုင်းယှဉ်ခြင်းတို့ ပါဝင်ပါသည်။ အဓိပ္ပါယ်များတွင် ခြားနားချက်အတွက် hypothesis test လုပ်နည်းကို အောက်တွင် တွေ့ရမည်ဖြစ်ပါသည်။

နောက်ဆုံးတွင်၊ စာရင်းဇယားများတွင်၊ သီအိုရီစစ်ဆေးမှုကို တွေးခေါ်မှု ဆန့်ကျင်ဘက်များ၊ သီအိုရီစမ်းသပ်ခြင်း သို့မဟုတ် အရေးပါမှုစမ်းသပ်ခြင်းဟုလည်း ခေါ်ဆိုနိုင်သည်ကို သတိရပါ။

➤ အဓိပ္ပါယ်မှာ ကွဲပြားမှု၏နမူနာခွဲဝေမှုကို ကြည့်ပါ။

အဓိပ္ပါယ်များတွင် ကွဲပြားမှုအတွက် အယူအဆဆိုင်ရာ စမ်းသပ်မှုဖော်မြူလာ

ခြားနားချက်ဆိုင်ရာ ယူဆချက်များအား စမ်းသပ်ရန် အသုံးပြုသင့်သော ဖော်မြူလာကို ဆိုလိုသည်မှာ လူဦးရေကွဲလွဲမှုကို သိရှိခြင်းရှိမရှိနှင့် မတူပါက ၎င်းတို့ကို တူညီသည် သို့မဟုတ် ကွဲပြားသည်ဟု ယူဆနိုင်သည်ဆိုသည်အပေါ် မူတည်၍ ကွဲပြားသည်။ ဒါကြောင့် ဒီကဏ္ဍမှာ ဘယ်ပုံသေနည်းကို အသုံးပြုရမလဲဆိုတာကို ကြည့်ရပါမယ်။

လူသိများသော ကွဲပြားမှုများ

ကွဲလွဲမှုများကို သိရှိသောအခါ ခြားနားချက်အတွက် ပေါင်းစပ်ယူဆချက် စမ်းသပ်ကိန်းဂဏန်းကို တွက်ချက်ခြင်းအတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်-

$\displaystyle Z=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

ရွှေ-

$Z$

စံပုံမှန်ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သော သိထားသောကွဲလွဲမှုဖြင့် ဆိုလိုချက်နှစ်ခု၏ ခြားနားချက်အတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းဖြစ်ပါသည်။
$\mu_1$

လူဦးရေရဲ့ ပျမ်းမျှ ကိန်းဂဏန်းက ၁။
$\mu_2$

လူဦးရေ ပျမ်းမျှ ၂။
$\overline{x_1}$

နမူနာ 1 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
$\overline{x_2}$

နမူနာ 2 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
$\sigma_1$

လူဦးရေ ၁ ၏ စံသွေဖည်သည်။
$\sigma_2$

လူဦးရေ ၂ ၏ စံသွေဖည်သည်။
$n_1$

နမူနာအရွယ်အစား 1 ဖြစ်ပါတယ်။
$n_2$

နမူနာအရွယ်အစား 2 ဖြစ်ပါတယ်။

ဤသည်မှာ အဖြစ်အများဆုံးကိစ္စဖြစ်သည်၊ ထို့ကြောင့် ဤဖော်မြူလာကို အချို့သောကိစ္စများတွင်သာ အသုံးပြုပါသည်။

အမည်မသိနှင့် တန်းတူသွေဖီသည်။

လူဦးရေကွဲလွဲမှုကို မသိရသော်လည်း ညီမျှသည်ဟု ယူဆသည့်အခါ ခြားနားချက်အတွက် ပေါင်းစပ်ယူဆချက် စမ်းသပ်ကိန်းဂဏန်းကို တွက်ချက်ရန် ဖော်မြူလာမှာ –

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

ရွှေ-

$t$

ကျောင်းသားတစ်ဦး၏ t ဖြန့်ဝေမှုနောက်တွင် လွတ်မြောက်မှု n ₁ + n ₂ -2 ဒီဂရီဖြင့် ကျောင်းသားတစ်ဦး၏ t ဖြန့်ဝေမှုနောက်တွင် အမည်မသိကွဲလွဲမှုများရှိသည့် အဓိပ္ပါယ်များတွင် ခြားနားချက်အတွက် သီအိုရီစမ်းသပ်ကိန်းဂဏန်းဖြစ်သည်။
$\mu_1$

လူဦးရေရဲ့ ပျမ်းမျှ ကိန်းဂဏန်းက ၁။
$\mu_2$

လူဦးရေ ပျမ်းမျှ ၂။
$\overline{x_1}$

နမူနာ 1 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
$\overline{x_2}$

နမူနာ 2 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
$s_p$

စံသွေဖည်ပေါင်းစပ်မှုဖြစ်သည်။
$n_1$

နမူနာအရွယ်အစား 1 ဖြစ်ပါတယ်။
$n_2$

နမူနာအရွယ်အစား 2 ဖြစ်ပါတယ်။

နမူနာနှစ်ခု၏ ပေါင်းစပ်စံသွေဖည်မှုကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

အမည်မသိနှင့် မတူညီသော ကွဲပြားမှုများ

လူဦးရေကွဲလွဲမှုကို မသိနိုင်သည့်အပြင်၊ ၎င်းတို့သည် ကွဲပြားသည်ဟု ယူဆသောအခါ၊ အဓိပ္ပါယ်များတွင် ခြားနားချက်အတွက် သီအိုရီစမ်းသပ်ကိန်းဂဏန်းတွက်ချက်ခြင်းဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်-

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

ရွှေ-

$t$

ကျောင်းသား၏ t ဖြန့်ဝေမှုကို လိုက်နာသော အမည်မသိကွဲလွဲမှုများဖြင့် ခြားနားချက်အတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းများဖြစ်သည်။
$\mu_1$

လူဦးရေရဲ့ ပျမ်းမျှ ကိန်းဂဏန်းက ၁။
$\mu_2$

လူဦးရေ ပျမ်းမျှ ၂။
$\overline{x_1}$

နမူနာ 1 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
$\overline{x_2}$

နမူနာ 2 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
$\sigma_1$

လူဦးရေ ၁ ၏ စံသွေဖည်သည်။
$\sigma_2$

လူဦးရေ ၂ ၏ စံသွေဖည်သည်။
$n_1$

နမူနာအရွယ်အစား 1 ဖြစ်ပါတယ်။
$n_2$

နမူနာအရွယ်အစား 2 ဖြစ်ပါတယ်။

သို့ရာတွင်၊ ဤကိစ္စတွင်၊ ကျောင်းသား၏ t ဖြန့်ဖြူးမှု၏ လွတ်လပ်မှုဒီဂရီကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ နည်းလမ်းများ၏ ခြားနားချက်အတွက် ယုံကြည်မှု ကြားကာလ ဖော်မြူလာကို ကြည့်ပါ။

ခြားနားချက်အတွက် ခိုင်မာသော သဘောတရားကို စမ်းသပ်ခြင်း၏ ဥပမာကို ဆိုလိုသည်။

နည်းလမ်းများ၏ ခြားနားချက်အပေါ် သီအိုရီစမ်းသပ်ခြင်း၏ သဘောတရားကို ပေါင်းစည်းခြင်းအား အပြီးသတ်ရန်၊ ဤယူဆချက်စမ်းသပ်ခြင်းအမျိုးအစား၏ ခိုင်မာသော ဥပမာတစ်ခုကို ကျွန်ုပ်တို့တွေ့ရပါမည်။

အထူးသဖြင့် ကုမ္ပဏီနှစ်ခု၏ ပျမ်းမျှလစာကွာခြားမှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် ပြိုင်ဘက်ကုမ္ပဏီနှစ်ခု၏ လစာနှင့်ပတ်သက်သည့် ကိန်းဂဏန်းလေ့လာမှုတစ်ခု ပြုလုပ်လိုပါသည်။ ထိုသို့လုပ်ဆောင်ရန်အတွက် ကုမ္ပဏီတစ်ခုမှ အလုပ်သမား ၄၇ ဦးနှင့် အခြားကုမ္ပဏီမှ အလုပ်သမား ၅၅ ဦး၏ နမူနာကို ယူဆောင်သွားမည်ဖြစ်သည်။ ပျမ်းမျှလစာ $40,000 နှင့် standard deviation $12,000 ကို ပထမနမူနာမှ ရရှိပြီး ပျမ်းမျှလစာ $46,000 နှင့် standard deviation $18,000 ကို ဒုတိယနမူနာမှ ရရှိပါသည်။ ပျမ်းမျှလစာ ကွာခြားမှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် 5% အရေးပါမှု အဆင့်ဖြင့် သီအိုရီ စမ်းသပ်မှု ပြုလုပ်ပါ။

ဤကိစ္စတွင်၊ အဓိပ္ပါယ်နှစ်မျိုး၏ ခြားနားချက်အတွက် null hypothesis နှင့် အခြား hypothesis တို့သည် အောက်ပါအတိုင်းဖြစ်သည် ။

$\begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}$

ဤအခြေအနေတွင်၊ လူဦးရေကွာဟမှုကို မသိရသော်လည်း ၎င်းတို့သည် ပြိုင်ဆိုင်နေသော ကုမ္ပဏီများနှင့် ၎င်းတို့လုပ်ကိုင်နေသော ဈေးကွက်၏ လုပ်ငန်းခွင်အခြေအနေများသည် တူညီသောကြောင့် တူညီသည်ဟု ယူဆနိုင်သည်။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့အသုံးပြုသင့်သော ခြားနားချက်အတွက် သီအိုရီစမ်းသပ်ကိန်းဂဏန်းအတွက် ဖော်မြူလာမှာ-

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

ထို့ကြောင့် နမူနာနှစ်ခု၏ စုပေါင်းစံသွေဖည်မှုကို တွက်ချက်သည်-

$\begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}$

ယခု ကျွန်ုပ်တို့သည် ဆိုလိုသည်မှာ ခြားနားချက်အတွက် တွေးခေါ်မှုစမ်းသပ်ခြင်းဖော်မြူလာကို ကျင့်သုံးသည်-

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}=\cfrac{(40000-46000)-0}{\displaystyle 15530,61\sqrt{\frac{1}{47}+\frac{1}{55}}}=-1,94$

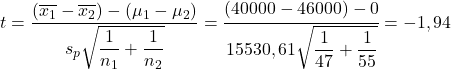
အခြားတစ်ဖက်တွင်၊ Student’s t table ရှိ အဓိပ္ပါယ်များ ခြားနားချက်အတွက် hypothesis test ၏ အရေးပါသောတန်ဖိုးကို ကျွန်ုပ်တို့ ရှာဖွေနေပါသည်။

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}$

ထို့နောက်၊ စစ်ဆေးမှုစာရင်းအင်း၏ ပကတိတန်ဖိုးသည် အရေးကြီးသောစမ်းသပ်မှုတန်ဖိုးထက် နည်းသောကြောင့်၊ null hypothesis ကို လက်ခံပြီး အခြား hypothesis ကို ပယ်ချပါသည်။

$|-1,94|=1,94<1,984 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

ဆိုလိုရင်းကွာခြားချက်အတွက် ယူဆချက်စမ်းသပ်ခြင်းဆိုသည်မှာ အဘယ်နည်း။

အဓိပ္ပါယ်များတွင် ကွဲပြားမှုအတွက် အယူအဆဆိုင်ရာ စမ်းသပ်မှုဖော်မြူလာ

လူသိများသော ကွဲပြားမှုများ

အမည်မသိနှင့် တန်းတူသွေဖီသည်။

အမည်မသိနှင့် မတူညီသော ကွဲပြားမှုများ

ခြားနားချက်အတွက် ခိုင်မာသော သဘောတရားကို စမ်းသပ်ခြင်း၏ ဥပမာကို ဆိုလိုသည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မှတ်ချက်တစ်ခုထည့်ပါ။