Interpolation သို့မဟုတ် extrapolation- ကွာခြားချက်ကား အဘယ်နည်း။

စာရင်းဇယားများတွင် ကျောင်းသားများ မကြာခဏ ရောထွေးနေသော ဝေါဟာရနှစ်ခုမှာ ပေါင်းစည်းခြင်း နှင့် အပိုဆောင်းခြင်း ဖြစ်သည်။

ဤတွင် ကွာခြားချက်မှာ-

Interpolation ဆိုသည်မှာ ဒေတာအချက်အကွာအဝေး အတွင်း ကျရောက်သော တန်ဖိုးများကို ခန့်မှန်းခြင်းအား ရည်ညွှန်းသည်။

Extrapolation ဆိုသည်မှာ ဒေတာအချက်အကွာအဝေး၏ ပြင်ပတွင် ကျရောက်နေသော တန်ဖိုးများကို ခန့်မှန်းခြင်းအား ရည်ညွှန်းသည်။

အောက်ပါဥပမာသည် ဝေါဟာရနှစ်ခုကြား ခြားနားချက်ကို ဖော်ပြသည်။

ဥပမာ- interpolation နှင့် extrapolation

ကျွန်ုပ်တို့တွင် အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။

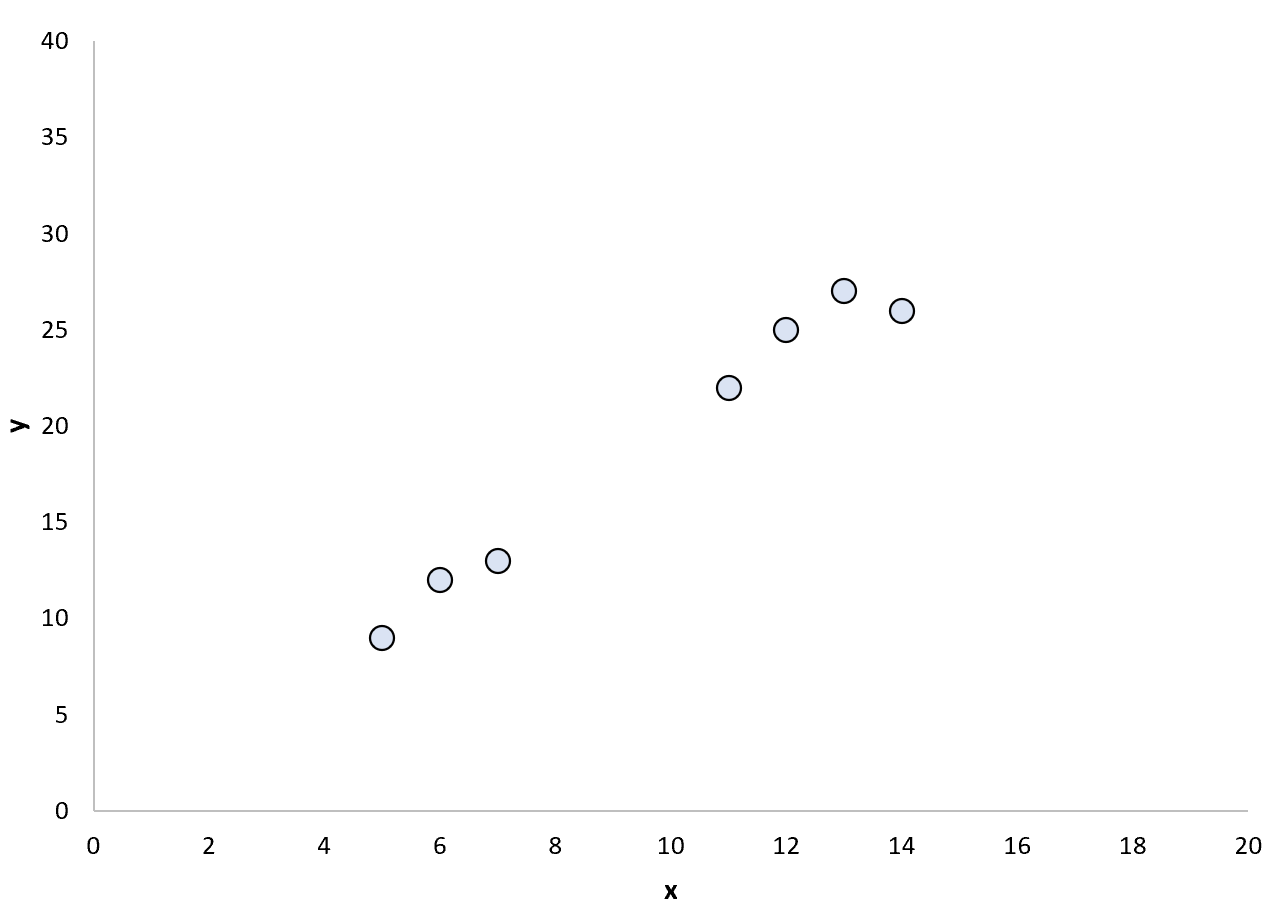
ရိုးရှင်းသော linear regression model ကို ဤအချက်များနှင့် ကိုက်ညီရန် ဆုံးဖြတ်နိုင်သည်-

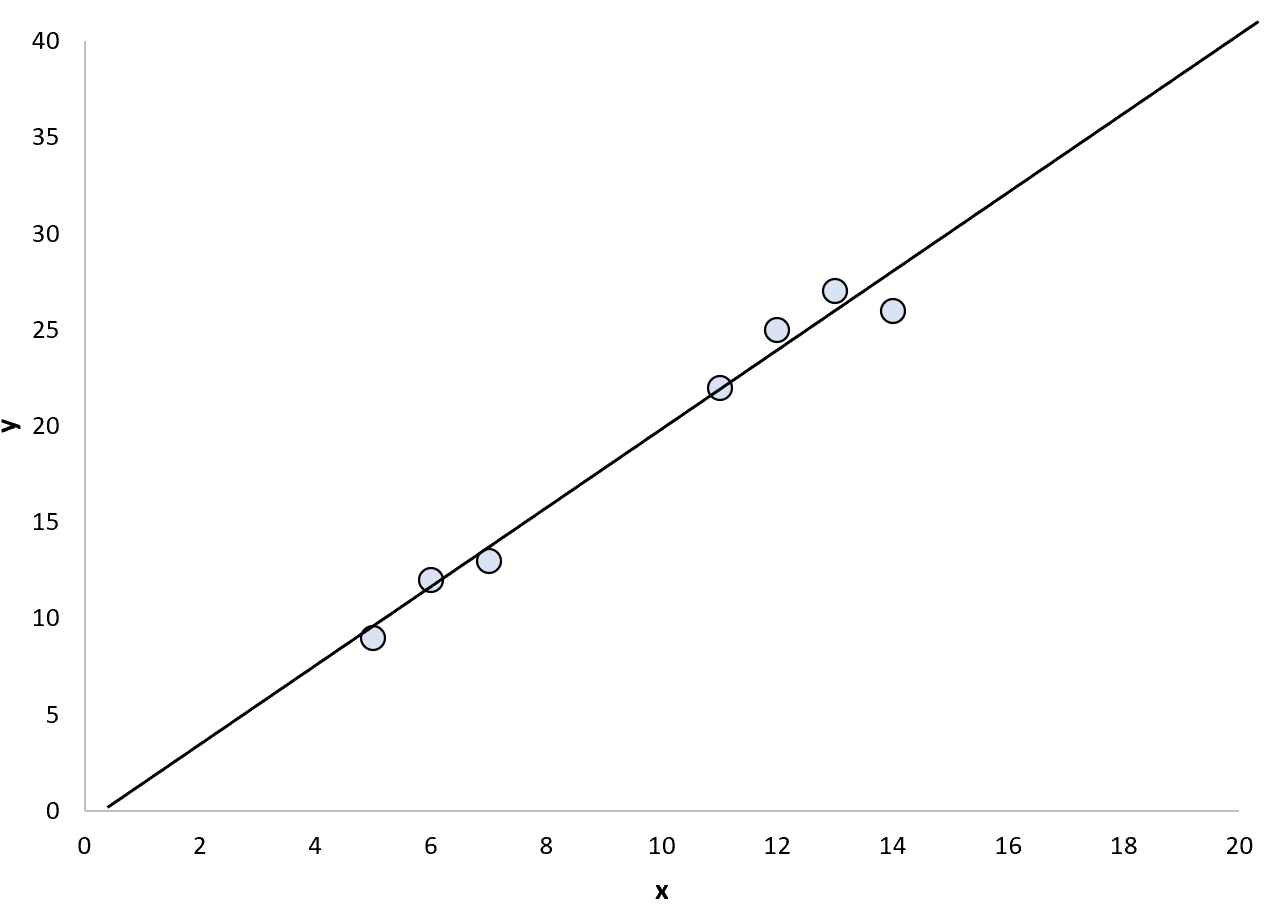
ထို့နောက် ကျွန်ုပ်တို့သည် ဒေတာအမှတ်အကွာအဝေး အတွင်း နှင့် အပြင်ဘက်ရှိ အမှတ်တန်ဖိုးများကို ခန့်မှန်းရန် တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုပုံစံကို အသုံးပြုနိုင်သည်။

လက်ရှိဒေတာအမှတ်အကွာအဝေးအတွင်း အမှတ်တန်ဖိုးများကို ခန့်မှန်းရန် တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုပုံစံကို ကျွန်ုပ်တို့အသုံးပြုသောအခါ ၎င်းကို interpolation ဟုခေါ်သည်။

အပြန်အလှန်အားဖြင့်၊ ကျွန်ုပ်တို့သည် ရှိပြီးသားအကွာအဝေးအပြင်ဘက်ရှိ အမှတ်တန်ဖိုးများကို ခန့်မှန်းရန် တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုပုံစံကို အသုံးပြုသောအခါ၊ ၎င်းကို အပိုဆောင်းခြင်း ဟုခေါ်သည်။

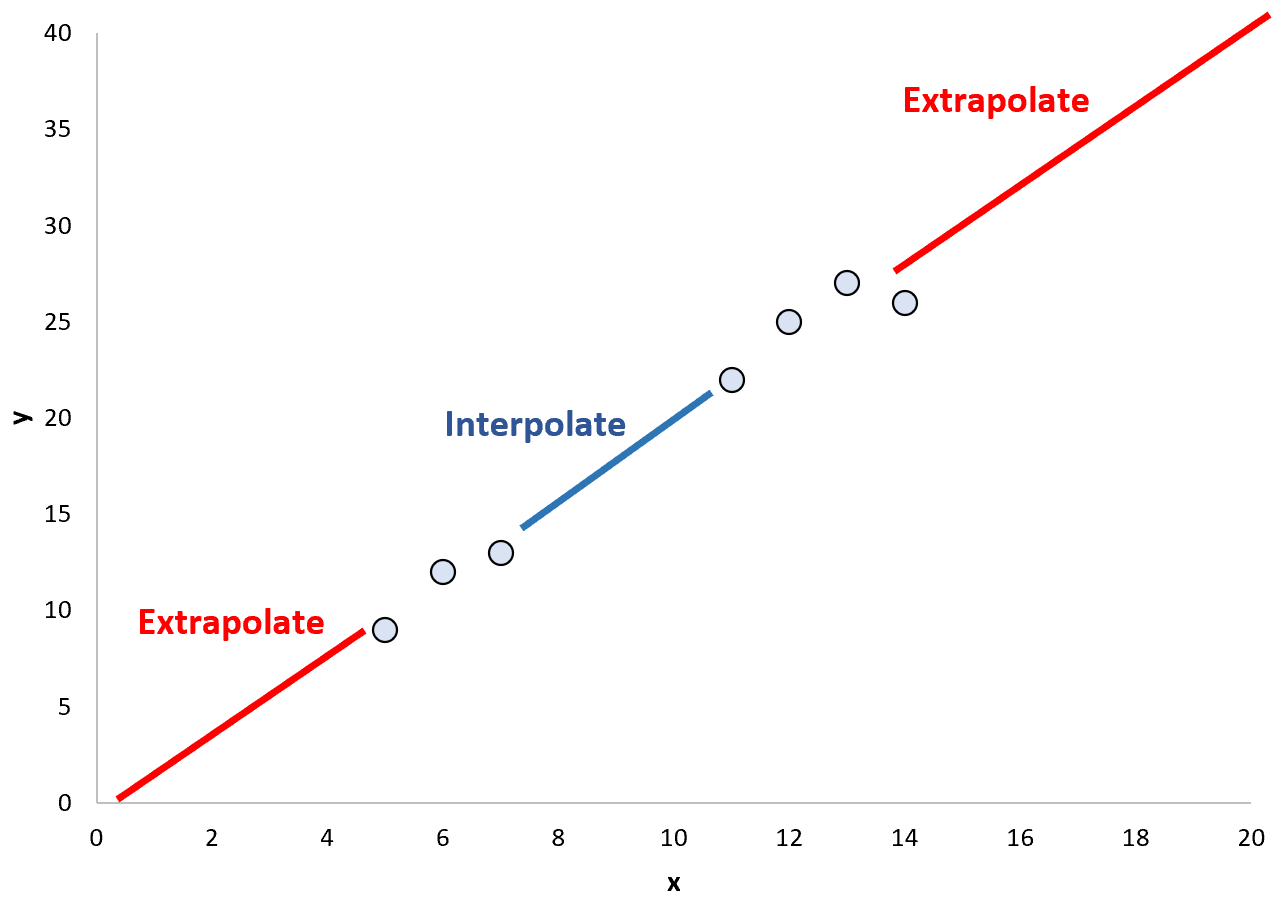
ထုတ်ယူခြင်း၏အလားအလာ

ကျွန်ုပ်တို့ အပိုဆောင်းသည့်အခါ၊ လက်ရှိဒေတာအကွာအဝေးအတွင်းရှိ တူညီသောပုံစံသည်လည်း အပိုင်းအခြားပြင်ပတွင် ရှိနေသည်ဟု ကျွန်ုပ်တို့ယူဆပါသည်။

သို့ရာတွင်၊ ၎င်းသည် အန္တရာယ်ရှိသော ယူဆချက်တစ်ခု ဖြစ်နိုင်သောကြောင့်၊ လက်ရှိဒေတာအကွာအဝေး၏ အပြင်ဘက်တွင်ရှိသော ပုံစံသည် အလွန်ကွာခြားသောကြောင့် ဖြစ်နိုင်သည်-

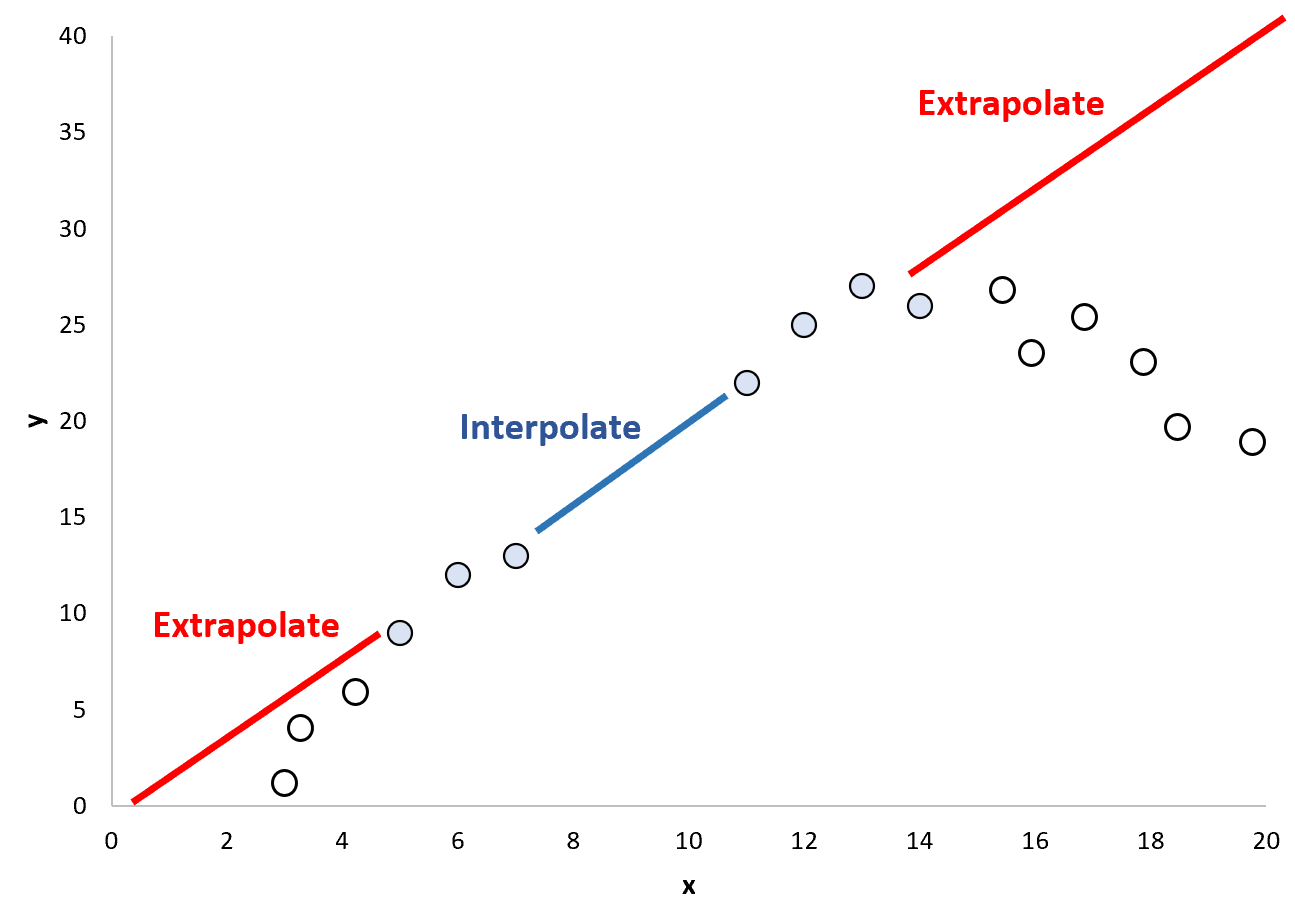
ဤအကြောင်းကြောင့်၊ ဆုတ်ယုတ်မှုပုံစံကိုဖန်တီးရန် အသုံးပြုသည့် တန်ဖိုးများ၏အကွာအဝေးအပြင်ဘက်တွင် ကျရောက်နေသော ဒေတာအမှတ်တန်ဖိုးများကို ခန့်မှန်းရန် အပိုဆောင်းအသုံးပြုခြင်းသည် အန္တရာယ်ရှိနိုင်သည်။

လက်တွေ့တွင်၊ ရှိရင်းစွဲတန်ဖိုးများအကွာအဝေးထက် အနည်းငယ်ကျနေသည့် အမှတ်တန်ဖိုးများကို ခန့်မှန်းရန် အပိုပိုရေးရှင်းကို အသုံးပြုခြင်းသည် မကြာခဏ အဓိပ္ပာယ်ရှိသော်လည်း အပိုင်းအခြားတစ်ခုမှ ကျော်လွန်သွားလေလေ၊ ခန့်မှန်းတန်ဖိုးနှင့် အမှန်တကယ် ကွာဟချက် ပိုများလေဖြစ်သည်။ တန်ဖိုးက အရေးကြီးတယ်။ .

extrapolation ကို ဘယ်အချိန်မှာ သုံးမလဲ။

အပိုဆောင်းခြင်းသည် ကျိုးကြောင်းဆီလျော်သော အကြံဥာဏ်ဟုတ်၊

ဥပမာအားဖြင့်၊ ကုမ္ပဏီတစ်ခု၏ စျေးကွက်ရှာဖွေရေးဌာနတစ်ခုသည် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် ကြော်ငြာအသုံးစရိတ်ကို ခန့်မှန်းသူကိန်းရှင်နှင့် စုစုပေါင်းဝင်ငွေအဖြစ် ကြော်ငြာအသုံးစရိတ်ကို အသုံးပြုကာ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံကို အသုံးပြုသည်ဆိုပါစို့။

ဤအခြေအနေတွင်၊ ကြော်ငြာအသုံးစရိတ်များ ဆက်တိုက်တိုးလာခြင်းသည် စုစုပေါင်းဝင်ငွေအတွက် ကြိုတင်မှန်းဆနိုင်သော တိုးလာမည်ဟု ယူဆနိုင်သည်-

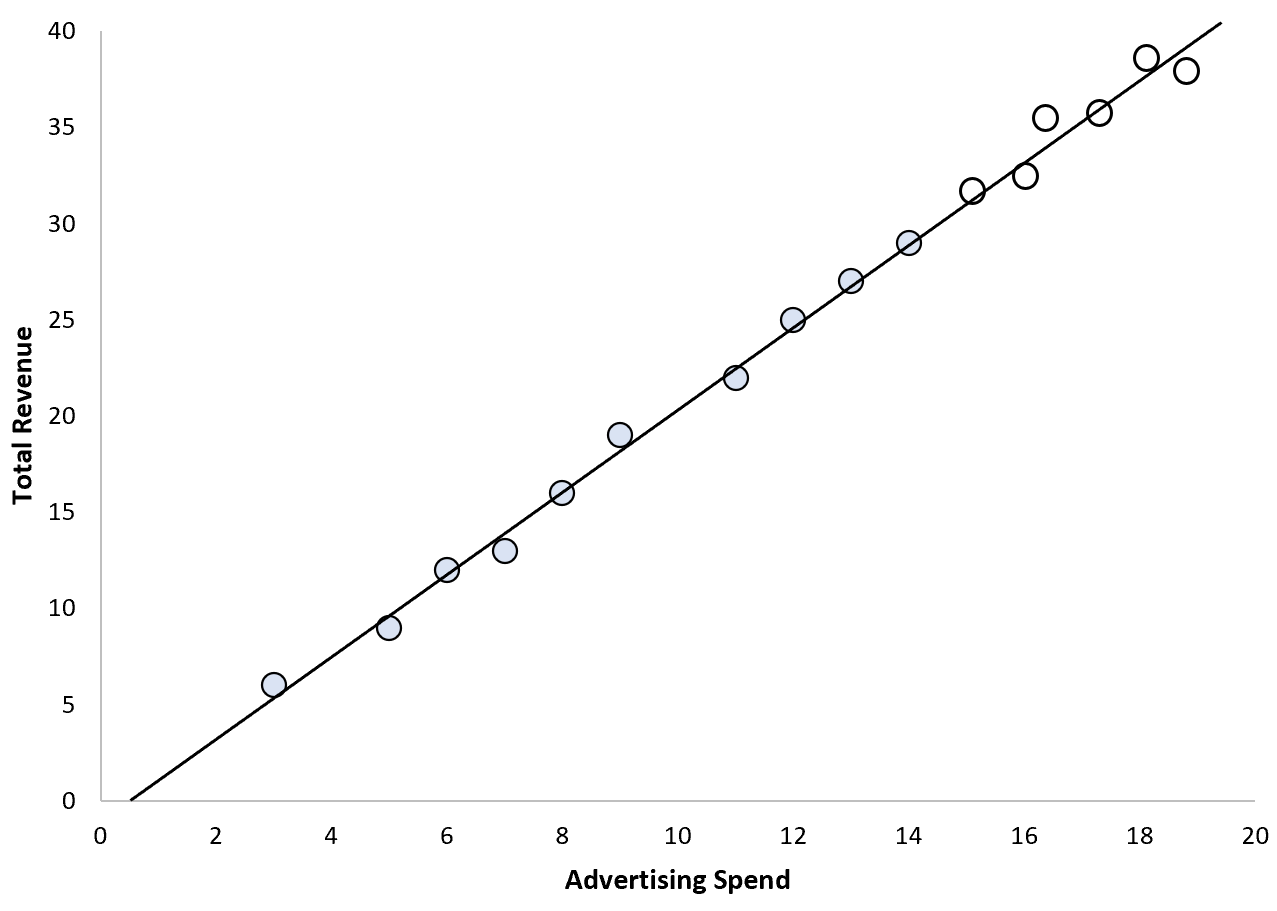
ဤအခြေအနေမျိုးတွင်၊ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏တန်ဖိုးများကို ခွဲထုတ်နိုင်စွမ်းအပေါ် အလွန်ယုံကြည်စိတ်ချနိုင်ပါသည်။

သို့ရာတွင်၊ ဇီဝဗေဒပညာရှင်တစ်ဦးသည် အပင်ကြီးထွားမှုကို ခန့်မှန်းရန် စုစုပေါင်းဓာတ်မြေသြဇာကို အသုံးပြုလိုသည့် အဖြစ်အပျက်တစ်ခုကို သုံးသပ်ကြည့်ပါ။

သူမသည် ရိုးရှင်းသော linear regression model ကို data point နှင့် အံဝင်ခွင်ကျဖြစ်အောင် ဆုံးဖြတ်နိုင်သည်၊ သို့သော် အပင်အမြင့်အတွက် ကန့်သတ်ချက်ရှိသောကြောင့် အမှတ်တန်ဖိုးများကို ခန့်မှန်းရန် extrapolation ကိုအသုံးပြုခြင်းသည် အဓိပ္ပာယ်မရှိပေ။ တန်ဖိုးဘောင်အပြင်ဘက်။ မော်ဒယ်နှင့်ကိုက်ညီရန်အသုံးပြုသောတန်ဖိုးများ

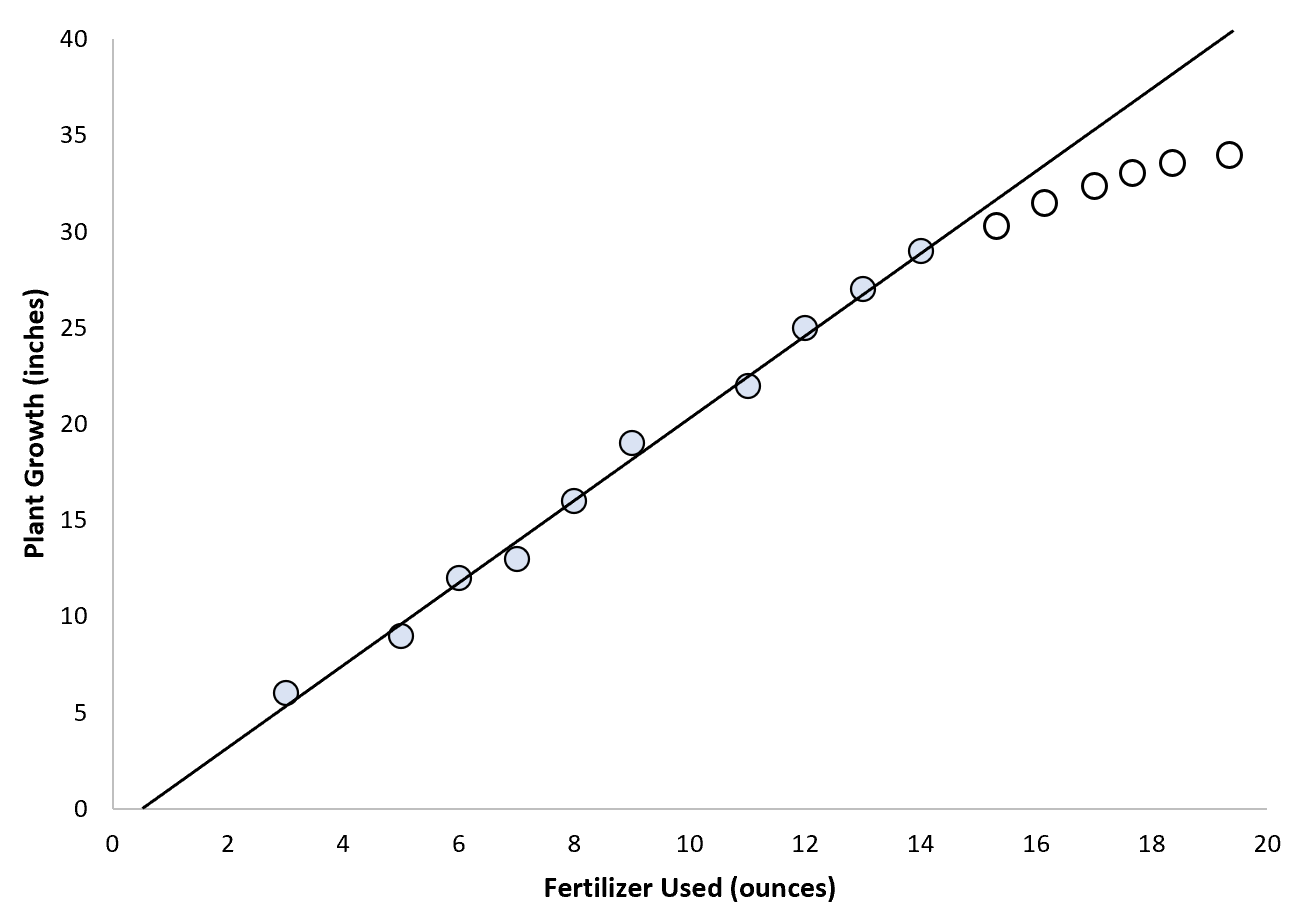
ဤအခြေအနေမျိုးတွင်၊ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏တန်ဖိုးများကို အပိုထုတ်နိုင်မှုအပေါ် ယုံကြည်မှုများစွာလျော့နည်းသွားနိုင်ပါသည်။

ယူဆောင်သွားခြင်း – Extrapolation သည် အခြားနေရာများထက် အချို့နေရာများတွင် ပိုအဓိပ္ပာယ်ရှိနိုင်သည်၊ သို့သော် မော်ဒယ်နှင့်ကိုက်ညီရန်အသုံးပြုသည့် တန်ဖိုးများအကွာအဝေးတွင်ရှိသော မော်ဒယ်သည် ကမ်းခြေအပြင်ဘက်တွင် မရှိသည့်အတွက် ဖြစ်နိုင်ခြေရှိသည့် အန္တရာယ်ရှိပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

Excel တွင် linear interpolation ပြုလုပ်နည်း
linear regression ဖြင့် ကြိုတင်ခန့်မှန်းနည်း