Interquartile အပိုင်းအခြား (သို့မဟုတ် interquartile အပိုင်းအခြား)

ဤဆောင်းပါးတွင် interquartile အကွာအဝေးကို interquartile အပိုင်းအခြားဟုလည်းသိကြသောအကွာအဝေးကိုရှင်းပြထားသည်။ တိကျသော ဥပမာတစ်ခုဖြင့် ကြားဖြတ်အကွာအဝေးကို မည်ကဲ့သို့ တွက်ချက်သည်ကို သင်လည်း တွေ့မြင်နိုင်မည်ဖြစ်ပါသည်။ ကြားကာလအပိုင်းအခြားနှင့် ကြားကာလကွာခြားချက်တို့ကို သင်လေ့လာနိုင်မည်ဖြစ်သည်။ ထို့အပြင်၊ သင်သည် online calculator ဖြင့် မည်သည့် data set ၏ interquartile range ကို တွက်ချက်နိုင်သည်။

interquartile (သို့မဟုတ် interquartile) အပိုင်းအခြားဆိုတာဘာလဲ။

interquartile အကွာအဝေး၊ interquartile အပိုင်းအခြားဟုလည်း ခေါ်သည်၊ သည် တတိယနှင့် ပထမ quartiles အကြား ခြားနားချက်ကို ညွှန်ပြသော ကိန်းဂဏန်းဆိုင်ရာ ကွဲလွဲမှုတိုင်းတာမှုတစ်ခုဖြစ်သည်။ ထို့ကြောင့်၊ ကိန်းဂဏန်းအချက်အလက်အစုတစ်ခု၏ interquartile အကွာအဝေးကို တွက်ချက်ရန်၊ တတိယနှင့် ပထမအကြိမ် quartiles ကို ဦးစွာရှာပြီးနောက် ၎င်းတို့ကို နုတ်ရပါမည်။

အတိုချုပ်အားဖြင့်၊ interquartile range ကို အတိုကောက် IQR ဖြင့် ဖော်ပြသည်။

interquartile range ၏ အားသာချက်အရှိဆုံးလက္ခဏာများထဲမှတစ်ခုမှာ ၎င်းသည် ခိုင်မာသောစာရင်းအင်းတစ်ခုဖြစ်ပြီး၊ ဆိုလိုသည်မှာ ၎င်းသည် outliers များအတွက် မြင့်မားသောကြံ့ခိုင်မှုရှိသည်။ interquartile အကွာအဝေးကို တွက်ချက်ရာတွင် လွန်ကဲသောတန်ဖိုးများကို ထည့်သွင်းစဉ်းစားမည်မဟုတ်သောကြောင့်၊ အထွက် အသစ်များပေါ်လာပါက ၎င်း၏တန်ဖိုးသည် အနည်းငယ်သာ ကွာခြားပါသည်။

ကွာတားအကွာအဝေးမှလွဲ၍ အခြားသော ကွဲလွဲမှုအတိုင်းအတာများ ထင်ရှားစွာရှိပါသည်၊ အထင်ရှားဆုံး မက်ထရစ်များမှာ အကွာအဝေး၊ ကွဲလွဲမှု၊ စံ (သို့မဟုတ်) စံသွေဖည်မှု၊ အဓိပ္ပာယ်သွေဖည်မှုနှင့် ကွဲလွဲမှု၏ကိန်းဂဏန်းများဖြစ်သည်။

interquartile (သို့မဟုတ် interquartile) အပိုင်းအခြားကို တွက်ချက်နည်း

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ ဒေတာအစုတစ်ခု၏ interquartile အကွာအဝေး (သို့မဟုတ် interquartile အကွာအဝေး) ကိုတွက်ချက်ရန်၊ သင်သည် ဒေတာအစု၏ ပထမနှင့် တတိယမြောက် quartile ကို ဦးစွာရှာရမည်ဖြစ်ပြီး၊ ထို့နောက် တတိယအကြိမ်၏အနုတ်ကို ပထမအကြိမ်အနုတ်ကို တွက်ချက်ရပါမည်။

ထို့ကြောင့် interquartile range သို့မဟုတ် interquartile range ကို တွက်ချက်ရန် ဖော်မြူလာမှာ-

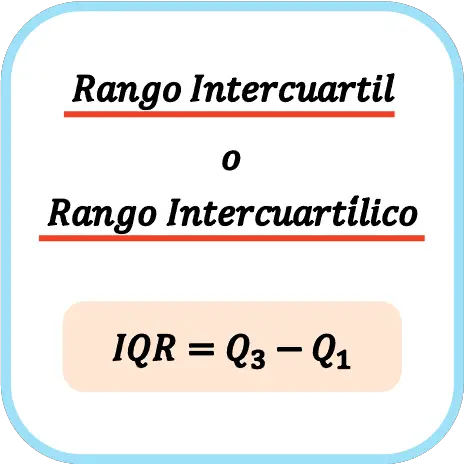
👉 မည်သည့်ဒေတာအစုံအတွက်မဆို interquartile range ကိုတွက်ချက်ရန် အောက်ပါ calculator ကိုသုံးနိုင်သည်။

ထို့ကြောင့်၊ ကိန်းဂဏန်းနမူနာတစ်ခု၏ လေးပုံတစ်ပုံကို တွက်ချက်ပုံကို သိထားရန် လိုအပ်ပါသည်။ ထို့ကြောင့် အောက်ပါဆောင်းပါးကို ဆက်လက်မလုပ်ဆောင်မီ ရှင်းလင်းချက်နှင့် ဆက်လက်လုပ်ဆောင်ရန် အကြံပြုအပ်ပါသည်။

interquartile (သို့မဟုတ် interquartile) အပိုင်းအခြား၏ ဥပမာ

အောက်တွင်ဖော်ပြထားသော interquartile range (သို့မဟုတ် interquartile range) အတွက် အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ပုံသေနည်းသည် ဖြေရှင်းထားသော လေ့ကျင့်ခန်းတစ်ခုဖြစ်ပြီး ဤပြန့်ကျဲမှုတိုင်းတာမှုအမျိုးအစားကို မည်ကဲ့သို့ တွက်ချက်သည်ကို အတိအကျသိနိုင်မည်ဖြစ်သည်။

• ကုမ္ပဏီတစ်ခုတွင် ရင်းနှီးမြုပ်နှံရန် စိတ်ကူးကောင်းရှိမရှိ ကိန်းဂဏန်းများကို ခွဲခြမ်းစိတ်ဖြာလိုပါသည်။ ဒါကိုလုပ်ဖို့၊ ပြီးခဲ့တဲ့ 15 လအတွင်း ဒီကုမ္ပဏီရဲ့ စတော့စျေးနှုန်းဆိုင်ရာ အချက်အလက်တွေကို စုဆောင်းခဲ့ပါတယ်။ အောက်ပါဇယားတွင် အနိမ့်ဆုံးမှ အမြင့်ဆုံးသို့ စီထားသော လေ့လာတွေ့ရှိထားသော အချက်အလက်များကို သင်တွေ့မြင်နိုင်ပါသည်။ ဤဒေတာအတွဲအတွက် ကွာတားအကွာအဝေးကို တွက်ချက်ပါ။

ယခင်အပိုင်းတွင်ကျွန်ုပ်တို့မြင်ခဲ့သည့်အတိုင်း၊ နမူနာ၏ interquartile အကွာအဝေး (သို့မဟုတ် interquartile အကွာအဝေး) ကိုရရှိရန်ကျွန်ုပ်တို့သည်ပထမနှင့်တတိယအကြိမ်များကိုတွက်ချက်ရပါမည်။

ပထမ quartile သည် ယူရို 8.95/share နှင့် သက်ဆိုင်သည့် တန်ဖိုးများ၏ ပထမတစ်ဝက်၏ ပျမ်းမျှဖြစ်သည်။

အခြားတစ်ဖက်တွင်၊ တတိယ quartile သည် တန်ဖိုးများ၏ ဒုတိယနှစ်ဝက်၏ အလယ်အလတ်တန်ဖိုးဖြစ်သည်၊ ထို့ကြောင့် ယူရို 9.83/share ဖြစ်သည်။

ထို့ကြောင့် interquartile အပိုင်းအခြားကို ရှာရန်၊ ရိုးရိုးလေး ဖော်မြူလာကို အသုံးချပြီး တတိယ quartile ကို နုတ်ပြီး ပထမ quartile ကို နုတ်ပါ။

Interquartile (သို့မဟုတ် Interquartile) Range Calculator

၎င်း၏ ကွာတားအကွာအဝေး သို့မဟုတ် ကွာတားအကွာအဝေးကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်တွင် သတ်မှတ်ကိန်းဂဏန်း အချက်အလက်ကို ထည့်သွင်းပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

Interquartile Range နှင့် Range ကွာခြားချက်

စာရင်းဇယားများတွင်၊ ကြားကာလအပိုင်းအခြား (သို့မဟုတ် interquartile အကွာအဝေး) နှင့်ကြားကာလအကြားခြားနားချက် သည်တွက်ချက်မှုလုပ်ဆောင်ရန်ယူထားသောတန်ဖိုးများဖြစ်သည်။ interquartile အပိုင်းအခြားသည် တတိယနှင့် ပထမ quartiles အကြား ခြားနားချက်ဖြစ်ပြီး အကွာအဝေးသည် နမူနာ၏ လွန်ကဲတန်ဖိုးများအကြား ကွာခြားချက်ဖြစ်သည်။

ထို့ကြောင့် ကြားကာလအပိုင်းအခြားသည် ဗဟိုဒေတာကို အသုံးပြု၍ နမူနာတစ်ခု၏ ပျံ့နှံ့မှုကို တိုင်းတာပြီး ကြားကာလသည် လွန်ကဲသောဒေတာကို အသုံးပြု၍ နမူနာ၏ပျံ့နှံ့မှုကို တိုင်းတာသည်။

ထို့ကြောင့်၊ ၎င်းတို့သည် ဒေတာအစု၏ အနိမ့်ဆုံး သို့မဟုတ် အများဆုံးကို ကိုယ်စားပြုသောကြောင့် ကိန်းဂဏန်းအကွာအဝေးသည် အကြမ်းဖျင်းအား ဖြင့် များစွာသက်ရောက်မှုရှိသည်။ ထို့ကြောင့် interquartile range ၏ အားသာချက်များထဲမှ တစ်ခုက ၎င်းသည် ပိုမိုကြံ့ခိုင်မှုရှိခြင်းပင်ဖြစ်သည်။

interquartile (သို့မဟုတ် interquartile) အကွာအဝေးကို ဘာအတွက်သုံးတာလဲ။

အဓိကအားဖြင့်၊ ကွာတားအကွာအဝေး (သို့မဟုတ် ကွာတားအကွာအဝေး) ကို ဒေတာအစုတစ်ခု၏ ဖြန့်ဖြူးမှုကို တိုင်းတာရန် အသုံးပြုသည် ။ နမူနာတစ်ခု၏ ပြန့်ကျဲမှုကို ခွဲခြမ်းစိတ်ဖြာခြင်း အပြည့်အဝ ကိန်းဂဏန်းဆိုင်ရာ အစီအမံများကို တွက်ချက်ရန် လိုအပ်သော်လည်း၊ interquartile အကွာအဝေးသည် နမူနာအား မည်မျှ ပြန့်ကျဲစေသည်၊ အနည်းဆုံး ဗဟိုတန်ဖိုးများကို ပေးဆောင်သည် ။

ထို့ကြောင့် interquartile range ၏အဓိပ္ပာယ်ဖွင့်ဆိုချက်သည် အတော်လေးရိုးရှင်းပါသည်။ interquartile အကွာအဝေး၏တန်ဖိုးပိုမိုမြင့်မားလေ၊ အလယ်ဒေတာသည်နမူနာတွင်ပိုမိုပြန့်နှံ့လေလေ၊ နှင့် interquartile အကွာအဝေးငယ်လေလေ၊ အလယ်အလတ်ဒေတာများသည် အတူတကွပိုမိုနီးကပ်လေလေဖြစ်သည်။

ထို့အပြင်၊ interquartile range သည် စတော့ဈေးကွက်ရှိ စတော့ဈေးကွက်တွင် စတော့စျေးနှုန်းအပြုအမူကို ပိုင်းခြားစိတ်ဖြာရန် တွင်ကျယ်စွာသုံးသော ပုံးကွက်နှင့် ပါးသိုင်းကွက်တစ်ခုကို ဖန်တီးရန်အတွက်လည်း အသုံးဝင်ပါသည်။