Interquartile range (iqr) သည် outliers ကြောင့် ထိခိုက်ပါသလား။

စာရင်းဇယားများတွင်၊ ဖြန့်ဖြူးမှုတစ်ခုတွင် တန်ဖိုးများ မည်မျှကျယ်ပြန့်သည်ကို ကျွန်ုပ်တို့ သိလိုကြသည်။

ပျံ့နှံ့မှုကို တိုင်းတာရန် ရေပန်းစားသောနည်းလမ်းမှာ ဒေတာအစုတစ်ခု၏ ပထမ quartile နှင့် တတိယ quartile အကြားခြားနားချက်အဖြစ် တွက်ချက်ထားသည့် interquartile range ဖြစ်သည်။ Quartiles များသည် data set တစ်ခုကို လေးပိုင်းအညီအမျှခွဲပေးသော ရိုးရှင်းသောတန်ဖိုးများဖြစ်သည်။

ဥပမာ- interquartile အပိုင်းအခြားကို တွက်ချက်ခြင်း။

အောက်ပါဥပမာသည် ပေးထားသောဒေတာအတွဲအတွက် interquartile အကွာအဝေးကို တွက်ချက်နည်းကို ပြသည်-

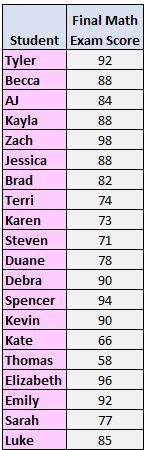
အဆင့် 1: တန်ဖိုးများကို အသေးဆုံးမှ အကြီးဆုံးသို့ စီစဉ်ပါ။

၅၈၊ ၆၆၊ ၇၁၊ ၇၃၊ ၇၄၊ ၇၇၊ ၇၈၊ ၈၂၊ ၈၄၊ ၈၅၊ ၈၈၊ ၈၈၊ ၈၈၊ ၉၀၊ ၉၀၊ ၉၂၊ ၉၂၊ ၉၄၊ ၉၆၊ ၉၈၊

2. ပျမ်းမျှကိုရှာပါ။

၅၈၊ ၆၆၊ ၇၁၊ ၇၃၊ ၇၄၊ ၇၇၊ ၇၈၊ ၈၂၊ ၈၄၊ ၈၅၊ ၈၈၊ ၈၈၊ ၈၈၊ ၉၀၊ ၉၀၊ ၉၂၊ ၉၂၊ ၉၄၊ ၉၆၊ ၉၈

ဤအခြေအနေတွင် ပျမ်းမျှသည် 85 နှင့် 88 ကြားဖြစ်သည်။

3. အလယ်အလတ်သည် သတ်မှတ်ဒေတာကို နှစ်ပိုင်းခွဲသည်။ အောက်ပိုင်း၏ အလယ်ဗဟိုသည် အောက်ပိုင်း quartile ဖြစ်ပြီး အထက်ပိုင်း၏ အလယ်တန်းသည် အထက် quartile ဖြစ်သည်။

၅၈၊ ၆၆၊ ၇၁၊ ၇၃၊ ၇၄၊ ၇၇၊ ၇၈၊ ၈၂၊ ၈၄၊ ၈၅၊ ၈၈၊ ၈၈၊ ၈၈၊ ၉၀၊ ၉၀၊ ၉၂၊ ၉၂၊ ၉၄၊ ၉၆၊ ၉၈

4. interquartile အပိုင်းအခြားကို တွက်ချက်ပါ။

ဤကိစ္စတွင်၊ ပထမ quartile သည် data set ၏ အောက်ခြေတစ်ဝက်ရှိ အလယ်နှစ်တန်ဖိုး၏ ပျမ်းမျှ (75.5) ဖြစ်ပြီး တတိယ quartile သည် set data ၏ ထိပ်ဆုံးတစ်ဝက်ရှိ အလယ်တန်းနှစ်ခု၏ ပျမ်းမျှတန်ဖိုးဖြစ်သည် (၉၁)။

ထို့ကြောင့် interquartile range သည် 91 – 75.5 = 15.5 ဖြစ်သည်။

Interquartile range သည် outliers များကြောင့် မထိခိုက်ပါ။

ဒေတာအစုတစ်ခု၏ “ ပျံ့နှံ့မှု” ကို တွက်ချက်ရာတွင် လူတို့သည် ကြားပိုင်းအကွာအဝေး (IQR) ကို အသုံးပြုလိုသည့် အကြောင်းရင်းတစ်ခုမှာ ၎င်းသည် အစွန်းထွက်သူများအတွက် အားကောင်းသောကြောင့်ဖြစ်သည်။ IQR သည် ဒေတာတန်ဖိုးများ၏ အလယ်အလတ် 50% အကွာအဝေးဖြစ်သောကြောင့်၊ ၎င်းသည် လွန်ကဲသော outliers များ ကြောင့် သက်ရောက်မှုမရှိပါ။

ယင်းကို သရုပ်ပြရန်၊ အောက်ပါဒေတာအတွဲကို ထည့်သွင်းစဉ်းစားပါ။

[၁၊ ၄၊ ၈၊ ၁၁၊ ၁၃၊ ၁၇၊ ၁၇၊ ၂၀]

ဤဒေတာအတွဲအတွက် မတူညီသော ပြန့်ပွားမှုမက်ထရစ်များသည် အောက်ပါအတိုင်းဖြစ်သည်-

• Interquartile အပိုင်းအခြား- ၁၁
• အပိုင်း- ၁၉
• စံသွေဖည်: 6.26
• ကွာခြားချက်- ၃၉.၂၃

ယခု တူညီသော ဒေတာအတွဲကို ထည့်သွင်းစဉ်းစားသော်လည်း လွန်ကဲသော အစွန်းထွက်တစ်ခုဖြင့် ထည့်သွင်းစဉ်းစားပါ။

[၁၊ ၄၊ ၈၊ ၁၁၊ ၁၃၊ ၁၇၊ ၁၇၊ ၂၀၊ ၁၅၀ ]

ဤဒေတာအတွဲအတွက် မတူညီသော ပြန့်ပွားမှုမက်ထရစ်များသည် အောက်ပါအတိုင်းဖြစ်သည်-

• Interquartile အပိုင်းအခြား- 12.5
• အပိုင်းအခြား- ၁၄၉
• စံသွေဖည်: 43.96
• ပျံ့နှံ့မှု- 1,932.84

interquartile အပိုင်းအခြားသည် 11 မှ 12.5 သို့ အနည်းငယ်ပြောင်းလဲသွားသည်ကို သတိပြုပါ။ သို့သော်လည်း အခြားသော ပြန့်ကျဲမှု အတိုင်းအတာအားလုံး သိသိသာသာ ပြောင်းလဲသွားသည်။

၎င်းသည် အခြားသော ကွဲကွာနေသော အတိုင်းအတာများကဲ့သို့ ကွာတားအကွာအဝေးကြား အကွာအဝေးကို သက်ရောက်မှုမရှိကြောင်း ပြသသည်။ ဤအကြောင်းကြောင့်၊ မည်သည့်ဖြန့်ဖြူးမှုတွင်မဆို အလယ်တန်းတန်ဖိုးများ၏ 50% ၏ဖြန့်ဖြူးမှုကို တိုင်းတာရန် ယုံကြည်စိတ်ချရသောနည်းလမ်းဖြစ်သည်။

နောက်ထပ်ဖတ်ရန်:

ပြန့်ကျဲမှုတိုင်းတာမှုများ
Interquartile Range ဂဏန်းတွက်စက်