Intraclass ဆက်စပ်ဆက်စပ်ကိန်း- အဓိပ္ပါယ် + ဥပမာ

အဆင့်သတ်မှတ်သူ နှစ်ဦး သို့မဟုတ် ထို့ထက်ပိုသော လေ့လာမှုများတွင် ရမှတ်များ၏ ယုံကြည်စိတ်ချရမှုကို တိုင်းတာရန်အတွက် အတန်းတွင်းဆက်စပ်ဆက်စပ်ကိန်း (ICC) ကို အသုံးပြုသည်။

ICC ၏တန်ဖိုးသည် 0 မှ 1 အထိရှိနိုင်ပြီး 0 သည် အဆင့်သတ်မှတ်သူများကြားတွင် ယုံကြည်စိတ်ချရမှုမရှိကြောင်း နှင့် 1 သည် အဆင့်သတ်မှတ်သူများကြားတွင် ပြီးပြည့်စုံသောယုံကြည်စိတ်ချရမှုကို ညွှန်ပြသည့် 0 ဖြစ်သည်။

ရိုးရိုးရှင်းရှင်းပြောရလျှင်၊ မတူညီသော အဆင့်သတ်မှတ်သူများမှ အကြောင်းအရာများ (သို့မဟုတ် အကြောင်းအရာများ) ကို ယုံကြည်စိတ်ချစွာ အဆင့်သတ်မှတ်နိုင်သည်ဆိုသည်ကို ဆုံးဖြတ်ရန် ICC ကို အသုံးပြုပါသည်။

အောက်ပါအချက်သုံးချက်အပေါ် မူတည်၍ တွက်ချက်နိုင်သော ICC ၏ မတူညီသော ဗားရှင်းများစွာ ရှိပါသည်။

• မော်ဒယ်- တစ်လမ်းသွား ကျပန်းအကျိုးသက်ရောက်မှုများ၊ နှစ်လမ်းကျပန်းအကျိုးသက်ရောက်မှုများ သို့မဟုတ် နှစ်လမ်းသွား ရောနှောထားသော အကျိုးဆက်များ
• ဆက်ဆံရေးအမျိုးအစား- ညီညွတ်မှု သို့မဟုတ် အကြွင်းမဲ့သဘောတူညီချက်
• ယူနစ်- အဆင့် သတ်မှတ်သူ တစ်ဦးတည်း သို့မဟုတ် ပျမ်းမျှ အဆင့်သတ်မှတ်သူများ

ဤသည်မှာ မတူညီသော မော်ဒယ် သုံးမျိုး၏ အကျဉ်းချုပ် ဖော်ပြချက်ဖြစ်ပါသည်။

1. တစ်လမ်းမောင်းကျပန်းအကျိုးသက်ရောက်မှုပုံစံ- ဤပုံစံသည် ဘာသာရပ်တစ်ခုစီကို ကျပန်းရွေးချယ်ထားသော အကဲဖြတ်သူများ၏ မတူညီသောအုပ်စုတစ်စုမှ အကဲဖြတ်သည်ဟု ယူဆပါသည်။ ဤပုံစံဖြင့်၊ အဆင့်သတ်မှတ်သူများကို ကျပန်းအကျိုးသက်ရောက်မှုများ၏ရင်းမြစ်အဖြစ် သတ်မှတ်သည်။ ဘာသာရပ်တစ်ခုစီကို အကဲဖြတ်ရန် ယေဘုယျအားဖြင့် တူညီသောအကဲဖြတ်အဖွဲ့ကို အသုံးပြုထားသောကြောင့် ဤပုံစံကို လက်တွေ့တွင် အသုံးပြုခဲပါသည်။

2. နှစ်လမ်းကျပန်းအကျိုးသက်ရောက်မှုပုံစံ- ဤပုံစံသည် အဆင့်သတ်မှတ်ထားသော k အုပ်စုတစ်စုကို လူဦးရေတစ်ခုမှ ကျပန်းရွေးချယ်ပြီး ဘာသာရပ်များကို အဆင့်သတ်မှတ်ရန် အသုံးပြုသည်ဟု ယူဆသည်။ ဤပုံစံကိုအသုံးပြုခြင်း၊ အဆင့်သတ်မှတ်ခြင်းနှင့် ဘာသာရပ်များကို ကျပန်းအကျိုးသက်ရောက်မှုများ၏ရင်းမြစ်များအဖြစ် သတ်မှတ်သည်။ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏ရလဒ်များကို လေ့လာမှုတွင်အသုံးပြုသည့် အလားတူအဆင့်သတ်မှတ်မှုများနှင့် ယေဘုယျဖော်ပြလိုသည့်အခါ ဤပုံစံကို မကြာခဏအသုံးပြုပါသည်။

3. နှစ်လမ်းရောစပ်သောအကျိုးသက်ရောက်မှုပုံစံ- ဤပုံစံသည် အဆင့်သတ်မှတ်ခြင်း k အုပ်စုတစ်စုအား လူဦးရေမှ ကျပန်းရွေးချယ်ပြီး ဘာသာရပ်များကို အဆင့်သတ်မှတ်ရန် အသုံးပြုသည်ဟုလည်း ယူဆပါသည်။ သို့သော်၊ ကျွန်ုပ်တို့ရွေးချယ်ထားသော အဆင့်သတ်မှတ်ပေးသူများအုပ်စုသည် တစ်ခုတည်းသော စိတ်ဝင်စားဖွယ်အဆင့်သတ်မှတ်သူများသာဖြစ်သည်ဟု ယူဆသည်၊ ဆိုလိုသည်မှာ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏ရလဒ်များကို လေ့လာမှုတွင်အသုံးပြုသည့် အဆင့်သတ်မှတ်သူများနှင့် အလားတူသွင်ပြင်လက္ခဏာများတူညီသော အခြားအဆင့်သတ်မှတ်သူများထံသို့ ကျွန်ုပ်တို့၏ရလဒ်များကို ယေဘုယျဖော်ပြလိုခြင်းမရှိကြောင်း ဆိုလိုပါသည်။

ဤသည်မှာ ကျွန်ုပ်တို့တိုင်းတာလိုသော မတူညီသော ဆက်ဆံရေး နှစ်မျိုး၏ အကျဉ်းချုပ်ဖော်ပြချက်ဖြစ်သည်-

1. ညီညွတ်မှု- တရားသူကြီးများ၏ အဆင့်သတ်မှတ်ချက်များကြား စနစ်ကျသော ကွာခြားချက်များကို ကျွန်ုပ်တို့ စိတ်ဝင်စားပါသည် (ဥပမာ၊ တရားသူကြီးများသည် အလားတူအကြောင်းအရာများကို အနိမ့်နှင့် မြင့်သည်ဟု အဆင့်သတ်မှတ်ခဲ့ပါသလား။)

2. အကြွင်းမဲ့သဘောတူညီချက်- တရားသူကြီးများ၏ ရမှတ်များအကြား အကြွင်းမဲ့ ကွာခြားချက်များကို ကျွန်ုပ်တို့ စိတ်ဝင်စားပါသည် (ဥပမာ၊ တရားသူကြီး A နှင့် တရားသူကြီး B တို့၏ ရမှတ်များအကြား လုံးဝကွာခြားချက်ကား အဘယ်နည်း။)

ဤသည်မှာ ကျွန်ုပ်တို့စိတ်ဝင်စားနိုင်သည့် မတူညီသော ယူနစ် နှစ်ခု၏ အကျဉ်းချုပ်ဖော်ပြချက်ဖြစ်သည်-

1. တစ်ဦးတည်းသုံးသပ်သူ- ကျွန်ုပ်တို့သည် တိုင်းတာမှုအတွက် အခြေခံအဖြစ် တစ်ဦးတည်းသုံးသပ်သူ၏ အဆင့်သတ်မှတ်ချက်များကိုသာ အသုံးပြုလိုပါသည်။

2. အဆင့်သတ်မှတ်ခြင်း- ကျွန်ုပ်တို့သည် တိုင်းတာခြင်းအတွက် အခြေခံအဖြစ် တရားသူကြီးများ၏ ရမှတ်အားလုံး၏ ပျမ်းမျှအား အသုံးပြုလိုပါသည်။

မှတ်ချက်- အကြောင်းအရာ တစ်ခုစီကို လွဲချော်နေသော အဆင့်သတ်မှတ်သူနှစ်ဦးကြားတွင် သဘောတူညီချက်အဆင့်ကို တိုင်းတာလိုပါက၊ Cohen’s Kappa အစား သင်အသုံးပြုသင့်သည်။

intraclass correlation coefficient ကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။

Koo & Li ၏ အဆိုအရ intraclass correlation coefficient ၏တန်ဖိုးကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုရမည်နည်း

• 0.50 အောက်- ယုံကြည်စိတ်ချရမှု ညံ့ဖျင်းသည်။
• 0.5 နှင့် 0.75 ကြား- အလယ်အလတ် ယုံကြည်စိတ်ချရမှု
• 0.75 နှင့် 0.9 ကြား- ယုံကြည်စိတ်ချရမှုကောင်းသည်။
• 0.9 ထက်ကြီးသည်- အလွန်ကောင်းမွန်သော ယုံကြည်စိတ်ချရမှု

အောက်ဖော်ပြပါ ဥပမာသည် လက်တွေ့တွင် intraclass ဆက်စပ်ဆက်စပ်ကိန်းကို တွက်ချက်နည်းကို ပြသထားသည်။

ဥပမာ- intraclass ဆက်စပ်ဆက်စပ်ကိန်းကို တွက်ချက်ခြင်း။

မတူညီသော ကောလိပ်ဝင်ခွင့်စာမေးပွဲ ၁၀ ခု၏ အရည်အသွေးကို အကဲဖြတ်ရန် မတူညီသော တရားသူကြီးလေးဦးကို တောင်းဆိုသည်ဆိုပါစို့။ ရလဒ်များကို အောက်တွင် ပြထားသည်။

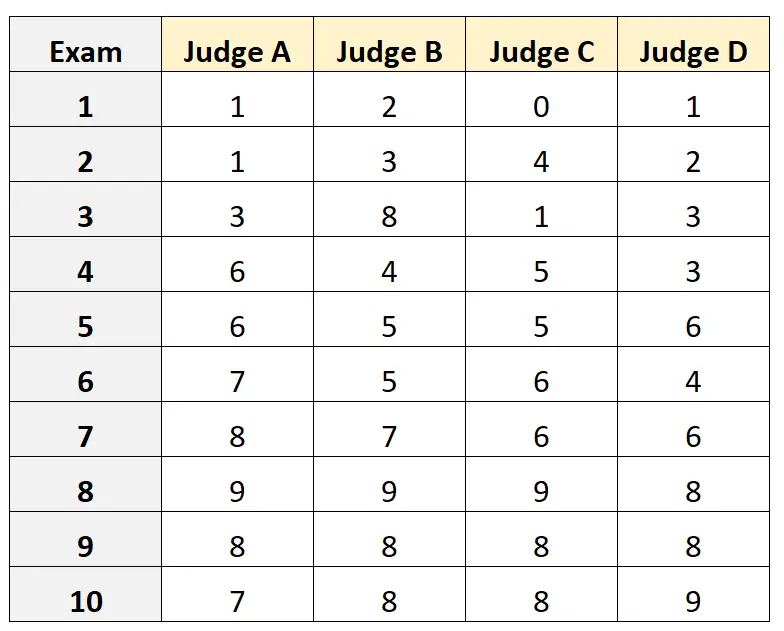
ဝင်ခွင့်စာမေးပွဲအတွက် အရည်အချင်းပြည့်မီသော တရားသူကြီးများထဲမှ တရားသူကြီးလေးဦးကို ကျပန်းရွေးချယ်ပြီး တရားသူကြီးများအကြား အကြွင်းမဲ့သဘောတူညီချက်ကို တိုင်းတာလိုပြီး ကျွန်ုပ်တို့၏တိုင်းတာမှု၏အခြေခံအဖြစ် အကဲဖြတ်သူတစ်ဦးတည်း၏ရှုထောင့်မှ ရမှတ်များကို အသုံးပြုလိုသည်ဆိုပါစို့။

R တွင်အောက်ပါကုဒ်ကိုအသုံးပြု၍ နှစ်လမ်းကျပန်းအကျိုးသက်ရောက်မှုပုံစံ တစ်ခုနှင့်ကိုက်ညီရန်၊ အကြွင်းမဲ့သဘောတူညီချက် အဖြစ် အဆင့်သတ်မှတ်သူများကြားဆက်ဆံရေးအဖြစ်နှင့် တစ်ခုတည်း ယူနစ်ကို စိတ်ဝင်စားမှုယူနစ်အဖြစ်အသုံးပြုခြင်းတို့ကိုအသုံးပြု၍ ကျွန်ုပ်တို့အသုံးပြုနိုင်သည်-

 #load the interrater reliability package
library (irr)

#define data
data <- data. frame (A=c(1, 1, 3, 6, 6, 7, 8, 9, 8, 7),
                   B=c(2, 3, 8, 4, 5, 5, 7, 9, 8, 8),
                   C=c(0, 4, 1, 5, 5, 6, 6, 9, 8, 8),
                   D=c(1, 2, 3, 3, 6, 4, 6, 8, 8, 9))

#calculate ICC
icc(data, model = " twoway ", type = " agreement ", unit = " single ")

   Model: twoway 
   Type: agreement 

   Subjects = 10 
     Failures = 4 
   ICC(A,1) = 0.782

 F-Test, H0: r0 = 0; H1: r0 > 0 
    F(9.30) = 15.3, p = 5.93e-09 

 95%-Confidence Interval for ICC Population Values:
  0.554 < ICC < 0.931

intraclass correlation coefficient (ICC) သည် 0.782 ဖြစ်သည် ။

ICC ကို ဘာသာပြန်ခြင်းအတွက် လက်မ၏ စည်းမျဉ်းများကို အခြေခံ၍ 0.782 ရှိသော ICC သည် စာမေးပွဲများကို အဆင့်သတ်မှတ်သူများမှ “ ကောင်းမွန်သော” ယုံကြည်စိတ်ချရမှုဖြင့် ရမှတ်ရနိုင်ကြောင်း ကျွန်ုပ်တို့ ကောက်ချက်ချနိုင်ပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် မတူညီသော စာရင်းအင်းဆော့ဖ်ဝဲများတွင် ICC တွက်ချက်နည်းကို အသေးစိတ်ရှင်းပြပေးသည်-

Excel တွင် Intraclass Correlation Coefficient တွက်ချက်နည်း
R တွင် intraclass correlation coefficient တွက်ချက်နည်း
Python တွင် Intraclass Correlation Coefficient တွက်ချက်နည်း