Python တွင် k-means clustering- step-by-step ဥပမာ

machine learning တွင် အသုံးအများဆုံး အစုလိုက်အပြုံလိုက် အယ်လဂိုရီသမ်များထဲမှ တစ်ခုကို k-means အစုအဝေးပြုလုပ်ခြင်း ဟုခေါ်သည်။

K ဆိုသည်မှာ အစုအဝေးတစ်ခုစီကို K အစုအဝေးတစ်ခုသို့ ဒေတာအတွဲတစ်ခုမှ စူးစမ်းလေ့လာမှုတစ်ခုစီကို ထားရှိပေးသည့် နည်းလမ်းတစ်ခုဖြစ်သည်။

အဆုံးပန်းတိုင်မှာ အစုအဝေးတစ်ခုစီရှိ ရှုမြင်သုံးသပ်ချက်များသည် တစ်ခုနှင့်တစ်ခု အလွန်တူညီပြီး ကွဲပြားသောအစုအဝေးများတွင် လေ့လာမှုများသည် တစ်ခုနှင့်တစ်ခု အလွန်ကွာခြားသော်လည်း K အစုအဝေးများ ရှိရန်ဖြစ်သည်။

လက်တွေ့တွင်၊ ကျွန်ုပ်တို့သည် K-Means အစုအဝေးပြုလုပ်ရန် အောက်ပါအဆင့်များကို အသုံးပြုသည်-

1. K အတွက် တန်ဖိုးတစ်ခုကို ရွေးပါ။

• ပထမဦးစွာ၊ ကျွန်ုပ်တို့သည် ဒေတာတွင် ကျွန်ုပ်တို့သတ်မှတ်လိုသည့် အစုအဝေးမည်မျှရှိသည်ကို ဆုံးဖြတ်ရန် လိုအပ်သည်။ မကြာခဏဆိုသလို ကျွန်ုပ်တို့သည် K အတွက် မတူညီသောတန်ဖိုးများစွာကို စမ်းသပ်ပြီး ပေးထားသည့်ပြဿနာအတွက် အသင့်လျော်ဆုံးဖြစ်ပုံရသည့် အစုအဝေးအရေအတွက်ကို သိရှိနိုင်ရန် ရလဒ်များကို ခွဲခြမ်းစိတ်ဖြာရန် လိုအပ်ပါသည်။

2. စောင့်ကြည့်မှုတစ်ခုစီကို 1 မှ K မှ ကနဦးအစုအဝေးတစ်ခုသို့ ကျပန်းသတ်မှတ်ပါ။

3. အစုအဖွဲ့တာဝန်များ မပြောင်းလဲမချင်း အောက်ပါလုပ်ငန်းစဉ်များကို လုပ်ဆောင်ပါ။

• K အစုအဝေးတစ်ခုစီအတွက်၊ အစုအဝေး၏ ဆွဲငင်အားဗဟိုကို တွက်ချက်ပါ။ ဤသည်မှာ kth အစုအဝေး၏ လေ့လာတွေ့ရှိချက်များအတွက် p- mean features ၏ vector မျှသာဖြစ်သည်။
• စောင့်ကြည့်မှုတစ်ခုစီကို အနီးစပ်ဆုံး အလယ်ဗဟိုဖြင့် အစုအဝေးသို့ သတ်မှတ်ပေးပါ။ ဤတွင်၊ အနီးစပ်ဆုံး ကို Euclidean အကွာအဝေးကို အသုံးပြု၍ သတ်မှတ်သည်။

အောက်ပါ အဆင့်ဆင့် ဥပမာသည် sklearn module မှ KMeans လုပ်ဆောင်ချက်ကို အသုံးပြု၍ Python တွင် k-means အစုအဝေးကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသထားသည်။

အဆင့် 1: လိုအပ်သော module များကိုတင်သွင်းပါ။

ဦးစွာ၊ ကျွန်ုပ်တို့သည် k-means အစုအဝေးပြုလုပ်ရန် လိုအပ်မည့် module အားလုံးကို တင်သွင်းပါမည်-

 import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler

အဆင့် 2: DataFrame ကိုဖန်တီးပါ။

ထို့နောက်၊ မတူညီသော ဘတ်စကက်ဘောကစားသမား 20 အတွက် အောက်ပါ variable သုံးခုပါဝင်သော DataFrame တစ်ခုကို ဖန်တီးပါမည်။

• အမှတ်များ
• ကူညီကြပါ
• ခုန်ပေါက်သည်။

အောက်ပါ ကုဒ်သည် ဤပန်ဒါ DataFrame ဖန်တီးပုံကို ပြသသည် ။

 #createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
                              35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
                   ' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
                               np.nan, 9, 4, 3, 4, 12, 15, 11],
                   ' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
                                11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})

#view first five rows of DataFrame
print ( df.head ())

   points assists rebounds
0 18.0 3.0 15
1 NaN 3.0 14
2 19.0 4.0 14
3 14.0 5.0 10
4 14.0 4.0 8

ဤမက်ထရစ်သုံးခုအပေါ် အခြေခံ၍ အလားတူသရုပ်ဆောင်များကို အုပ်စုဖွဲ့ရန် k-Means ကို အသုံးပြုပါမည်။

အဆင့် 3- DataFrame ကို ရှင်းလင်းပြီး ပြင်ဆင်ပါ။

ထို့နောက် အောက်ပါအဆင့်များကို လုပ်ဆောင်ပါမည်။

• မည်သည့်ကော်လံတွင်မဆို NaN တန်ဖိုးများပါသည့် အတန်းများကို ချရန် dropna() ကို သုံးပါ။
• 0 mean နှင့် 1 ၏ စံသွေဖည်မှုရှိရန် variable တစ်ခုစီကို StandardScaler() ကိုသုံးပါ။

အောက်ပါကုဒ်သည် ၎င်းကိုပြုလုပ်နည်းကို ပြသသည်-

 #drop rows with NA values in any columns
df = df. dropna ()

#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)

#view first five rows of scaled DataFrame
print (scaled_df[:5])

[[-0.86660275 -1.22683918 1.72722524]
 [-0.72081911 -0.96077767 1.45687694]
 [-1.44973731 -0.69471616 0.37548375]
 [-1.44973731 -0.96077767 -0.16521285]
 [-1.88708823 -0.16259314 1.45687694]]

မှတ်ချက် – k-means algorithm နှင့် ကိုက်ညီသောအခါတွင် ကိန်းရှင်တစ်ခုစီသည် တူညီသောအရေးပါမှု ရှိစေရန် ကျွန်ုပ်တို့ အတိုင်းအတာကို အသုံးပြုပါသည်။ မဟုတ်ပါက၊ အကျယ်ပြန့်ဆုံးသော ကိန်းရှင်များသည် သြဇာလွှမ်းမိုးမှု လွန်ကဲနေပေလိမ့်မည်။

အဆင့် 4- အကောင်းဆုံး အစုအဝေးအရေအတွက်ကို ရှာပါ။

Python တွင် k-means အစုအဝေးကို လုပ်ဆောင်ရန်၊ ကျွန်ုပ်တို့သည် sklearn module မှ KMeans လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်သည်။

ဤလုပ်ဆောင်ချက်သည် အောက်ပါအခြေခံ syntax ကိုအသုံးပြုသည်-

KMeans(init=’random’၊ n_clusters=8၊ n_init=10၊ random_state=None)

ရွှေ-

• init- က နဦးနည်းပညာကို ထိန်းချုပ်သည်။
• n_clusters : လေ့လာတွေ့ရှိချက်များကို နေရာချရန် အစုအဝေးအရေအတွက်။
• n_init : လုပ်ဆောင်ရန် ကနဦးလုပ်ဆောင်မှု အရေအတွက်။ မူရင်းမှာ k-means algorithm ကို 10 ကြိမ် run ပြီး အနိမ့်ဆုံး SSE ဖြင့် ပြန်ပေးခြင်းဖြစ်သည်။
• Random_state : algorithm ရလဒ်များကို ပြန်ထုတ်ပေးရန် သင်ရွေးချယ်နိုင်သော ကိန်းပြည့်တန်ဖိုးတစ်ခု။

ဤလုပ်ဆောင်ချက်အတွက် အရေးကြီးဆုံး အကြောင်းပြချက်မှာ n_clusters ဖြစ်သည်၊ ၎င်းသည် အစုလိုက်အပြုံလိုက်မည်မျှရှိသည်ကို သတ်မှတ်ပေးသည်။

သို့ရာတွင်၊ အစုအဝေးမည်မျှအကောင်းဆုံးဖြစ်မည်ကို ကျွန်ုပ်တို့ကြိုတင်မသိရသောကြောင့် မော်ဒယ်၏ SSE (နှစ်ထပ်ကိန်းအမှားများ) ကိုပြသသည့် ဂရပ်တစ်ခုဖန်တီးရန် လိုအပ်ပါသည်။

ပုံမှန်အားဖြင့်၊ ကျွန်ုပ်တို့သည် ဤဇာတ်ကွက်အမျိုးအစားကို ဖန်တီးသောအခါ၊ စတုရန်းများပေါင်းလဒ်သည် “ကွေးသည်” သို့မဟုတ် အဆင့်မှစတင်သွားသည့် “ ဒူး” ကို ရှာသည်။ ၎င်းသည် ယေဘုယျအားဖြင့် အကောင်းဆုံးအစုအဝေးများဖြစ်သည်။

အောက်ဖော်ပြပါ ကုဒ်သည် x-axis နှင့် y-axis ပေါ်ရှိ အစုအစည်းများ၏ အရေအတွက်ကို ပြသသည့် ဤကွက်အမျိုးအစားကို ဖန်တီးနည်းကို ပြသသည်-

 #initialize kmeans parameters
kmeans_kwargs = {
" init ": " random ",
" n_init ": 10,
" random_state ": 1,
}

#create list to hold SSE values for each k
sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, ** kmeans_kwargs)
    kmeans. fit (scaled_df)
    sse. append (kmeans.inertia_)

#visualize results
plt. plot (range(1, 11), sse)
plt. xticks (range(1, 11))
plt. xlabel (" Number of Clusters ")
plt. ylabel (“ SSE ”)
plt. show () 

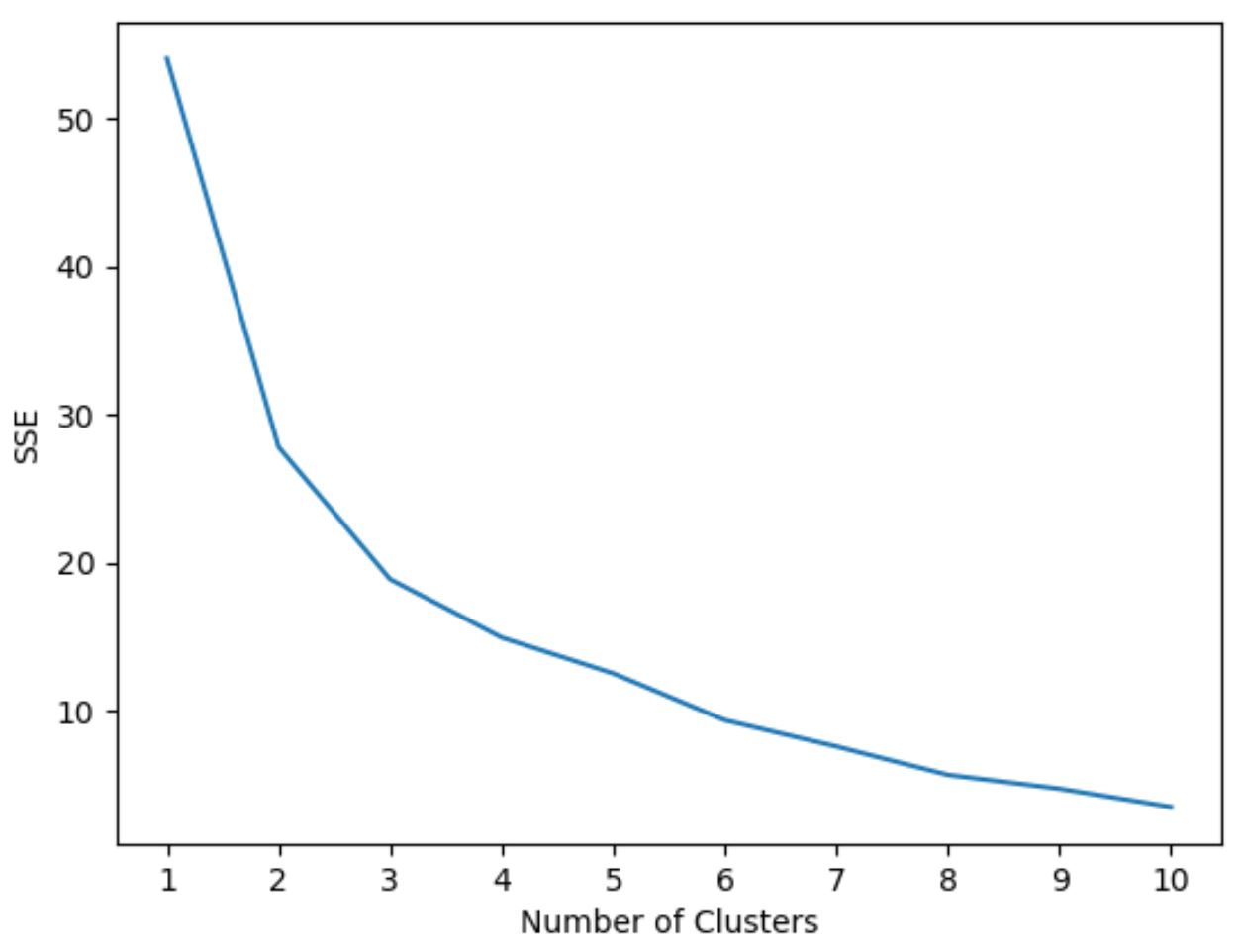
ဤဂရပ်တွင်၊ k = 3 ပြွတ် များတွင် အကွေးအကောက် သို့မဟုတ် “ ဒူး” ရှိနေသည်ကို တွေ့ရပါသည်။

ထို့ကြောင့်၊ နောက်တဆင့်တွင် ကျွန်ုပ်တို့၏ k-Means အစုလိုက်ပုံစံကို ကိုက်ညီသောအခါတွင် အစုအဖွဲ့ 3 ခုကို အသုံးပြုပါမည်။

မှတ်ချက် – လက်တွေ့ကမ္ဘာတွင်၊ အသုံးပြုရန် အစုအဝေးအရေအတွက်ကို ရွေးချယ်ရန် ဤကြံစည်မှုနှင့် ဒိုမိန်းကျွမ်းကျင်မှုပေါင်းစပ်မှုကို အသုံးပြုရန် အကြံပြုထားသည်။

အဆင့် 5- Optimal K ဖြင့် K-Means အစုအဝေးကို လုပ်ဆောင်ပါ။

အောက်ပါကုဒ်သည် k -3 အတွက် အကောင်းဆုံးတန်ဖိုးကို အသုံးပြု၍ ဒေတာအတွဲပေါ်တွင် k-ဆိုလိုရင်း အစုအဝေးကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-

 #instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )

#fit k-means algorithm to data
kmeans. fit (scaled_df)

#view cluster assignments for each observation
kmeans. labels_

array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0]) 

ရလဒ်ဇယားသည် DataFrame ရှိ ကြည့်ရှုမှုတစ်ခုစီအတွက် အစုလိုက်တာဝန်များကို ပြသသည်။

ဤရလဒ်များကို အဓိပ္ပာယ်ဖွင့်ဆိုရန် ပိုမိုလွယ်ကူစေရန်၊ ကစားသမားတစ်ဦးစီ၏ အစုအဝေးတာဝန်ကို ပြသသည့် DataFrame တွင် ကော်လံတစ်ခုကို ထည့်နိုင်သည်-

 #append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_

#view updated DataFrame
print (df)

points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0

အစုအဝေး ကော်လံတွင် ကစားသမားတစ်ဦးစီမှ သတ်မှတ်ထားသော အစုနံပါတ် (0၊ 1 သို့မဟုတ် 2) ပါရှိသည်။

တူညီသော အစုအဝေးမှ ပိုင်ဆိုင်သည့် ကစားသမားများသည် အမှတ်များ ၊ ကူညီပေးခြင်း နှင့် ပြန်လှန်ခြင်း ကော်လံများအတွက် ခန့်မှန်းခြေတူညီသော တန်ဖိုးများရှိသည်။

မှတ်ချက် – sklearn ၏ KMeans လုပ်ဆောင်ချက်အတွက် စာရွက်စာတမ်းအပြည့်အစုံကို ဤနေရာတွင် ရှာနိုင်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ပါ သင်ခန်းစာများသည် Python တွင် အခြားသော အသုံးများသော အလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

Python တွင် linear regression လုပ်နည်း
Python တွင် Logistic Regression ကို မည်သို့လုပ်ဆောင်မည်နည်း။
Python တွင် K-Fold အပြန်အလှန် validation လုပ်ဆောင်နည်း