Stata ရှိ kruskal-wallis စမ်းသပ်မှုပြုလုပ်နည်း

Kruskal-Wallis စမ်းသပ်မှုအား အမှီ အခိုကင်းသော အုပ်စုသုံးစု သို့မဟုတ် ထို့ထက်ပိုသော အလယ်အလတ်အုပ်စုများကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည်။ ၎င်းကို တစ်လမ်းသွား ANOVA ၏ မျဥ်းရိုးမတူညီသော တူညီသည်ဟု ယူဆသည်။

ဤသင်ခန်းစာသည် Stata ရှိ Kruskal-Wallis စမ်းသပ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

Stata ရှိ Kruskal-Wallis စမ်းသပ်မှုပြုလုပ်နည်း

ဤဥပမာအတွက်၊ ကျွန်ုပ်တို့သည် အမေရိကန်ပြည်ထောင်စုရှိ ပြည်နယ်ငါးဆယ်အတွက် 1980 သန်းခေါင်စာရင်းဒေတာပါရှိသော သန်းခေါင်စာရင်း ဒေတာအတွဲကို အသုံးပြုပါမည်။ ဒေတာအတွဲတွင် ပြည်နယ်များကို မတူညီသောဒေသ လေးခုအဖြစ် အမျိုးအစားခွဲခြားထားသည်။

• Nord Est
• မြောက် အလယ်ပိုင်း
• တောင်
• အနောက်

ဤဒေသလေးခုတွင် ပျမ်းမျှအသက်သည် တန်းတူဖြစ်မဖြစ် ဆုံးဖြတ်ရန် Kruskal-Wallis စမ်းသပ်မှုကို လုပ်ဆောင်ပါမည်။

အဆင့် 1: ဒေတာကိုတင်ပြီးပြသပါ။

ပထမဦးစွာ၊ Command box တွင်အောက်ပါ command ကိုရိုက်ခြင်းဖြင့် dataset ကိုတင်ပါ-

https://www.stata-press.com/data/r13/census ကို အသုံးပြုပါ။

အောက်ပါ command ကို အသုံးပြု၍ ဒေတာအတွဲ၏ အမြန်အနှစ်ချုပ်ကို ရယူပါ-

အကျဉ်းချုပ်ရန်

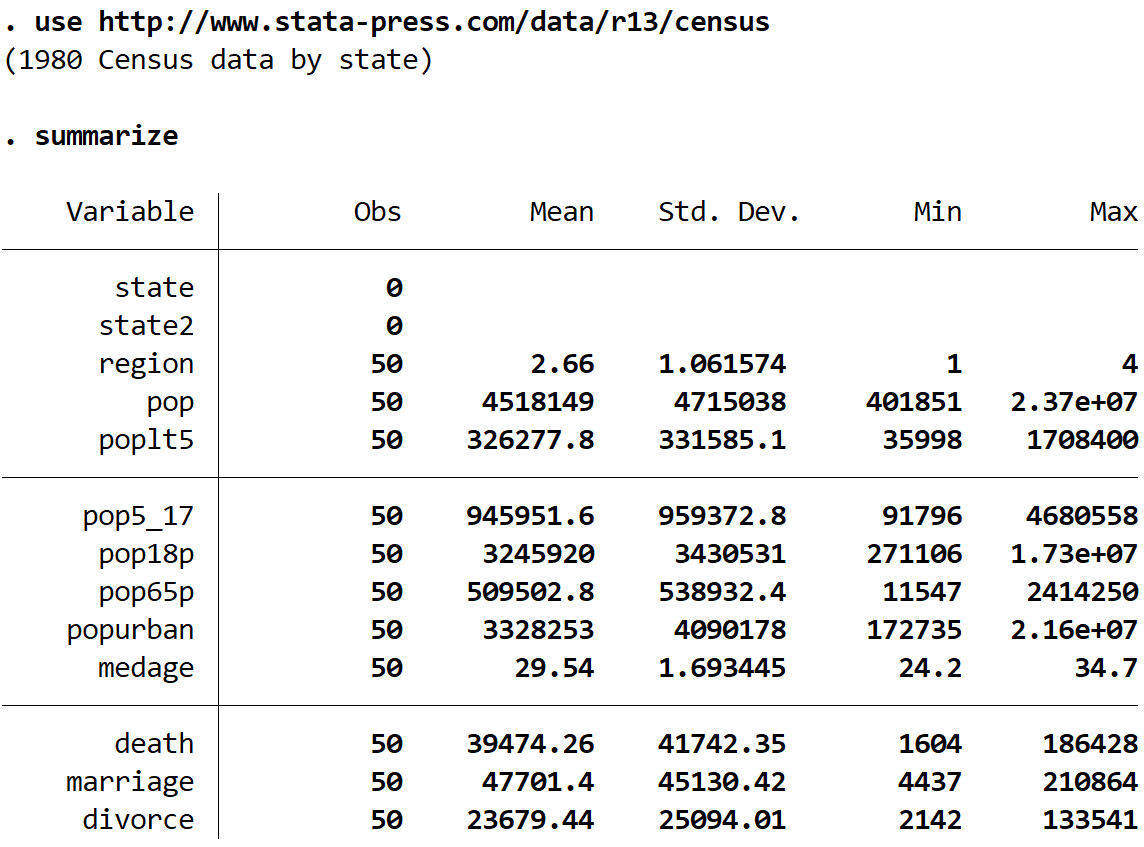
ဤဒေတာအတွဲတွင် မတူညီသော ကိန်းရှင် 13 ခုရှိကြောင်း ကျွန်ုပ်တို့တွေ့မြင်နိုင်သော်လည်း ကျွန်ုပ်တို့နှင့်အတူ လုပ်ဆောင်မည့် နှစ်ခုမှာ medage (ပျမ်းမျှအသက်) နှင့် ဒေသ ဖြစ်သည်။

အဆင့် 2- ဒေတာကို မြင်ယောင်ကြည့်ပါ။

Kruskal-Wallis စမ်းသပ်မှုကို မလုပ်ဆောင်မီ၊ ဒေသလေးခုတစ်ခုစီအတွက် ပျမ်းမျှအသက်ဖြန့်ဖြူးမှုကို မြင်သာစေရန် အကွက်ကွက် အချို့ကို ဦးစွာဖန်တီးကြပါစို့။

medage graphic box၊ on (ဒေသ)

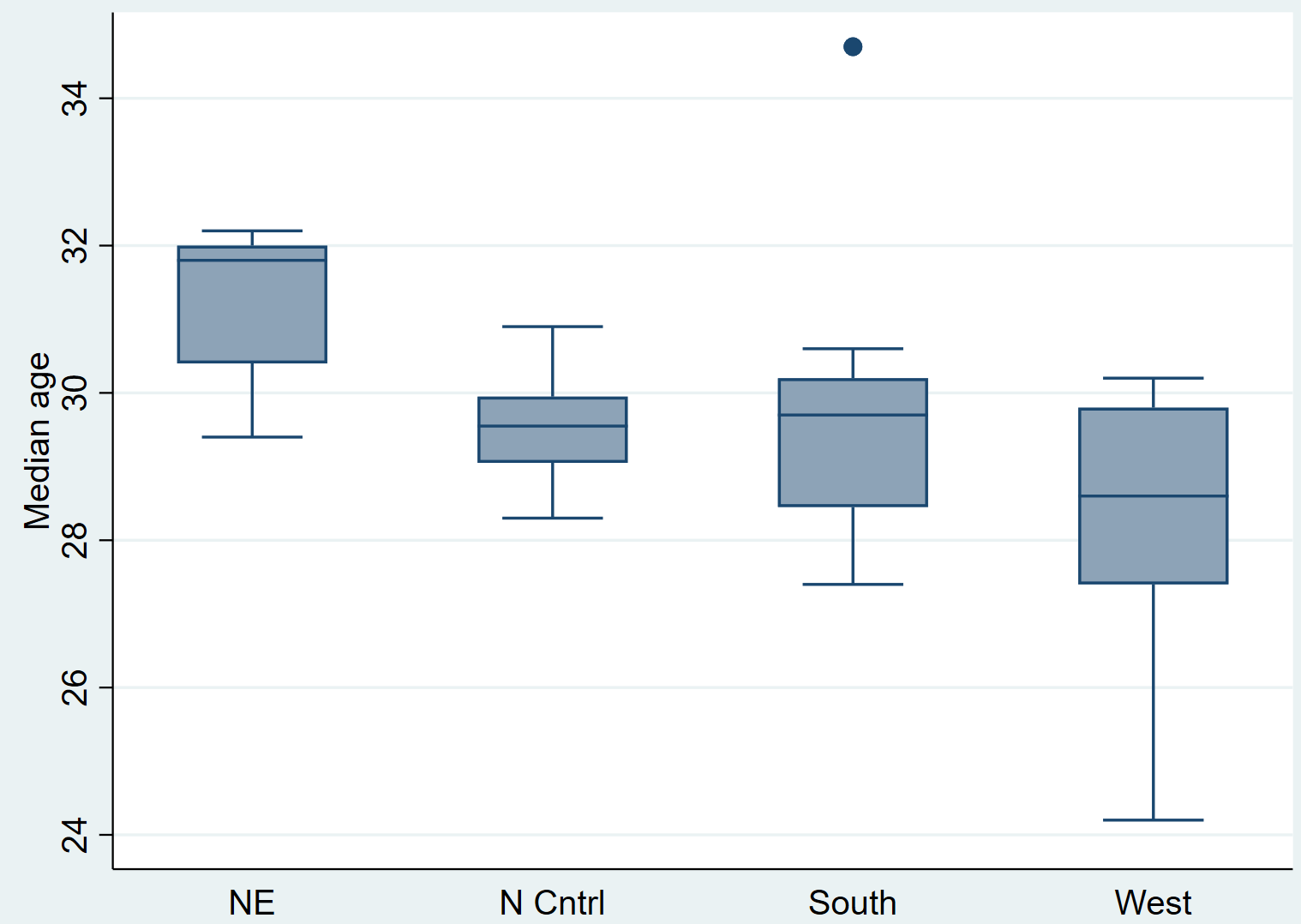
အကွက်ကွက်များကို ကြည့်ရုံဖြင့် ဖြန့်ဖြူးမှုများသည် ဒေသတစ်ခုနှင့်တစ်ခု ကွဲပြားနေပုံပေါ်သည်။ ထို့နောက် ဤကွာခြားချက်များသည် စာရင်းအင်းအရ သိသာထင်ရှားမှုရှိမရှိ သိရန် Kruskal-Wallis စမ်းသပ်မှုကို လုပ်ဆောင်ပါမည်။

အဆင့် 3- Kruskal-Wallis စမ်းသပ်မှုပြုလုပ်ပါ။

Kruskal-Wallis စမ်းသပ်မှုကို လုပ်ဆောင်ရန် အောက်ပါ syntax ကို အသုံးပြုပါ ။

kwallis measure_variable၊ (grouping_variable အားဖြင့်)

ကျွန်ုပ်တို့၏အခြေအနေတွင်၊ ကျွန်ုပ်တို့သည် အောက်ပါ syntax ကိုအသုံးပြုပါမည်။

kwallis medage၊ (ဒေသအလိုက်)

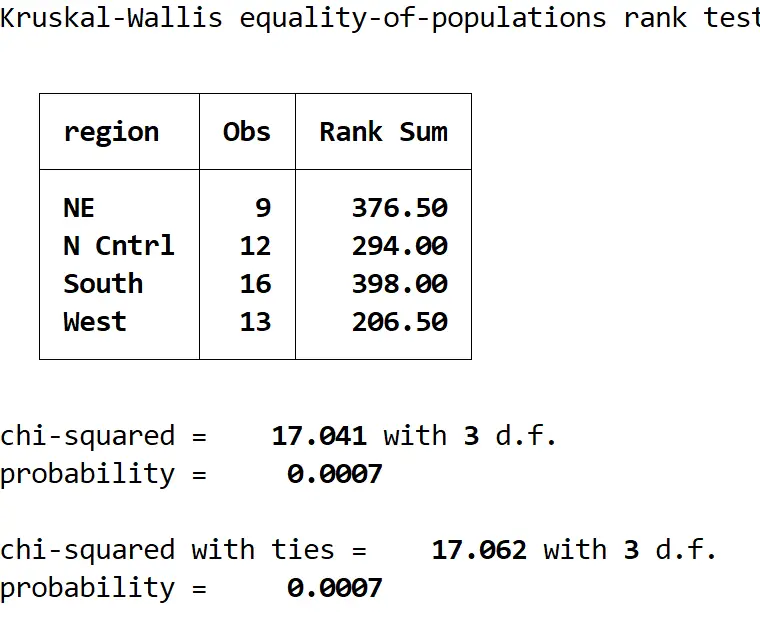
ဤသည်မှာ ရလဒ်ကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-

အနှစ်ချုပ်ဇယား- ဤဇယားသည် ဒေသတစ်ခုစီမှ စောင့်ကြည့်မှုအရေအတွက်နှင့် ဒေသတစ်ခုစီအတွက် အဆင့်သတ်မှတ်ချက်များကို ပြသသည်။

Chi-square နှင့် ဆက်စပ်မှု- ဤသည်မှာ 17.062 ဖြစ်သည့် စမ်းသပ်ကိန်းဂဏန်း၏တန်ဖိုးဖြစ်သည်။

ဖြစ်နိုင်ခြေ- ဤသည်မှာ 0.0007 ဖြစ်သည့် စမ်းသပ်စာရင်းအင်းနှင့် ကိုက်ညီသော p-တန်ဖိုးဖြစ်သည်။ ဤတန်ဖိုးသည် 0.05 ထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့သည် null hypothesis ကိုငြင်းပယ်နိုင်ပြီး အလယ်တန်းအသက်သည် နယ်ပယ်လေးခုတွင် မညီမျှကြောင်း ကောက်ချက်ချနိုင်ပါသည်။

အဆင့် 4- ရလဒ်များကို သတင်းပို့ပါ။

နောက်ဆုံးအနေနဲ့၊ Kruskal-Wallis စမ်းသပ်မှုရလဒ်တွေကို အစီရင်ခံချင်ပါတယ်။ ဤသည်မှာ မည်သို့လုပ်ဆောင်ရမည်ကို ဥပမာတစ်ခုဖြစ်သည်။

အမေရိကန်ပြည်ထောင်စု၏ အောက်ပါဒေသလေးခုတွင် လူတစ်ဦးချင်းစီ၏ ပျမ်းမျှအသက်သည် တူညီခြင်းရှိမရှိ ဆုံးဖြတ်ရန် Kruskal-Wallist စမ်းသပ်မှုကို ပြုလုပ်ခဲ့သည်-

• အရှေ့မြောက် (n=9)
• အလယ်ပိုင်း (n=12)၊
• တောင် (n=16)
• အနောက် (n=13)

စမ်းသပ်မှုတွင် ဒေသလေးခုတွင် လူတစ်ဦးချင်းစီ၏ ပျမ်းမျှအသက် (X ² = 17.062၊ p = 0.0007) တူညီမည်မဟုတ်ကြောင်း စမ်းသပ်တွေ့ရှိခဲ့သည်။ ဆိုလိုသည်မှာ၊ ဒေသနှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော ဒေသနှစ်ခုကြားရှိ ပျမ်းမျှအသက်အရွယ်တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ကွာခြားချက်ရှိခဲ့သည်။