Ti-84 ဂဏန်းတွက်စက်ပေါ်တွင် linear regression လုပ်ဆောင်နည်း

Linear regression သည် ရှင်းပြထားသော variable၊ x နှင့် response variable, y တို့ကြား ဆက်နွယ်မှုကို နားလည်ရန် ကျွန်ုပ်တို့ အသုံးပြုနိုင်သော နည်းလမ်းတစ်ခုဖြစ်သည်။

ဤသင်ခန်းစာသည် TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် linear regression လုပ်နည်းကို ရှင်းပြထားသည်။

ဥပမာ- TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် မျဉ်းကြောင်းပြန်ဆုတ်ခြင်း။

စာမေးပွဲအတွက် ကျောင်းသားတစ်ဦး၏ သင်ကြားမှု နာရီအရေအတွက်နှင့် စာမေးပွဲတွင် ၎င်းတို့ရရှိသည့် အတန်းကြား ဆက်နွယ်မှုကို ကျွန်ုပ်တို့ နားလည်လိုသည်ဆိုပါစို့။

ဤဆက်နွယ်မှုကို စူးစမ်းလေ့လာရန်၊ တုံ့ပြန်မှုကိန်းရှင်အဖြစ် လေ့လာထားသော နာရီများကို အသုံးပြု၍ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုလုပ်ဆောင်ရန် TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် အောက်ပါအဆင့်များကို လုပ်ဆောင်နိုင်ပါသည်။

အဆင့် 1: ဒေတာကိုထည့်ပါ။

ပထမဦးစွာ၊ ကျွန်ုပ်တို့သည် explanatory variable နှင့် response variable အတွက် ဒေတာတန်ဖိုးများကို ထည့်သွင်းပါမည်။ Stat ကိုနှိပ်ပြီး EDIT ကို နှိပ်ပါ။ ကော်လံ L1 တွင် ဖော်ပြထားသော ကိန်းရှင် (လေ့လာထားသော နာရီ) အတွက် အောက်ပါတန်ဖိုးများနှင့် ကော်လံ L2 ရှိ တုံ့ပြန်မှုကိန်းရှင် (စာမေးပွဲရမှတ်) အတွက် တန်ဖိုးများကို ထည့်သွင်းပါ-

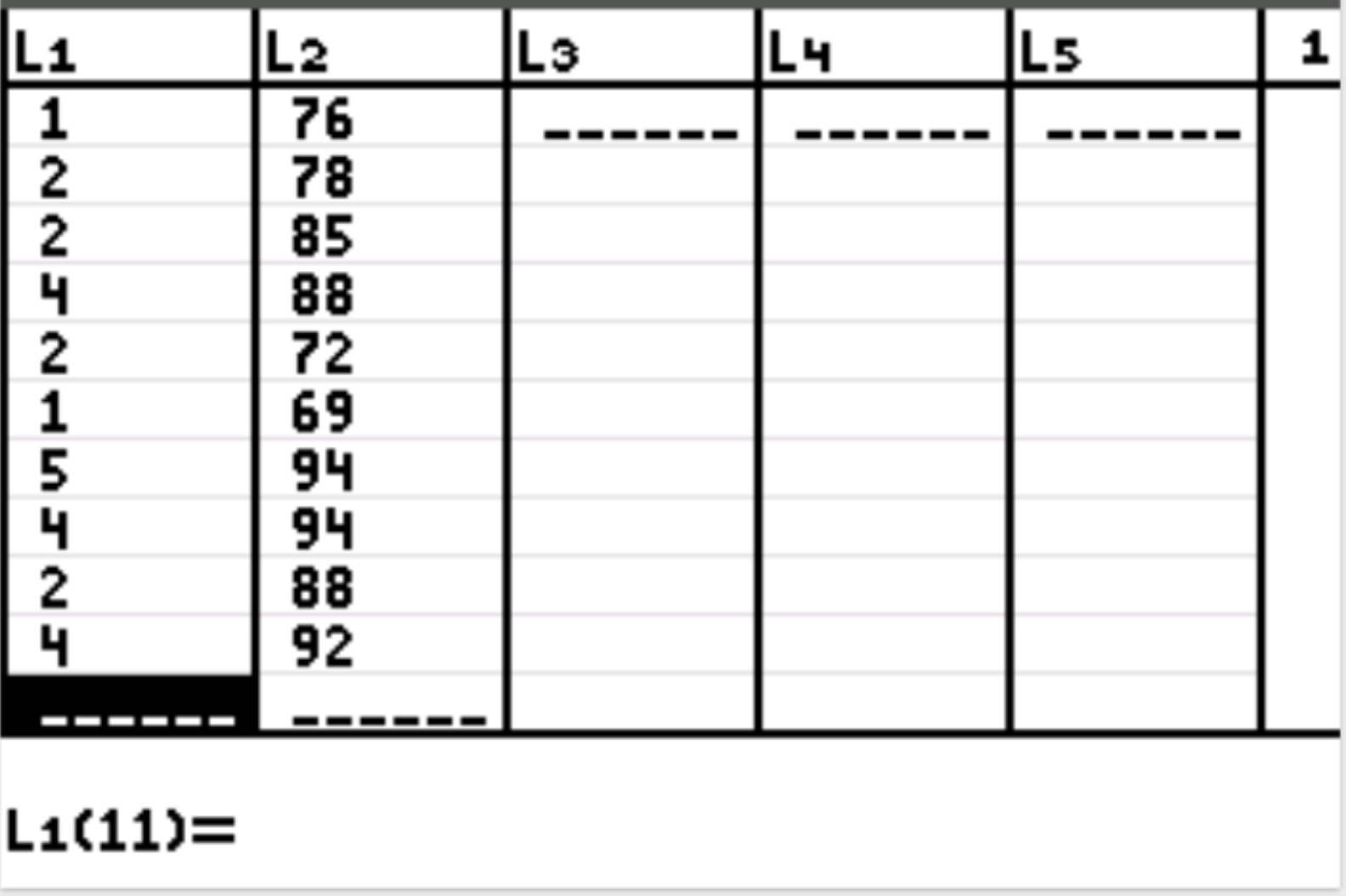
အဆင့် 2- linear regression လုပ်ဆောင်ပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် linear regression ကိုလုပ်ဆောင်ပါမည်။ Stat ကိုနှိပ်ပြီး CALC သို့ ရွှေ့ပါ။ ထို့နောက် 8- Linreg(a+bx) သို့ ရွှေ့ပြီး Enter နှိပ်ပါ။

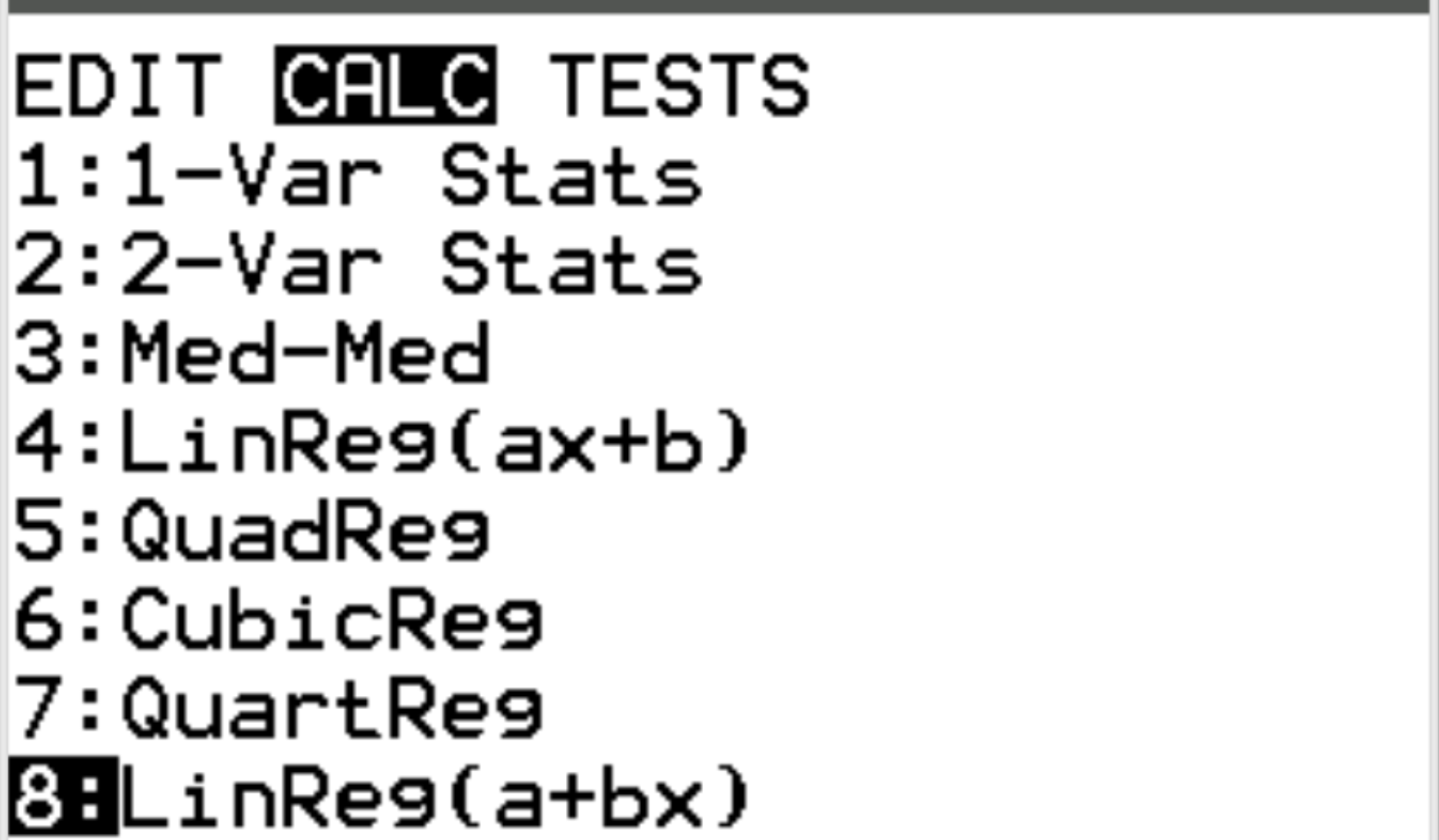
Xlist နှင့် Ylist အတွက်၊ ဤအရာများသည် ကျွန်ုပ်တို့၏ဒေတာထည့်သွင်းရန်အသုံးပြုသည့်ကော်လံများဖြစ်သောကြောင့် L1 နှင့် L2 ကို ရွေးချယ်ထားကြောင်း သေချာပါစေ။ FreqList ကို ကွက်လပ်ထားလိုက်ပါ။ တွက်ချက်ရန် အောက်သို့ဆင်းပြီး Enter နှိပ်ပါ။ အောက်ပါ output သည် အလိုအလျောက် ပေါ်လာလိမ့်မည်-

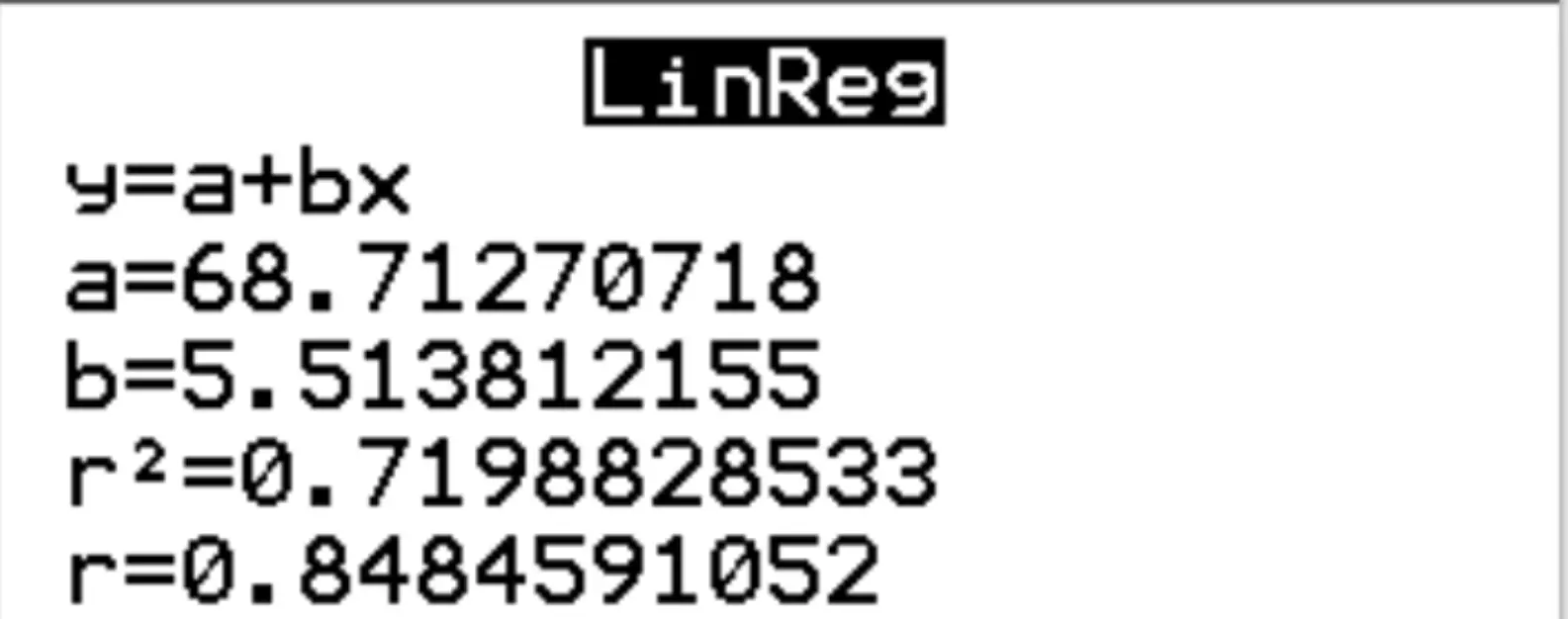
အဆင့် 3- ရလဒ်များကို ဘာသာပြန်ပါ။

ရလဒ်များမှ၊ ခန့်မှန်းခြေဆုတ်ယုတ်မှုညီမျှခြင်းမှာ-

စာမေးပွဲရမှတ် = 68.7127 + 5.5138*(နာရီ)

ထပ်လောင်းလေ့လာထားသော နာရီတိုင်းအတွက် ပျမ်းမျှအားဖြင့် စာမေးပွဲရမှတ်သည် 5.5138 တိုးသင့်သည်ဟု ဆိုလိုရန် နာရီများ၏ ကိန်းကို ဘာသာပြန်ဆိုပါသည်။ သုညနာရီလေ့လာနေသော ကျောင်းသားအတွက် မျှော်မှန်းထားသော စာမေးပွဲရမှတ်သည် 68.7127 ဖြစ်သည်ဟု ဆိုလိုရန် ကြားဖြတ်၏ ကိန်းကို ဘာသာပြန်ဆိုပါသည်။

လေ့လာမှုနာရီအရေအတွက်ပေါ်မူတည်၍ ကျောင်းသားတစ်ဦးအတွက် မျှော်မှန်းထားသော စာမေးပွဲရမှတ်ကို တွက်ချက်ရန် ဤခန့်မှန်းခြေဆုတ်ခြင်းညီမျှခြင်းကို ကျွန်ုပ်တို့အသုံးပြုနိုင်ပါသည်။

ဥပမာအားဖြင့်၊ သုံးနာရီကြာလေ့လာသော ကျောင်းသားသည် စာမေးပွဲရမှတ် 85.25 ရရှိသင့်သည် ။

စာမေးပွဲရမှတ် = 68.7127 + 5.5138*(3) = 85.25

ဆုတ်ယုတ်မှုပုံစံအတွက် r နှစ်ထပ်ကိန်းသည် r ² = 0.7199 ဟုလည်း မြင်နိုင်သည်။

ဤတန်ဖိုးကို ကိန်းဂဏန်းသတ်မှတ်ခြင်းဟု ခေါ်သည်။ ၎င်းသည် explanatory variable ဖြင့် ရှင်းပြနိုင်သော တုံ့ပြန်မှု variable ရှိ ကွဲလွဲမှု၏ အချိုးအစားဖြစ်သည်။ ဤဥပမာတွင်၊ စာမေးပွဲရမှတ်များ ကွဲလွဲမှု၏ 71.99% ကို လေ့လာသည့် နာရီအရေအတွက်ဖြင့် ရှင်းပြနိုင်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် ကျန်ရှိသော ဇာတ်ကွက်တစ်ခုကို ဖန်တီးနည်း
TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် Quadratic Regression လုပ်ဆောင်နည်း
TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် အညွှန်းကိန်း ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်နိုင်မည်နည်း။