Google sheets တွင် linear regression လုပ်နည်း

Linear regression သည် တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ရှင်းပြထားသော variable များ နှင့် တုံ့ပြန်မှု variable အကြား ဆက်နွယ်မှုကို အရေအတွက်သတ်မှတ်ရန် အသုံးပြုနိုင်သော နည်းလမ်းတစ်ခုဖြစ်သည်။

ရှင်းပြနိုင်သောကိန်းရှင်တစ်ခုသာရှိပြီး ကွဲပြားသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုနှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသောရှင်းပြချက်တစ်ခုရှိသောအခါ ကျွန်ုပ်တို့သည် ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုကိုအသုံးပြုသည်။

အောက်ဖော်ပြပါ syntax ကိုအသုံးပြုသည့် Google Sheets LINEST() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ ဆုတ်ယုတ်မှု အမျိုးအစားနှစ်မျိုးလုံးကို လုပ်ဆောင်နိုင်သည်-

LINEST (လူသိများ_data_y၊ သိပြီး_data_x၊ တွက်ချက်_b၊ စကားအသုံးအနှုန်း)

ရွှေ-

• know_data_y- တုံ့ပြန်မှုတန်ဖိုးများ ခင်းကျင်းမှု
• Know_data_x- ရှင်းလင်းချက်တန်ဖိုးများ ဇယား
• calculate_b: ကြားဖြတ်ကို တွက်ချက်ခြင်း ရှိ၊ မရှိ ညွှန်ပြသည်။ ၎င်းသည် ပုံသေအားဖြင့် မှန်ကန်ပြီး မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းအတွက် ၎င်းကို ကျွန်ုပ်တို့ချန်ထားခဲ့သည်။
• စကားအသုံးအနှုန်း- ကုန်းစောင်းနှင့် ကြားဖြတ်ရုံထက် ကျော်လွန်သည့် နောက်ဆက်တွဲ ဆုတ်ယုတ်မှုစာရင်းအင်းများကို ပံ့ပိုးပေးနိုင်ခြင်း ရှိ၊မရှိ ညွှန်ပြသည်။ ၎င်းသည် ပုံသေအားဖြင့် မှားနေသည်၊ သို့သော် ကျွန်ုပ်တို့၏နမူနာများတွင် ၎င်းသည် မှန်ကန်ကြောင်း ကျွန်ုပ်တို့ သတ်မှတ်ပါမည်။

အောက်ဖော်ပြပါ ဥပမာများသည် ဤလုပ်ဆောင်ချက်ကို လက်တွေ့အသုံးချနည်းကို ပြသထားသည်။

Google Sheets တွင် ရိုးရှင်းသော မျဉ်းကြောင်းပြန်ဆုတ်ခြင်း။

လေ့လာသည့်နာရီ နှင့် စာမေးပွဲရလဒ်ကြား ဆက်စပ်မှုကို နားလည်လိုသည်ဆိုပါစို့။ စာမေးပွဲနှင့် စာမေးပွဲတွင် ရရှိသော အတန်းတို့ကို လေ့လာသည်။

ဤဆက်နွယ်မှုကို စူးစမ်းလေ့လာရန်၊ တုံ့ပြန်မှု ကိန်းရှင်အဖြစ် လေ့လာထားသော နာရီများကို အသုံးပြု၍ ရိုးရှင်းသော မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းကို လုပ်ဆောင်နိုင်ပါသည်။

အောက်ဖော်ပြပါ ဖန်သားပြင်ဓာတ်ပုံသည် ဆဲလ် D2 တွင် အသုံးပြုသည့် အောက်ဖော်ပြပါ ပုံသေနည်းပါ ကျောင်းသား 20 ဦး၏ ဒေတာအတွဲကို အသုံးပြု၍ ရိုးရှင်းသော မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-

= LINE ( B2:B21 ၊ A2:A21 ၊ TRUE ၊ TRUE )

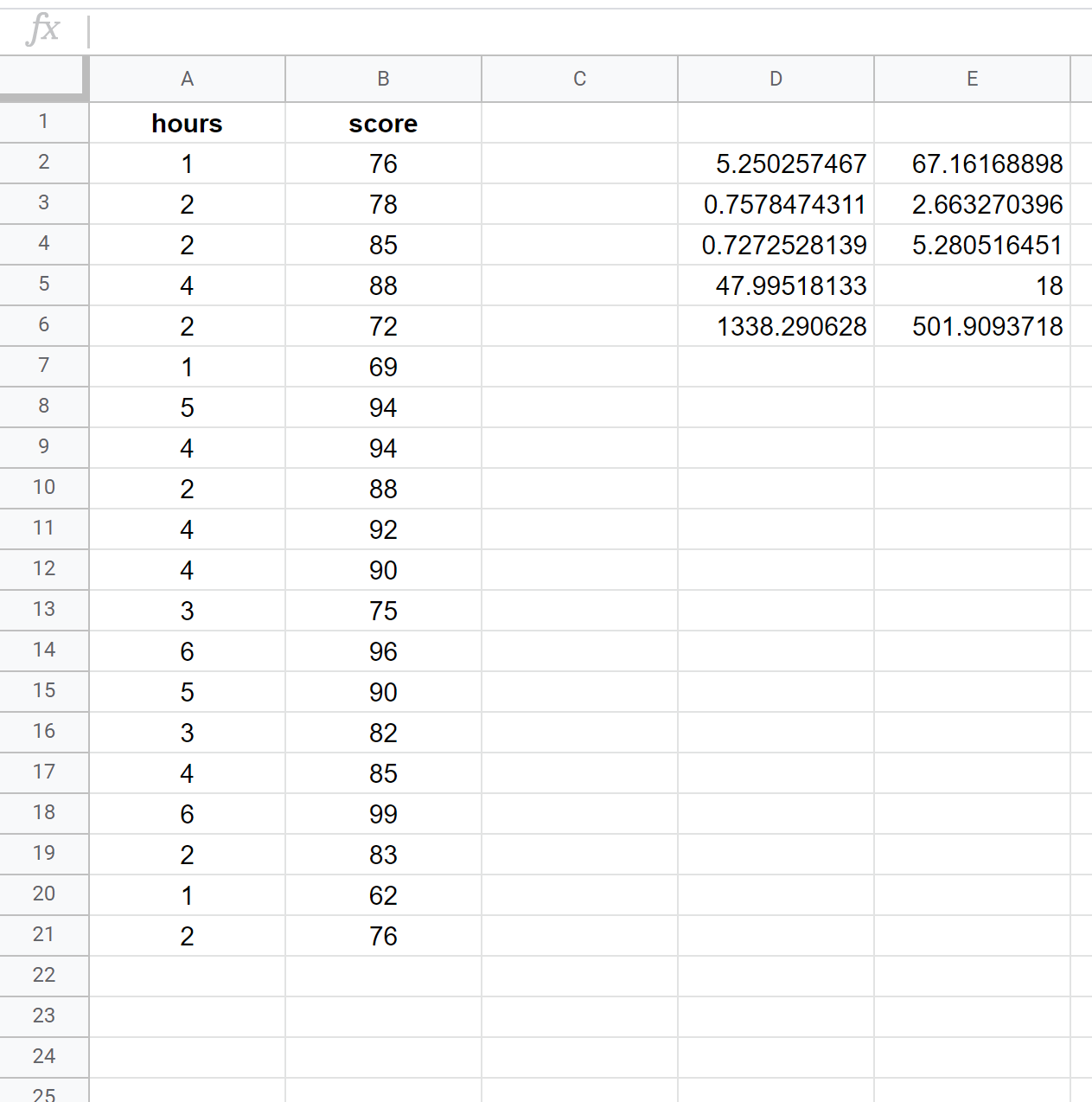
အောက်ပါ ဖန်သားပြင်ဓာတ်ပုံသည် အထွက်အတွက် မှတ်ချက်များကို ပေးသည်-

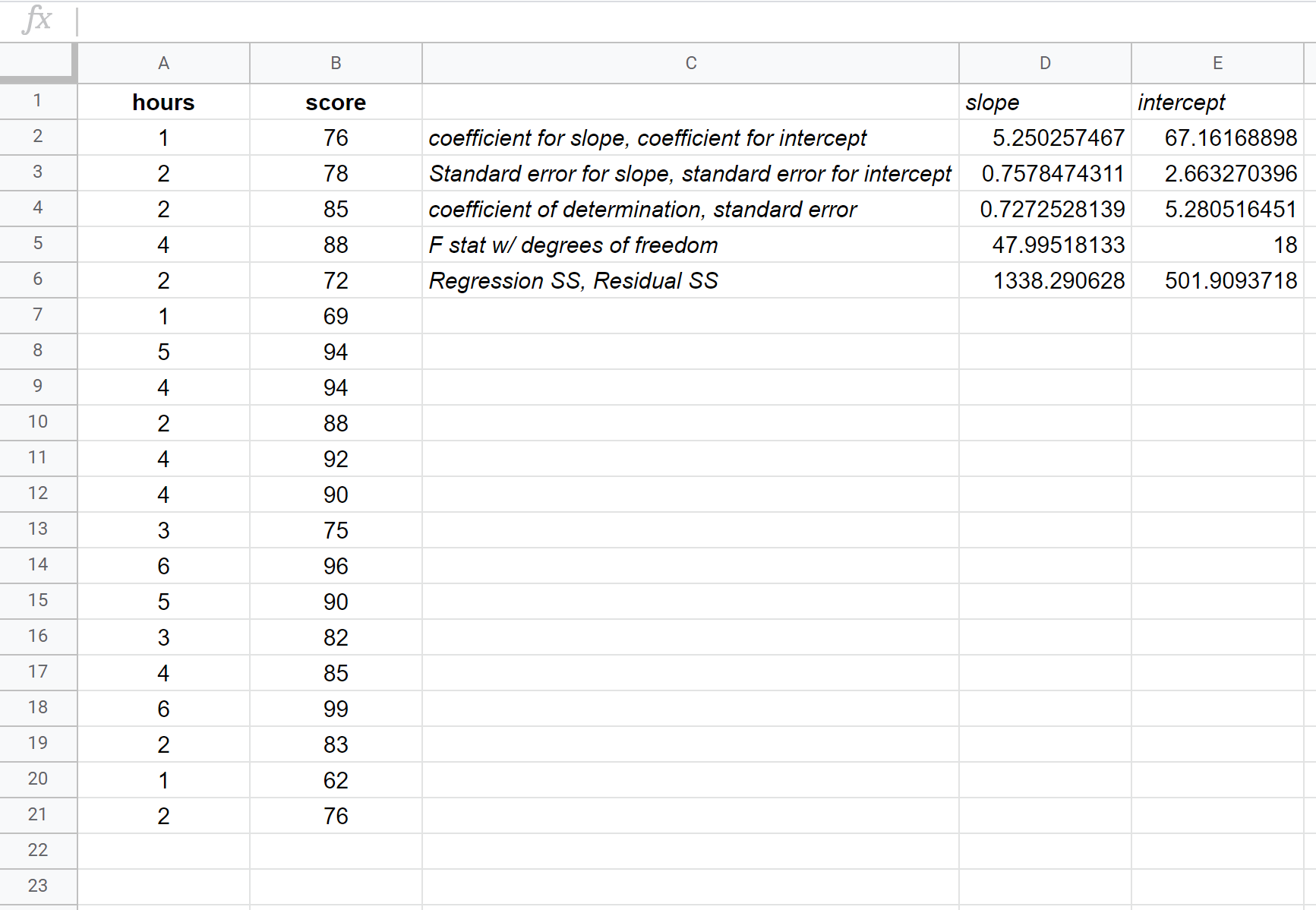
ရလဒ်တွင် အသက်ဆိုင်ဆုံး ဂဏန်းများကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုရမည်ကို ဤတွင် ဖော်ပြပါရှိသည်။

R စတုရန်း- 0.72725 ။ ဒါကို coefficient of determination လို့ခေါ်တယ်။ ၎င်းသည် explanatory variable ဖြင့် ရှင်းပြနိုင်သော တုံ့ပြန်မှု variable ရှိ ကွဲလွဲမှု၏ အချိုးအစားဖြစ်သည်။ ဤဥပမာတွင်၊ စာမေးပွဲရမှတ်များတွင် ကွဲလွဲမှု ခန့်မှန်းခြေ 72.73% ကို လေ့လာသည့် နာရီအရေအတွက်ဖြင့် ရှင်းပြနိုင်သည်။

စံအမှား- 5.2805 ။ ၎င်းသည် သတိပြုမိသောတန်ဖိုးများနှင့် ဆုတ်ယုတ်မှုမျဉ်းကြားရှိ ပျမ်းမျှအကွာအဝေးဖြစ်သည်။ ဤဥပမာတွင်၊ လေ့လာထားသောတန်ဖိုးများသည် ဆုတ်ယုတ်မှုမျဉ်းမှ ပျမ်းမျှယူနစ် 5.2805 ဖြင့် သွေဖည်သွားပါသည်။

Coefficients- ကိန်းဂဏန်းများသည် ခန့်မှန်းခြေဆုတ်ယုတ်မှုညီမျှခြင်းကိုရေးရန် လိုအပ်သောနံပါတ်များကိုပေးသည်။ ဤဥပမာတွင်၊ ခန့်မှန်းခြေဆုတ်ယုတ်မှုညီမျှခြင်းမှာ-

စာမေးပွဲရမှတ် = 67.16 + 5.2503*(နာရီ)

ထပ်လောင်းလေ့လာထားသောနာရီတိုင်းအတွက်၊ ပျမ်းမျှအားဖြင့် စာမေးပွဲရမှတ်သည် 5.2503 တိုးသင့်သည်ဟု ဆိုလိုရန် နာရီများ၏ coefficient ကို ဘာသာပြန်ဆိုပါသည်။ သုညနာရီလေ့လာနေသော ကျောင်းသားအတွက် မျှော်မှန်းထားသော စာမေးပွဲရမှတ်သည် 67.16 ဖြစ်သည်ဟု ဆိုလိုရန် ကြားဖြတ်၏ ကိန်းကို ဘာသာပြန်ဆိုပါသည်။

လေ့လာမှုနာရီအရေအတွက်ပေါ်မူတည်၍ ကျောင်းသားတစ်ဦးအတွက် မျှော်မှန်းထားသော စာမေးပွဲရမှတ်ကို တွက်ချက်ရန် ဤခန့်မှန်းခြေဆုတ်ခြင်းညီမျှခြင်းကို ကျွန်ုပ်တို့အသုံးပြုနိုင်ပါသည်။ ဥပမာအားဖြင့်၊ သုံးနာရီကြာလေ့လာသော ကျောင်းသားသည် စာမေးပွဲရမှတ် 82.91 ရရှိသင့်သည်-

စာမေးပွဲရမှတ် = 67.16 + 5.2503*(3) = 82.91

Google Sheets တွင် Linear Regression များစွာ

ကျောင်းတက်ခဲ့ရတဲ့ နာရီအရေအတွက်နဲ့ ကြိုတင်ပြင်ဆင်တဲ့ စာမေးပွဲအရေအတွက်က ကောလိပ်ဝင်ခွင့်စာမေးပွဲမှာ ကျောင်းသားတစ်ယောက်ရဲ့ အတန်းကို သက်ရောက်မှုရှိမရှိ သိချင်တယ်ဆိုပါစို့။

ဤဆက်နွယ်မှုကို စူးစမ်းလေ့လာရန်၊ ကျွန်ုပ်တို့သည် တုံ့ပြန်မှုကိန်းရှင်များအဖြစ် ဖြေဆိုထားသော ကိန်းရှင်များနှင့် စာမေးပွဲရလဒ်များ အဖြစ် ပြုလုပ်ထားသော နာရီများ နှင့် ကြိုတင်ပြင်ဆင်မှုစာမေးပွဲများကို အသုံးပြု၍ မျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှုများစွာကို လုပ်ဆောင်နိုင်ပါသည်။

အောက်ဖော်ပြပါ ဖန်သားပြင်ဓာတ်ပုံသည် ဆဲလ် E2 တွင် အသုံးပြုသည့် အောက်ဖော်ပြပါဖော်မြူလာဖြင့် ကျောင်းသား 20 ဦး၏ ဒေတာအတွဲကို အသုံးပြု၍ မျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှုများစွာကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-

= RIGHT ( C2:C21 ၊ A2:B21 ၊ TRUE ၊ TRUE )

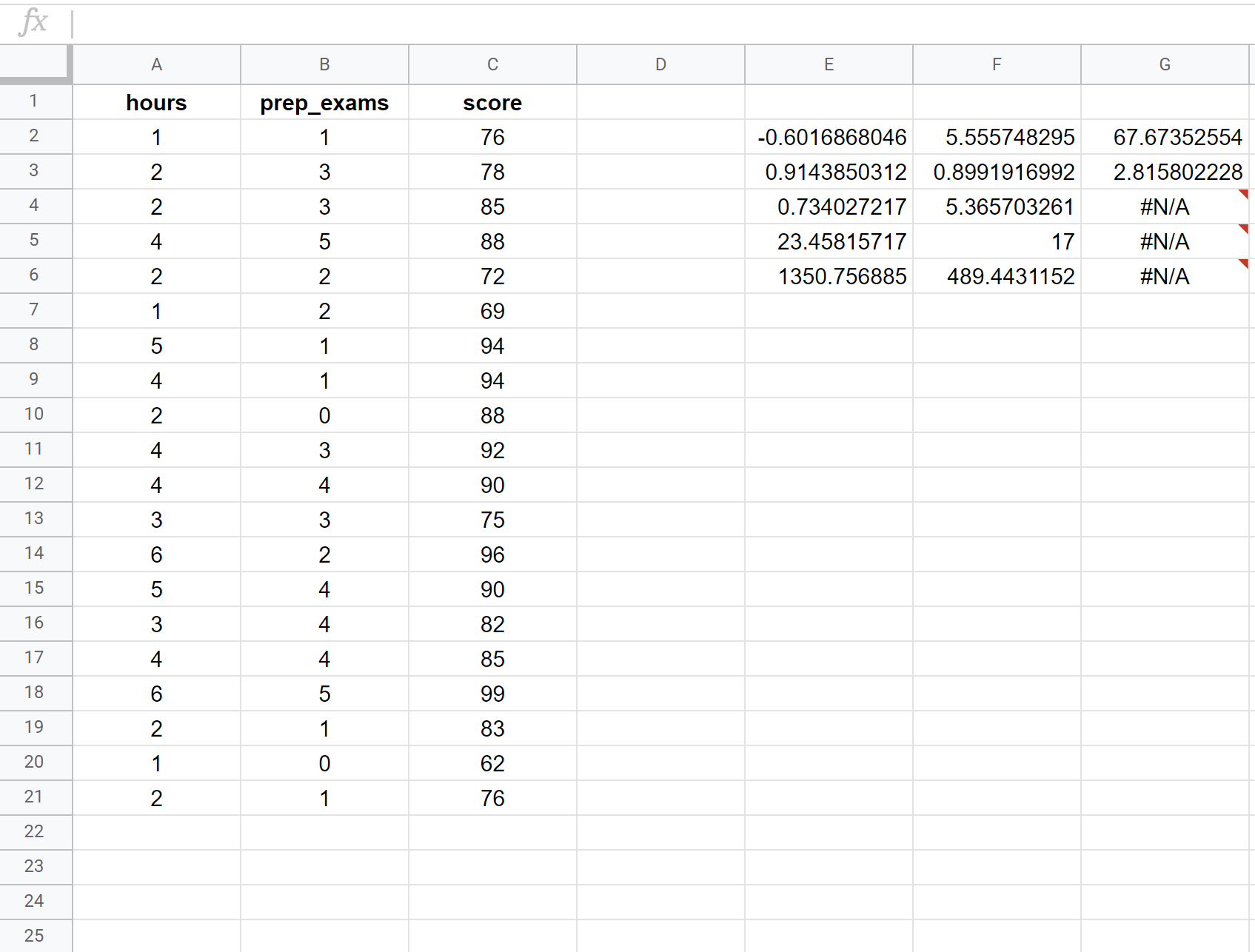
ရလဒ်တွင် အသက်ဆိုင်ဆုံး ဂဏန်းများကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုရမည်ကို ဤတွင် ဖော်ပြပါရှိသည်။

R စတုရန်း- 0.734 ။ ဒါကို coefficient of determination လို့ခေါ်တယ်။ ၎င်းသည် explanatory variable များဖြင့် ရှင်းပြနိုင်သော တုံ့ပြန်မှု variable ၏ ကွဲလွဲမှုအချိုးအစားဖြစ်သည်။ ဤဥပမာတွင်၊ စာမေးပွဲရမှတ်များ ကွဲလွဲမှု၏ 73.4% ကို လေ့လာသည့် နာရီအရေအတွက်နှင့် ကြိုတင်ပြင်ဆင်ထားသော စာမေးပွဲအရေအတွက်ဖြင့် ရှင်းပြထားသည်။

စံအမှား- 5.3657 ။ ၎င်းသည် သတိပြုမိသောတန်ဖိုးများနှင့် ဆုတ်ယုတ်မှုမျဉ်းကြားရှိ ပျမ်းမျှအကွာအဝေးဖြစ်သည်။ ဤဥပမာတွင်၊ လေ့လာထားသောတန်ဖိုးများသည် ဆုတ်ယုတ်မှုမျဉ်းမှ ပျမ်းမျှယူနစ် 5.3657 ဖြင့် သွေဖည်သွားပါသည်။

ခန့်မှန်းခြေဆုတ်ယုတ်မှုညီမျှခြင်း- အောက်ဖော်ပြပါ ခန့်မှန်းခြေဆုတ်ယုတ်မှုညီမျှခြင်းကို ဖန်တီးရန် မော်ဒယ်အထွက်မှ ကိန်းများကို ကျွန်ုပ်တို့အသုံးပြုနိုင်သည်-

စာမေးပွဲရမှတ် = 67.67 + 5.56*(နာရီ) – 0.60*(အကြိုစာမေးပွဲများ)

ကျောင်းသားတစ်ဦးအတွက် မျှော်မှန်းထားသော စာမေးပွဲရမှတ်ကို တွက်ချက်ရန် ဤခန့်မှန်းခြေဆုတ်ခြင်းညီမျှခြင်းကို အသုံးပြု၍ စာသင်ချိန်နာရီအရေအတွက်နှင့် ၎င်းတို့ဖြေဆိုသော အလေ့အကျင့် စာမေးပွဲအရေအတွက်အပေါ် အခြေခံ၍ ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။ ဥပမာအားဖြင့်၊ သုံးနာရီကြာလေ့လာပြီး ကြိုတင်စာမေးပွဲဖြေဆိုသော ကျောင်းသားတစ်ဦးသည် 83.75 အဆင့်ကို ရသင့်သည်-

စာမေးပွဲရမှတ် = 67.67 + 5.56*(3) – 0.60*(1) = 83.75

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် Google Sheets တွင် အခြားသော အသုံးများသည့် အလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

Google Sheets တွင် polynomial regression လုပ်နည်း
Google Sheets တွင် ကျန်ရှိသော Plot တစ်ခုကို ဖန်တီးနည်း