Simple linear regression နိဒါန်း

ရိုးရှင်းသော linear regression သည် variable နှစ်ခုဖြစ်သော x နှင့် y အကြား ဆက်နွယ်မှုကို နားလည်ရန် သင်အသုံးပြုနိုင်သော ကိန်းဂဏန်းဆိုင်ရာ နည်းလမ်းတစ်ခုဖြစ်သည်။

variable, x ကို ခန့်မှန်းသူ variable ဟုခေါ်သည်။

အခြားကိန်းရှင် y ကို တုံ့ပြန်မှု ကိန်းရှင် ဟု ခေါ်သည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် လူခုနစ်ဦး၏ ကိုယ်အလေးချိန်နှင့် အရပ်အမြင့်ပါ အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။

အလေးချိန်ကို ခန့်မှန်းကိန်းကိန်းအဖြစ် သတ်မှတ်ပြီး အမြင့်သည် တုံ့ပြန်မှုကိန်းရှင်ဖြစ်ပါစေ။

အကယ်၍ ကျွန်ုပ်တို့သည် ဤကိန်းရှင်နှစ်ခုကို scatterplot ကိုအသုံးပြု၍ x-axis နှင့် y-axis ပေါ်ရှိ အမြင့်နှင့် အလေးချိန်ဖြင့် ဇယားကွက်ကြည့်မည်ဆိုလျှင်၊ ၎င်းသည် ပုံသဏ္ဌာန်ဖြစ်သည်။

ကိုယ်အလေးချိန် နှင့် အရပ် အကြား ဆက်စပ်မှုကို နားလည်လိုသည် ဆိုပါစို့။ အလေးချိန်တိုးလာသည်နှင့်အမျှ အရပ်လည်းတိုးတတ်သည်ကို ရှင်းရှင်းလင်းလင်းသိမြင်နိုင်သော်လည်း အမှန်တကယ်အားဖြင့် အလေးချိန်နှင့် အရပ်ကြားရှိ ဤဆက်စပ်မှုကို တွက်ချက်ရန်အတွက် linear regression ကိုအသုံးပြုရန် လိုအပ်ပါသည်။

linear regression ကိုသုံးပြီး၊ ကျွန်ုပ်တို့၏ဒေတာကို “ အံကိုက်” အကောင်းဆုံးမျဉ်းကို ရှာတွေ့နိုင်ပါသည်။ ဤမျဉ်းအား အနိမ့်ဆုံး လေးထောင့် ဆုတ်ယုတ်မှုမျဉ်း ဟု လူသိများပြီး အလေးချိန်နှင့် အရပ်အမြင့်တို့ကြား ဆက်နွယ်မှုကို နားလည်ရန် ကူညီပေးနိုင်သည်။

အများအားဖြင့်၊ သင်သည် ဤစာကြောင်းအတွက် ညီမျှခြင်းရှာဖွေရန် Microsoft Excel၊ SPSS သို့မဟုတ် ဂရပ်ဖစ်ဂဏန်းတွက်စက်ကဲ့သို့သော ဆော့ဖ်ဝဲလ်ကို အသုံးပြုလိမ့်မည်။

အသင့်တော်ဆုံးမျဉ်းအတွက် ဖော်မြူလာကို ရေးသားထားသည်။

ŷ = b ₀ + b ₁ x

ŷ သည် တုံ့ပြန်မှုကိန်းရှင်၏ ခန့်မှန်းတန်ဖိုးဖြစ်ပြီး၊ b ₀ သည် ကြားဖြတ်ဖြစ်ပြီး b ₁ သည် ဆုတ်ယုတ်ကိန်းနှင့် x သည် ခန့်မှန်းသူကိန်းရှင်၏တန်ဖိုးဖြစ်သည်။

ဆက်စပ်- လက်တွေ့ဘဝတွင် Linear Regression အသုံးပြုခြင်း ဥပမာ 4 ခု

“ အသင့်တော်ဆုံးလိုင်း” ကိုရှာပါ

ဤဥပမာအတွက်၊ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏ဒေတာကို ကိန်းဂဏန်းမျဉ်းကြောင်းဆုတ်ယုတ်မှုဂဏန်းတွက်စက် သို့ ရိုးရှင်းစွာထည့်သွင်းနိုင်ပြီး Calculate ကိုနှိပ်ပါ။

ဂဏန်းပေါင်းစက်သည် အနိမ့်ဆုံး နှစ်ထပ်ဆုတ်ယုတ်မှုမျဉ်းကို အလိုအလျောက် ရှာဖွေသည်-

ŷ = 32.7830 + 0.2001x

ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏ယခင်ဖြန့်ကျက်မှုမှ ချဲ့ထွင်ပြီး ဤစာကြောင်းကို ဂရပ်သို့ထည့်ပါက၊ ၎င်းသည် ပုံသဏ္ဌာန်ဖြစ်သည်။

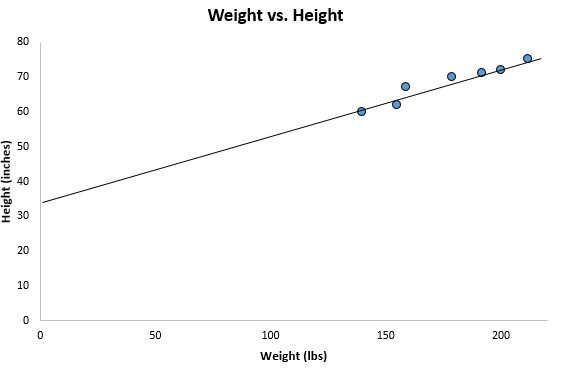
ကျွန်ုပ်တို့၏ဒေတာအချက်များသည် ဤစာကြောင်းတစ်ဝိုက်တွင် မည်သို့ပြန့်ကျဲနေသည်ကို သတိပြုပါ။ အမှန်စင်စစ်၊ ဤစတုရန်းအနိမ့်ဆုံး ဆုတ်ယုတ်မှုမျဉ်းသည် ကျွန်ုပ်တို့ဆွဲနိုင်သည့် ဖြစ်နိုင်ခြေရှိသည့် မျဉ်းများကြားတွင် ကျွန်ုပ်တို့၏ဒေတာနှင့် အသင့်တော်ဆုံးမျဉ်းဖြစ်သည်။

အနည်းဆုံး စတုရန်း ဆုတ်ယုတ်မှုမျဉ်းကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံ

ဤတွင် ဤစတုရန်းအနိမ့်ဆုံး ဆုတ်ယုတ်မှုမျဉ်းကို အဓိပ္ပါယ်ဖွင့်ဆိုပုံဖြစ်ပါသည်- ŷ = 32.7830 + 0.2001x

_b0 = 32.7830 ။ ဆိုလိုသည်မှာ ခန့်မှန်းသူသည် ပြောင်းလဲနိုင်သော အလေးချိန် သုညပေါင်ဖြစ်သောအခါ ခန့်မှန်းထားသော အမြင့်မှာ 32.7830 လက်မဖြစ်သည်။ တစ်ခါတရံ b ₀ ၏တန်ဖိုးကို သိရန် အသုံးဝင်သော်လည်း ဤဥပမာတွင် b _{0 ကို} ကိုယ်အလေးချိန် သုညပေါင်မပေးနိုင်သောကြောင့် အဓိပ္ပာယ်ဖွင့်ဆိုရန် အဓိပ္ပါယ်မရှိပေ။

_b1 = 0.2001 ။ ဆိုလိုသည်မှာ x တွင် တစ်ယူနစ်တိုးခြင်းသည် y တွင် 0.2001 ယူနစ်တိုးခြင်းနှင့် ဆက်စပ်နေသည်။ ဤကိစ္စတွင်၊ တစ်ပေါင်၏အလေးချိန်တိုးလာခြင်းသည် 0.2001 လက်မ အမြင့်နှင့် ဆက်စပ်နေသည်။

လေးထောင့်အနိမ့်ဆုံး ဆုတ်ယုတ်မှုမျဉ်းကို ဘယ်လိုသုံးမလဲ။

ဤအနည်းဆုံး စတုရန်းနှစ်ထပ်မျဉ်းကို အသုံးပြု၍ ကျွန်ုပ်တို့သည် အောက်ပါမေးခွန်းများကို ဖြေနိုင်သည်-

ပေါင် 170 အလေးချိန်ရှိတဲ့သူတစ်ယောက်အတွက် အရပ်ဘယ်လောက်ရှိဖို့ မျှော်လင့်သင့်လဲ။

ဤမေးခွန်းကိုဖြေဆိုရန်၊ ကျွန်ုပ်တို့သည် x အတွက် ကျွန်ုပ်တို့၏ဆုတ်ယုတ်မှုမျဉ်းထဲသို့ 170 ကို ရိုးရှင်းစွာထည့်သွင်းနိုင်ပြီး y အတွက် ဖြေရှင်းနိုင်သည်-

ŷ = 32.7830 + 0.2001(170) = 66.8 လက်မ

ပေါင် 150 အလေးချိန်ရှိတဲ့သူတစ်ယောက်အတွက် အရပ်ဘယ်လောက်ရှိဖို့ မျှော်လင့်သင့်လဲ။

ဤမေးခွန်းကိုဖြေဆိုရန်၊ ကျွန်ုပ်တို့သည် x အတွက် ကျွန်ုပ်တို့၏ဆုတ်ယုတ်မှုမျဉ်းထဲသို့ 150 ကိုထည့်ကာ y အတွက် ဖြေရှင်းနိုင်သည်-

ŷ = 32.7830 + 0.2001(150) = 62.798 လက်မ

သတိပြုရန်- ဤကဲ့သို့သောမေးခွန်းများကိုဖြေဆိုရန် regression equation ကိုအသုံးပြုသောအခါ၊ data set ရှိ ကြိုတင်ခန့်မှန်းကိန်းရှင်၏အကွာအဝေးအတွင်းရှိ ခန့်မှန်းနိုင်သောကိန်းရှင်အတွက် တန်ဖိုးများကိုသာအသုံးပြုရန်သေချာပါစေ။ အနိမ့်ဆုံး စတုရန်း ဆုတ်ယုတ်မှုမျဉ်းကို ထုတ်လုပ်ရန် ကျွန်ုပ်တို့ အသုံးပြုခဲ့သည့် မူလအစ။ ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့၏ဒေတာအစုံရှိအလေးချိန်သည် ၁၄၀ မှ ၂၁၂ ပေါင်ကြားရှိသည်။ ထို့ကြောင့် ကိုယ်အလေးချိန် ၁၄၀ မှ ၂၁၂ ပေါင်ကြားရှိ မျှော်မှန်းထားသော အရပ်နှင့်ပတ်သက်သည့် မေးခွန်းများကို ဖြေဆိုခြင်းသည် အဓိပ္ပာယ်ရှိလှသည်။

ကိန်းဂဏန်း ဆုံးဖြတ်ခြင်း။

အနိမ့်ဆုံး နှစ်ထပ်ဆုတ်ယုတ်မျဉ်းကြောင်း မည်မျှ ကောင်းစွာ တိုင်းတာရန် နည်းလမ်းတစ်ခုမှာ ဒေတာအား ဆုံးဖြတ်ခြင်း၏ ဖော်ကိန်းကို အသုံးပြုခြင်းဖြစ်ပြီး R ^{2 ကို} ကိုယ်စားပြုသည်။

ဆုံးဖြတ်ခြင်း၏ ကိန်းဂဏန်းသည် ခန့်မှန်းသူကိန်းရှင်ဖြင့် ရှင်းပြနိုင်သည့် တုံ့ပြန်မှုကိန်းရှင်၏ ကွဲလွဲမှုအချိုးအစားဖြစ်သည်။

အဆုံးအဖြတ်ပေးသောကိန်းဂဏန်းသည် 0 မှ 1 အထိ ကွဲပြားနိုင်သည်။ 0 တန်ဖိုးသည် ခန့်မှန်းသူကိန်းရှင်က လုံးဝရှင်းပြမရနိုင်သော တုံ့ပြန်မှုကိန်းရှင်ကို ညွှန်ပြသည်။ 1 ၏တန်ဖိုးသည် တုံ့ပြန်မှုကိန်းရှင်အား ကြိုတင်ခန့်မှန်းကိန်းရှင်မှ အမှားအယွင်းမရှိဘဲ စုံလင်စွာရှင်းပြနိုင်သည်ကို ညွှန်ပြသည်။

0 နှင့် 1 အကြား R ² သည် တုံ့ပြန်မှုကိန်းရှင်အား ခန့်မှန်းသူကိန်းရှင်က ရှင်းပြနိုင်သည့်အတိုင်းအတာကို ညွှန်ပြသည်။ ဥပမာအားဖြင့်၊ 0.2 ၏ R ² သည် တုံ့ပြန်မှုကိန်းရှင်ရှိ ကွဲလွဲမှု၏ 20% ကို ခန့်မှန်းသူကိန်းရှင်က ရှင်းပြနိုင်သည်၊ 0.77 ၏ R ² သည် တုံ့ပြန်မှုကိန်းရှင်တွင် ကွဲလွဲမှု 77% ကို ခန့်မှန်းသူကိန်းရှင်က ရှင်းပြနိုင်သည်။

ကျွန်ုပ်တို့၏ယခင်ရလဒ်တွင် ကျွန်ုပ်တို့သည် 0.9311 ၏ R ² ကိုရရှိထားပြီး၊ အမြင့်ပြောင်းလဲမှု၏ 93.11% ကို အလေးချိန်ကြိုတင်ခန့်မှန်းကိန်းရှင်ဖြင့် ရှင်းပြနိုင်သည်ကို သတိပြုပါ။

ကိုယ်အလေးချိန်သည် အရပ်မြင့်ခြင်းအတွက် အလွန်ကောင်းမွန်သော ညွှန်ပြချက်တစ်ခုဖြစ်ကြောင်း ၎င်းကပြောသည်။

Linear Regression ယူဆချက်

linear regression model ၏ ရလဒ်များ မှန်ကန်ပြီး ယုံကြည်စိတ်ချရစေရန်၊ အောက်ပါ ယူဆချက်လေးခုနှင့် ကိုက်ညီကြောင်း စစ်ဆေးရပါမည်။

1. Linear ဆက်ဆံရေး- လွတ်လပ်သော variable, x နှင့် dependent variable, y တို့ကြားတွင် linear ဆက်နွယ်မှုရှိပါသည်။

2. လွတ်လပ်ရေး- အကြွင်းအကျန်များသည် သီးခြားဖြစ်သည်။ အထူးသဖြင့်၊ အချိန်စီးရီးဒေတာတွင် တစ်ဆက်တည်းကျန်နေသည့်အရာများကြား ဆက်စပ်မှုမရှိပါ။

3. Homoscedasticity- ကျန်အကြွင်းများသည် x အဆင့်တစ်ခုစီတွင် အဆက်မပြတ်ကွဲလွဲမှုရှိသည်။

4. Normality- မော်ဒယ်အကြွင်းအကျန်များကို ပုံမှန်အတိုင်း ဖြန့်ဝေပါသည်။

အကယ်၍ ဤယူဆချက်များထဲမှ တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ယူဆချက်များနှင့် မကိုက်ညီပါက၊ ကျွန်ုပ်တို့၏ မျဉ်းကြောင်းဆုတ်ယုတ်မှု၏ ရလဒ်များသည် ယုံကြည်စိတ်ချရသော သို့မဟုတ် လွဲမှားခြင်းပင် ဖြစ်နိုင်ပါသည်။

ယူဆချက်တစ်ခုစီ၏ ရှင်းလင်းချက်၊ ယူဆချက်နှင့် ကိုက်ညီခြင်း ရှိ၊ မရှိ ဆုံးဖြတ်နည်းနှင့် ယူဆချက် မပြည့်မီပါက ဘာလုပ်ရမည်ကို ဤဆောင်းပါးကို ကိုးကားပါ။