Logistic regression အမျိုးအစား ၃ မျိုး (ဥပမာများ အပါအဝင်)

Logistic regression သည် တုံ့ပြန်မှု မပြောင်းလဲနိုင်သော အမျိုးအစားအလိုက် ဆုတ်ယုတ်မှုပုံစံကို ရည်ညွှန်းသည်။

Logistic regression model အမျိုးအစားသုံးမျိုး ရှိပါသည်။

• Binary logistic regression : တုံ့ပြန်မှု variable သည် အမျိုးအစားနှစ်ခုထဲမှ တစ်ခုသာ သက်ဆိုင်ပါသည်။
• Multinomial logistic regression : တုံ့ပြန်မှုကိန်းရှင်သည် အမျိုးအစားသုံးမျိုး သို့မဟုတ် ထို့ထက်ပိုသော အမျိုးအစားများထဲမှ တစ်ခုသို့ ကျဆင်းနိုင်ပြီး အမျိုးအစားများကြားတွင် သဘာဝအတိုင်း စီစဥ်ထားခြင်းမရှိပါ။
• Ordinal logistic regression : တုံ့ပြန်မှု variable သည် အမျိုးအစား သုံးခု သို့မဟုတ် ထို့ထက်ပိုသော အမျိုးအစားများထဲမှ တစ်ခုသို့ ကျဆင်းနိုင်ပြီး အမျိုးအစားများကြားတွင် သဘာဝအတိုင်း စီစစ်မှု ရှိပါသည် ။

အောက်ပါဇယားသည် ဤကွဲပြားမှုများကို အကျဉ်းချုပ်ဖော်ပြသည်-

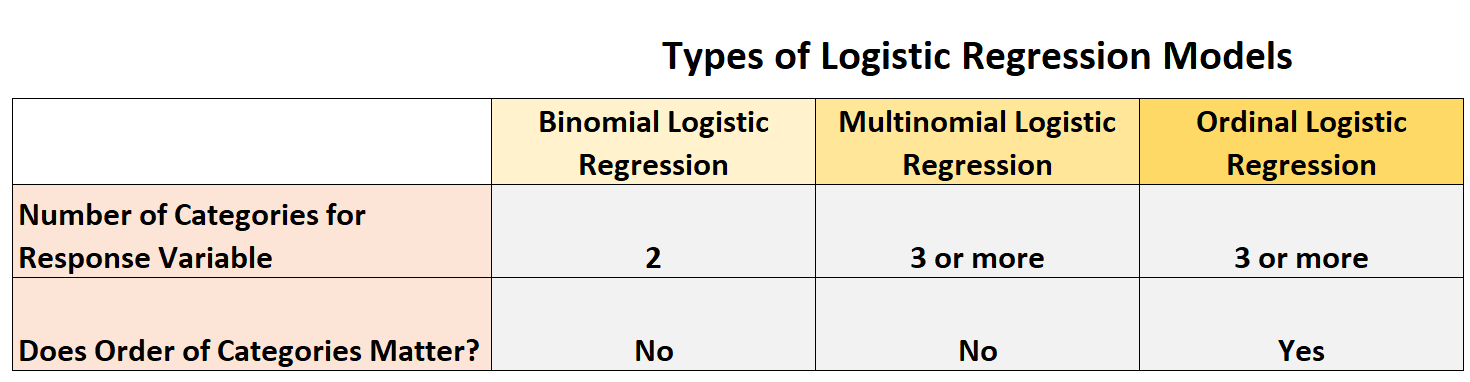
ဤကျူတိုရီရယ်သည် တစ်ခုချင်းစီ၏ နမူနာများနှင့်အတူ ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုပုံစံ အမျိုးအစားတစ်ခုစီ၏ အတိုချုံးရှင်းလင်းချက်ကို ပေးပါသည်။

အမျိုးအစား နံပါတ် 1- ဒွိထောက်လှမ်းဆုတ်ယုတ်မှု

Binary logistic regression မော်ဒယ်များ သည် တုံ့ပြန်မှု variable တွင် အမျိုးအစား နှစ်ခုသာ ကျရောက်နိုင်သော ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှု အမျိုးအစားတစ်ခုဖြစ်သည်။

ဤသည်မှာ ဥပမာအချို့ဖြစ်သည်။

ဥပမာ 1- NBA မူကြမ်း

အားကစားဒေတာသိပ္ပံပညာရှင်တစ်ဦးသည် NBA သို့ ကောလိပ်ဘတ်စကက်ဘောကစားသမားတစ်ဦးကို ရေးဆွဲမည့်ဖြစ်နိုင်ခြေကို ခန့်မှန်းရန် ခန့်မှန်းကိန်းရှင် (1) မှတ်၊ (2) ပြန်ပြန်ကြားချက် (3) တို့ကို အသုံးပြုလိုသည်ဆိုပါစို့။

တုံ့ပြန်မှု variable အတွက် ဖြစ်နိုင်ချေ ရလဒ် နှစ်ခုသာ (ရေးထားသည် သို့မဟုတ် မရေးထား) ဖြစ်သောကြောင့် ဒေတာသိပ္ပံပညာရှင်သည် binomial logistic regression model ကို အသုံးပြုမည်ဖြစ်သည်။

ဥပမာ 2- Spam သိရှိခြင်း

ကုမ္ပဏီတစ်ခုသည် ပေးထားသောအီးမေးလ်သည် spam ဖြစ်နိုင်ခြေကို ခန့်မှန်းရန် (၁) စကားလုံးအရေအတွက်နှင့် (2) မူရင်းနိုင်ငံကို အသုံးပြုလိုသည်ဆိုပါစို့။

တုံ့ပြန်မှုကိန်းရှင်အတွက် ဖြစ်နိုင်ချေ ရလဒ်နှစ်ခု (စပမ်း သို့မဟုတ် စပမ်းမဟုတ်သော) သာရှိသောကြောင့် ကုမ္ပဏီသည် binomial logistic regression model ကို အသုံးပြုမည်ဖြစ်သည်။

အမျိုးအစား နံပါတ် 2- ဘက်စုံ ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှု

Multinomial logistic regression မော်ဒယ်များ သည် တုံ့ပြန်မှုမပြောင်းလဲနိုင်သော အမျိုးအစားသုံးမျိုး သို့မဟုတ် ထို့ထက်ပိုသော အမျိုးအစားများသို့ ကျရောက်နိုင်ပြီး အမျိုးအစားများကြားတွင် သဘာဝအတိုင်း စီစစ်ခြင်းမရှိသော ထောက်ပံ့ပို့ဆောင်ရေးဆုတ်ယုတ်မှုအမျိုးအစားတစ်ခုဖြစ်သည်။

ဤသည်မှာ ဥပမာအချို့ဖြစ်သည်။

ဥပမာ 1- နိုင်ငံရေးဦးစားပေး

နိုင်ငံရေးသိပ္ပံပညာရှင်တစ်ဦးသည် မတူညီသောသမ္မတလောင်းလေးယောက်အနက်မှ တစ်ဦးကို မဲပေးမည့်ဖြစ်နိုင်ခြေကို ခန့်မှန်းရန် (၁) နှစ်ဝင်ငွေနှင့် ပညာရေး (၂) နှစ်တို့ကို ခန့်မှန်းရန် ကိန်းရှင်များကို အသုံးပြုလိုသည်ဆိုပါစို့။

တုံ့ပြန်မှုကိန်းရှင်အတွက် ဖြစ်နိုင်ခြေရှိသော ရလဒ်နှစ်ခုထက်ပို၍ (အလားအလာရှိသော ကိုယ်စားလှယ်လောင်း လေးဦးရှိသည်) ရှိပြီး ရလဒ်များကြားတွင် သဘာဝအတိုင်း စီစဥ်ထားခြင်း မရှိသောကြောင့် နိုင်ငံရေးသိပ္ပံပညာရှင်သည် ဘက်စုံသုံး ထောက်လှမ်းမှုဆိုင်ရာ ဆုတ်ယုတ်မှုပုံစံကို အသုံးပြုမည်ဖြစ်သည်။

ဥပမာ 2- အားကစား ဦးစားပေး

အားကစားသုံးသပ်သူတစ်ဦးသည် တစ်ပတ်လျှင် ကြည့်ရှုသည့် ရုပ်မြင်သံကြား (၁) နာရီနှင့် (၂) နှစ်အရွယ်တွင် ဘတ်စကက်ဘော၊ ဘောလုံး သို့မဟုတ် ဘေ့စ်ဘောတို့ကို ၎င်းတို့၏ စိတ်ကြိုက်အားကစားအဖြစ် ရွေးချယ်မည့် ဖြစ်နိုင်ခြေကို ခန့်မှန်းရန် အားကစားသုံးသပ်သူတစ်ဦးက အသုံးပြုလိုသည်ဆိုပါစို့။

တုံ့ပြန်မှုပြောင်းလဲနိုင်သောအတွက် ဖြစ်နိုင်ချေ ရလဒ်နှစ်ခုထက်ပို၍ (အားကစားသုံးမျိုးရှိသည်) ဖြစ်သောကြောင့် အားကစားသုံးသပ်သူသည် ဘက်စုံသုံး ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုပုံစံကို အသုံးပြုမည်ဖြစ်သည်။

အမျိုးအစား နံပါတ် ၃- ပုံမှန် ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှု

Ordinal logistic regression မော်ဒယ်များ သည် တုံ့ပြန်မှုမပြောင်းလဲနိုင်သော အမျိုးအစားသုံးမျိုး သို့မဟုတ် ထို့ထက်ပိုသော အမျိုးအစားများအတွင်း ကျရောက်နိုင်ပြီး အမျိုးအစားများကြားတွင် သဘာဝအတိုင်း စီစဥ်ပေး သည့် ထောက်ပံ့ပို့ဆောင်ရေးဆုတ်ယုတ်မှုအမျိုးအစားတစ်ခုဖြစ်သည်။

ဤသည်မှာ ဥပမာအချို့ဖြစ်သည်။

ဥပမာ 1- ကျောင်းအကဲဖြတ်ချက်များ

ကောလိပ်အကြံပေးတစ်ဦးသည် “ဆိုးရွားသော”၊ “အလယ်အလတ်” ဟု အမျိုးအစားခွဲခြားနိုင်သော ကောလိပ်တစ်ခုသို့ ဝင်ရောက်နိုင်ခြေကို ခန့်မှန်းရန် ကောလိပ်အကြံပေးတစ်ဦးသည် (၁) GPA၊ (၂) ACT ရမှတ်နှင့် (၃) SAT ရမှတ်များကို အသုံးပြုလိုသည်ဆိုပါစို့၊ . »၊ “ ကောင်း” သို့မဟုတ် “ ကြီးမြတ်” ။

တုံ့ပြန်မှုကိန်းရှင်အတွက် ဖြစ်နိုင်ခြေရှိသော ရလဒ်နှစ်ခုထက်ပို၍ (ကျောင်းအရည်အသွေး အမျိုးအစား လေးမျိုးပါရှိသည်) နှင့် ရလဒ်များကြားတွင် သဘာဝအတိုင်း စီစဥ်ထား သောကြောင့် ၊ ကျောင်းအတိုင်ပင်ခံပုဂ္ဂိုလ်သည် သာမန်ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုပုံစံကို အသုံးပြုမည်ဖြစ်သည်။

ဥပမာ 2- ရုပ်ရှင် အဆင့်သတ်မှတ်ချက်များ

ရုပ်ရှင်ဝေဖန်ရေးဆရာတစ်ဦးသည် ပေးထားသောရုပ်ရှင်သည် အဆင့်သတ်မှတ်ချက် 1 နှင့် 10 ကြား ရရှိမည့်ဖြစ်နိုင်ခြေကို ခန့်မှန်းရန် ခန့်မှန်းပေးသည့်ကိန်းရှင်များ (1) စုစုပေါင်းလည်ပတ်ချိန်နှင့် (2) အမျိုးအစားကို အသုံးပြုလိုသည်ဆိုပါစို့။

တုံ့ပြန်မှုမပြောင်းလဲနိုင်သော ဖြစ်နိုင်ခြေရှိသော ရလဒ်နှစ်ခုထက်ပို၍ (ဖြစ်နိုင်ချေ အဆင့်သတ်မှတ်ချက် 10 ရှိသည်) နှင့် ရလဒ်များကြားတွင် သဘာဝအတိုင်း စီစဥ်ထား သော ကြောင့်၊ ရုပ်ရှင်ဝေဖန်ရေးဆရာသည် သာမန်ထောက်ပံ့ပို့ဆောင်ရေးဆိုင်ရာ ဆုတ်ယုတ်မှုပုံစံကို အသုံးပြုမည်ဖြစ်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုပုံစံများအကြောင်း နောက်ထပ်အသေးစိတ်အချက်အလက်များကို ပေးဆောင်သည်-

Logistic Regression နိဒါန်း
ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှု၏ ယူဆချက် (၆) ခု
4 လက်တွေ့ဘဝတွင် Logistic Regression ကိုအသုံးပြုခြင်း၏နမူနာများ