Lorenz မျဉ်းကွေး

ဤဆောင်းပါးတွင် Lorenz မျဉ်းကွေးသည် အဘယ်အရာနှင့် ၎င်းကိုအသုံးပြုကြောင်း ရှင်းပြထားသည်။ လူဦးရေ၏ Lorenz မျဉ်းကွေးကို မည်သို့ဖန်တီးရမည်ကို သင်ရှာဖွေတွေ့ရှိမည်ဖြစ်ပြီး၊ ထို့အပြင် လေ့ကျင့်ခန်းအဆင့်ဆင့်ကို ဖြေရှင်းထားသည်ကို သင်တွေ့မြင်နိုင်မည်ဖြစ်သည်။ နောက်ဆုံးတွင် Lorenz မျဉ်းကွေး၏ဂုဏ်သတ္တိများနှင့် Gini အညွှန်းကိန်းနှင့်ဆက်စပ်မှုကိုတင်ပြသည်။

Lorenz မျဉ်းကွေးဆိုတာဘာလဲ။

Lorenz မျဉ်းကွေး သည် နယ်မြေတစ်ခု၏ လူဦးရေ၏ စီးပွားရေးမညီမျှမှုများကို ဂရပ်ဖစ်ဖော်ပြသည်။ တစ်နည်းဆိုရသော် Lorenz မျဉ်းကွေးသည် နယ်မြေတစ်ခုမှ ဝင်ငွေခွဲဝေမှုတွင် မညီမျှမှုများကို ခွဲခြမ်းစိတ်ဖြာနိုင်စေသည့် မျဉ်းကွေးတစ်ခုဖြစ်သည်။

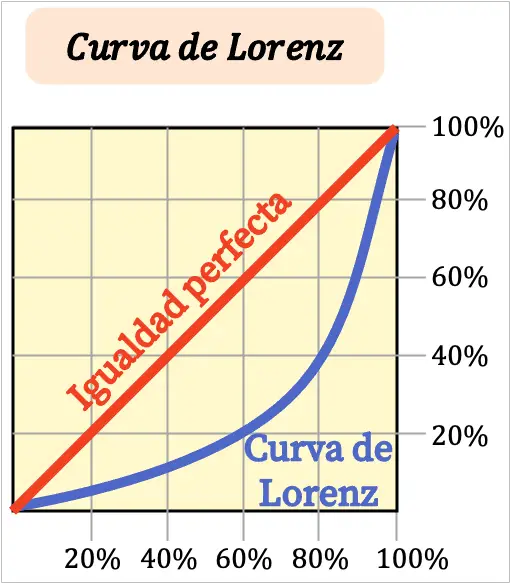
Lorenz မျဉ်းကွေးကို ဖြောင့်လေလေ၊ ရပ်ကွက်၏ ၀င်ငွေသည် ပိုမိုမျှတလေဖြစ်သည်။ အခြားတစ်ဖက်တွင်၊ Lorenz မျဉ်းကွေးကို ပိုကွေးလေ၊ ဝင်ငွေမမျှတလေလေဖြစ်သည်။

ပုံမှန်အားဖြင့် Lorenz မျဉ်းကွေး၏ axes များကို ရာခိုင်နှုန်းများအဖြစ် ဖော်ပြသည်။ ဂရပ်၏ X ဝင်ရိုးသည် လူဦးရေ ရာခိုင်နှုန်းကို ကိုယ်စားပြုပြီး အခြားတစ်ဖက်တွင်၊ Y ဝင်ရိုးသည် ဝင်ငွေရာခိုင်နှုန်းကို ပြသသည်။

Lorenz မျဉ်းကွေးကို 1905 ခုနှစ်တွင် 20 ရာစု၏ အလွန်အရေးကြီးသော အမေရိကန်စီးပွားရေးပညာရှင် Max Otto Lorenz မှ တီထွင်ခဲ့သည်။

Lorenz မျဉ်းကွေးကို တွက်နည်း

Lorenz မျဉ်းကွေး၏ အဓိပ္ပာယ်ဖွင့်ဆိုချက်ကို သိရှိပြီးသည်နှင့် ဤကိန်းဂဏန်းမျဉ်းကွေးကို မည်ကဲ့သို့ တွက်ချက်ထားသည်ကို ကျွန်ုပ်တို့ မြင်တွေ့ရမည်ဖြစ်သည်။ Lorenz မျဉ်းကွေးကို သတ်မှတ်ရန် ဖော်မြူလာရှိသည်ကို သတိပြုသင့်သော်လည်း လက်တွေ့တွင် ၎င်းကို ယေဘုယျအားဖြင့် အသုံးမပြုပါ။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် ဥပမာတစ်ခုကို တစ်ဆင့်ပြီးတစ်ဆင့် ဖြေရှင်းမည်ဖြစ်သောကြောင့် ၎င်းကို မည်သို့လုပ်ဆောင်သည်ကို သင်ကြည့်ရှုနိုင်မည်ဖြစ်သည်။

• အောက်ပါဇယားတွင်ဖော်ပြထားသောဝင်ငွေ၏လူဦးရေ၏ Lorenz မျဉ်းကွေးကိုကိုယ်စားပြုသည်-

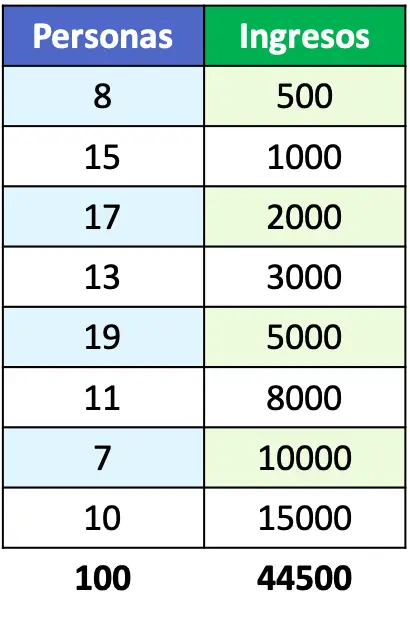
ပြဿနာထုတ်ပြန်ချက်သည် Lorenz မျဉ်းကွေးလုပ်ဆောင်ချက်ကို ဥပမာပေးလျှင်၊ ဂရပ်တစ်ခုပေါ်ရှိ လုပ်ဆောင်ချက်ကို ကျွန်ုပ်တို့ တိုက်ရိုက်ကိုယ်စားပြုနိုင်သည်။ ဒါပေမဲ့ ဒီအခြေအနေမှာ သူတို့က ကျွန်တော်တို့ကို လူဦးရေဝင်ငွေကိုပဲ ပေးတဲ့အတွက် လူအုပ်စုတစ်ခုစီရဲ့ ရာခိုင်နှုန်းကို တွက်ချက်ရမယ်။

ထို့ကြောင့်၊ လူအရေအတွက်နှင့် ဝင်ငွေ၏ ရာခိုင်နှုန်းများကို ဆုံးဖြတ်ရန်၊ လူဦးရေ variable အတွက် ဇယားတွင် ကော်လံနှစ်ခုကို ထည့်ရပါမည်။

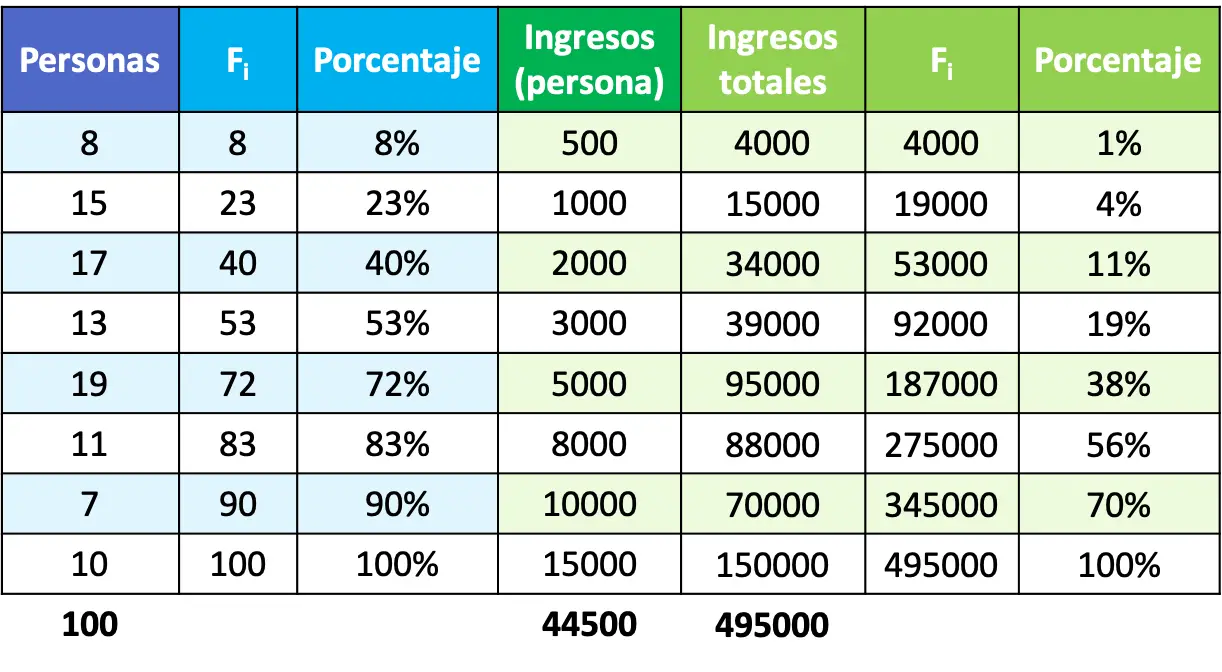
• စုဆောင်းထားသော absolute frequency (F _i ) ပါသော ကော်လံ။
• စုစည်းမှု ရာခိုင်နှုန်းနှင့် သက်ဆိုင်သည့် ဒုတိယကော်လံတစ်ခု၊ လူစုစုပေါင်းအရေအတွက်ဖြင့် စုစည်းမှု ပကတိအကြိမ်ရေကို ပိုင်းခြား၍ တွက်ချက်သည်။

အခြားတစ်ဖက်တွင်၊ ကျွန်ုပ်တို့သည် ၀င်ငွေပြောင်းလဲမှုအတွက် ကော်လံသုံးခုကို ထည့်ရပါမည်-

• စုစုပေါင်းဝင်ငွေကို တွက်ချက်သည့်ကော်လံ၊ လူတစ်ဦးစီရရှိသည့်ဝင်ငွေဖြင့် လူအရေအတွက်၏ ထုတ်ကုန်နှင့် ညီမျှသည်။
• စုစုပေါင်းဝင်ငွေ၏ စုဆောင်းထားသော ပကတိအကြိမ်ရေ (F _i ) နှင့် တစ်စက္ကန့်။
• ယခင်ကော်လံကို လူဦးရေစုစုပေါင်း၏ဝင်ငွေဖြင့် ပိုင်းခြားခြင်းဖြင့် ဆုံးဖြတ်ထားသော စုဆောင်းရာခိုင်နှုန်းများ ပါဝင်သော တတိယကော်လံ။

နောက်ဆုံးတွင်၊ ယခု ကျွန်ုပ်တို့သည် ရာခိုင်နှုန်းများကို တွက်ချက်ပြီး ကျန်အရာအားလုံးမှာ ဂရပ်တစ်ခုပေါ်တွင် အမှတ်များကို ဆွဲချပြီး Lorenz မျဉ်းကွေးကို ပေါင်းစပ်ရန်ဖြစ်သည်။ X ဝင်ရိုးသည် လူဦးရေ၏ ရာခိုင်နှုန်းဖြစ်ပြီး Y ဝင်ရိုးသည် ဝင်ငွေရာခိုင်နှုန်းဖြစ်ကြောင်း သတိရပါ။

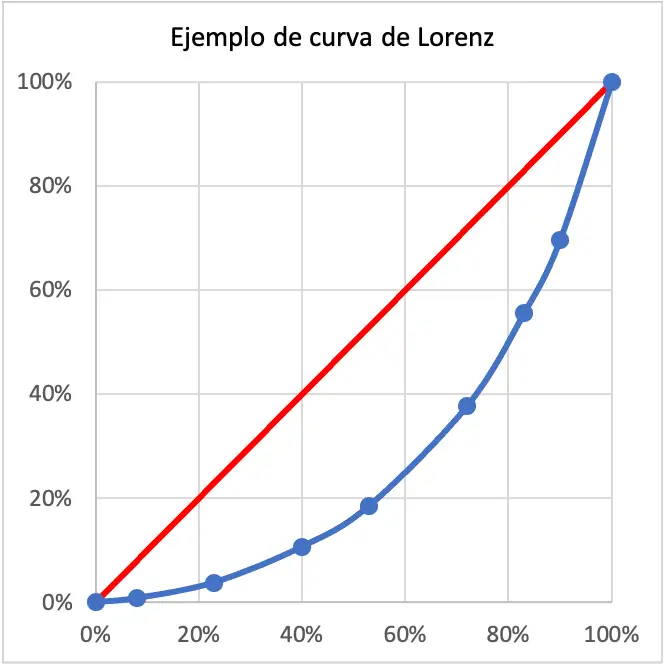
ဤကိစ္စတွင်၊ Lorenz မျဉ်းကွေးသည် အလွန်ကျယ်ပြန့်သောကြောင့် လေ့လာထားသော လူဦးရေ၏ဝင်ငွေသည် အလွန်မညီမျှပေ။ တကယ်တော့ Lorenz မျဉ်းကွေးဟာ ပြီးပြည့်စုံတဲ့ တန်းတူညီမျှမှုကို ကိုယ်စားပြုတဲ့ အနီရောင်မျဉ်းနဲ့ အလွန်ဝေးပါတယ်။

Lorenz မျဉ်းကွေး၏အဓိပ္ပာယ်ဖွင့်ဆိုချက်

ဤအပိုင်းသည် လူဦးရေ၏ Lorenz မျဉ်းကွေးကို မည်သို့အနက်ပြန်ဆိုရမည်ကို ရှင်းပြသည်၊ အကြောင်းမှာ ၎င်းကို ဂရပ်ဖစ်လုပ်နည်းသိသည့်အပြင်၊ ၎င်းကို ဆိုလိုသည်ကိုလည်း နားလည်ရန် လိုအပ်ပါသည်။

Lorenz မျဉ်းကွေးသည် ရပ်ကွက်တစ်ခု၏ စုစုပေါင်းဝင်ငွေ၏ ရာခိုင်နှုန်းတစ်ခု ပိုင်ဆိုင်သည့် လူဦးရေ၏ ရာခိုင်နှုန်းကို ညွှန်ပြသည်။ ဥပမာအားဖြင့်၊ အထက်တွင်ပြသထားသော Lorenz မျဉ်းကွေးတွင်၊ လူဦးရေ၏ 40% သည် လူဦးရေအားလုံး၏ 11% ဝင်ငွေရှိသည်။ အဲဒီတော့ နယ်မြေက အရမ်းမညီဘူး။

ထို့ကြောင့် Lorenz မျဉ်းကွေးသည် နိုင်ငံတစ်ခု သို့မဟုတ် နယ်မြေနေထိုင်သူများကြားတွင် တန်းတူညီမျှမှု သို့မဟုတ် ဝင်ငွေမညီမျှမှုကို ကိုယ်စားပြုသည် ။ ပြီးပြည့်စုံသော တန်းတူညီမျှမှုကို ညွှန်ပြသော မျဉ်းကြောင်းမှ ကျွန်ုပ်တို့ ဝေးကွာလေလေ၊ လူဦးရေ၏ ဝင်ငွေသည် ပို၍ မညီမျှဟု ဆိုလိုပါသည်။ အခြားတစ်ဖက်တွင်၊ Lorenz မျဉ်းကွေးသည် ညာဘက်သို့ ပိုနီးကပ်လေလေ၊ လူဦးရေ၏ ၀င်ငွေကို ပိုမိုမျှတစွာ ခွဲဝေပေးကြောင်း အဓိပ္ပါယ်သက်ရောက်လေလေဖြစ်သည်။

ထို့အပြင်၊ အကယ်၍ Lorenz မျဉ်းကွေးတစ်ခုသည် ဂရပ်တစ်လျှောက်ရှိ အခြား Lorenz မျဉ်းကွေးအထက်တွင် ရှိနေပါက၊ ဆိုလိုသည်မှာ ပထမလူဦးရေ၏ ၀င်ငွေသည် ဒုတိယအရေအတွက်ထက် ပိုညီမျှနေသည်။

Lorenz မျဉ်းကွေးနှင့် Gini ကိန်းဂဏန်း

ဆောင်းပါးတစ်လျှောက်လုံးတွင် ရှင်းပြထားသည့်အတိုင်း Lorenz မျဉ်းကွေးသည် ရပ်ကွက်တစ်ခု၏ ၀င်ငွေကို မည်သို့ခွဲဝေပုံနှင့် နယ်မြေတစ်ခု မည်မျှမညီမျှကြောင်း ဂရပ်ဖစ်ပြသည်။

အခြားတစ်ဖက်တွင်၊ Gini အညွှန်းကိန်းဟုလည်း ခေါ်သော Gini coefficient သည် နယ်မြေတစ်ခု၏ စီးပွားရေးမညီမျှမှုကို ဂဏန်းများဖြင့် ညွှန်ပြသည်။

ထို့ကြောင့် Lorenz မျဉ်းကွေးနှင့် Gini coefficient ကို ချိတ်ဆက်ထားသည်။ အမှန်မှာ၊ နိုင်ငံတစ်ခု၏ Gini coefficient ကို ၎င်း၏ Lorenz မျဉ်းကွေးမှ တွက်ချက်နိုင်သည်။ အောက်ပါဆောင်းပါးတွင် သင်ဤကိုပြုလုပ်နည်းကို ကြည့်ရှုနိုင်သည်-

Lorenz မျဉ်းကွေး၏ ဂုဏ်သတ္တိများ

Lorenz မျဉ်းကွေးတွင် အောက်ပါဂုဏ်သတ္တိများရှိသည်။

• Lorenz မျဉ်းကွေးသည် အမြဲတမ်း အမှတ် (0,0) တွင် စတင်ပြီး (100,100) ဖြင့် အဆုံးသတ်သည်။
• နမူနာဆိုလိုရင်းမှာ သုညဖြစ်လျှင် Lorenz မျဉ်းကွေးကို သတ်မှတ်မထားပါ။
• Lorenz မျဉ်းကွေးသည် ပြီးပြည့်စုံသော တန်းတူညီမျှမှုမျဉ်းအထက် ဂရပ်ပေါ်တွင် မပေါ်နိုင်ပါ။
• ဝင်ငွေက အနုတ်လက္ခဏာမဖြစ်နိုင်ဘူးလို့ ယူဆရင် Lorenz မျဉ်းကွေးက အမြဲတမ်းတိုးနေတယ်။