Mann-whitney u စမ်းသပ်မှု
Mann-Whitney U စမ်းသပ်မှု (တစ်ခါတစ်ရံ Wilcoxon rank sum test ဟုခေါ်သည်) ကိုနမူနာဖြန့်ဝေမှုများကို ပုံမှန်မဖြန့်ဝေဘဲနှင့် နမူနာအရွယ်အစားများသည် သေးငယ်သည် (n <30) တွင် သီးခြားနမူနာနှစ်ခုကြား ကွာခြားချက်များကို နှိုင်းယှဉ်ရန် အသုံးပြုသည်။
လွတ်လပ်သောနမူနာနှစ်ခု t စမ်းသပ်မှု ၏ parametric ညီမျှခြင်းဟု ယူဆသည်။
ဤသည်မှာ Mann-Whitney U စမ်းသပ်မှုကို သင်အသုံးပြုသည့်အခါ ဥပမာအချို့ဖြစ်သည်။
- တက္ကသိုလ် A မှ ဘွဲ့ရငါးဦး၏ လစာနှင့် တက္ကသိုလ် B ဘွဲ့ရငါးဦး၏ လစာတို့ကို နှိုင်းယှဉ်လိုသည်။ လစာများကို ပုံမှန်ခွဲဝေပေးမည်မဟုတ်ပါ။
- ကိုယ်အလေးချိန်ကျခြင်းအတွက် အုပ်စုနှစ်စုကွဲပြားမှုရှိမရှိ သိလိုပါသည်- အစားအသောက် A ကိုသုံးသော လူ ၁၂ ဦးနှင့် အစားအသောက် B သုံးစွဲသူ ၁၀ ဦးတို့ဖြစ်သည်။ အဆိုပါကိုယ်အလေးချိန်ကို ပုံမှန်မဖြန့်ဝေပါ။
- အတန်း A ရှိ ကျောင်းသား ၈ ဦး၏ ရမှတ်များသည် အတန်း B ရှိ ကျောင်းသား ၇ ဦးနှင့် ကွာခြားမှုရှိမရှိ သိလိုပါသည်။ ရမှတ်များကို ပုံမှန်အတိုင်း ခွဲဝေပေးမည်မဟုတ်ပါ။
ဥပမာတစ်ခုစီတွင် အုပ်စုနှစ်ခုကို နှိုင်းယှဉ်လိုသည်၊ နမူနာဖြန့်ဝေမှုများသည် ပုံမှန်မဟုတ်ပါ၊ နမူနာအရွယ်အစားများသည် သေးငယ်ပါသည်။
ထို့ကြောင့် အောက်ဖော်ပြပါ ယူဆချက်များနှင့် ပြည့်မီသရွေ့ Mann-Whitney U စမ်းသပ်မှုသည် သင့်လျော်ပါသည်။
Mann-Whitney U စမ်းသပ်မှု ယူဆချက်
Mann-Whitney U စမ်းသပ်မှု မလုပ်ဆောင်မီ၊ အောက်ပါ ယူဆချက်လေးခုနှင့် ကိုက်ညီကြောင်း သေချာစေရမည်။
- သာမာန် သို့မဟုတ် စဉ်ဆက်မပြတ်- သင်ခွဲခြမ်းစိတ်ဖြာသော ကိန်းရှင်သည် ပုံမှန် သို့မဟုတ် ဆက်တိုက်ဖြစ်သည်။ ပုံမှန်မပြောင်းလဲနိုင်သော ဥပမာများတွင် Likert ပစ္စည်းများပါဝင်သည် (ဥပမာ၊ “ပြင်းထန်စွာသဘောမတူ” မှ “ပြင်းထန်စွာသဘောတူသည်” အထိ 5-မှတ်စကေးတစ်ခု)။ စဉ်ဆက်မပြတ်ပြောင်းလဲနိုင်သောနမူနာများတွင် အရပ် (လက်မဖြင့်တိုင်းတာခြင်း)၊ ကိုယ်အလေးချိန် (ပေါင်ဖြင့်တိုင်းတာခြင်း) သို့မဟုတ် စမ်းသပ်မှုရမှတ်များ (0 မှ 100 အထိတိုင်းတာသည်) ပါဝင်သည်။
- လွတ်လပ်ရေး- အဖွဲ့နှစ်ဖွဲ့လုံးမှ ရှုမြင်ချက်အားလုံးသည် တစ်ခုနှင့်တစ်ခု သီးခြားဖြစ်သည်။
- ပုံသဏ္ဍာန်- အုပ်စုနှစ်ခုအတွက် ဖြန့်ဝေမှုပုံစံများသည် ခန့်မှန်းခြေအားဖြင့် တူညီသည်။
အဆိုပါယူဆချက်များနှင့်ကိုက်ညီပါက Mann-Whitney U စမ်းသပ်မှုပြုလုပ်နိုင်သည်။
Mann-Whitney U Test ကို ဘယ်လိုလုပ်ဆောင်မလဲ။
Mann-Whitney U စမ်းသပ်မှုပြုလုပ်ရန်၊ ကျွန်ုပ်တို့သည် စံငါးဆင့်ယူဆချက်စမ်းသပ်ခြင်းလုပ်ငန်းစဉ်ကို လိုက်နာသည်-
1. ယူဆချက်များကို ဖော်ပြပါ။
ကိစ္စအများစုတွင်၊ Mann-Whitney U စမ်းသပ်မှုကို အမြီးနှစ်ပိုင်းစမ်းသပ်မှုအဖြစ် လုပ်ဆောင်သည်။ null နှင့် အခြားယူဆချက်များအား ပုံစံဖြင့် ရေးသားထားသည်။
H 0 : လူဦးရေ နှစ်ခုသည် ညီမျှသည်။
H a : လူဦးရေနှစ်ခုက မညီဘူး။
2. ယူဆချက်အတွက် အသုံးပြုရန် အရေးပါမှုအဆင့်ကို သတ်မှတ်ပါ။
အရေးပါမှုအဆင့်ကို ဆုံးဖြတ်ပါ။ ဘုံရွေးချယ်မှုများမှာ .01၊ .05၊ နှင့် .1 ဖြစ်သည်။
3. စမ်းသပ်စာရင်းအင်းကိုရှာပါ။
စမ်းသပ်မှုစာရင်းအင်းအား U ဖြင့်ရည်ညွှန်းပြီး အောက်တွင်ဖော်ပြထားသည့်အတိုင်း U 1 နှင့် U 2 ၏သေးငယ်သည်-
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
n 1 နှင့် n 2 သည် နမူနာအရွယ်အစား 1 နှင့် 2 အသီးသီးဖြစ်ပြီး R 1 နှင့် R 2 တို့သည် နမူနာ 1 နှင့် 2 အတွက် အဆင့်များ၏ ပေါင်းလဒ်ဖြစ်သည်။
အောက်ပါနမူနာများသည် ဤစမ်းသပ်မှုစာရင်းအင်းအား မည်သို့ရှာဖွေရမည်ကို အသေးစိတ်ပြသပါမည်။
4. null hypothesis ကို ငြင်းပယ်ခြင်း သို့မဟုတ် ငြင်းပယ်ခြင်းမပြုပါနှင့်။
စမ်းသပ်စာရင်းဇယားကိုအသုံးပြု၍ Mann-Whitney U ဇယားတွင်တွေ့ရှိရသော အရေးပါမှုအဆင့်နှင့် အရေးပါသောတန်ဖိုးအပေါ်အခြေခံ၍ null hypothesis ကို ငြင်းပယ်နိုင်သည်ဖြစ်စေ ဆုံးဖြတ်ပါ။
5. ရလဒ်များကို ဘာသာပြန်ပါ။
မေးသည့်မေးခွန်း၏ ဆက်စပ်မှုတွင် စာမေးပွဲရလဒ်ကို ပြန်ဆိုပါ။
Mann-Whitney U စမ်းသပ်မှု ပြုလုပ်ခြင်း၏ နမူနာများ
အောက်ဖော်ပြပါ ဥပမာများသည် Mann-Whitney U စမ်းသပ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသထားသည်။
ဥပမာ ၁
ဆေးဝါးအသစ်သည် အထိတ်တလန့်တိုက်ခိုက်မှုများကို ကာကွယ်ရန် ထိရောက်မှု ရှိ၊ မရှိ သိလိုပါသည်။ စုစုပေါင်းလူနာ 12 ဦးကို 6 အုပ်စုနှစ်စုခွဲ၍ ဆေးဝါးအသစ် သို့မဟုတ် placebo ကိုလက်ခံရရှိရန်တာဝန်ပေးအပ်သည်။ ထို့နောက် လူနာများသည် တစ်လတာအတွင်း သူတို့ကြုံတွေ့ခဲ့ရသည့် ထိတ်လန့်တိုက်ခိုက်မှုအရေအတွက်ကို မှတ်တမ်းတင်သည်။
ရလဒ်များကို အောက်တွင် ပြထားသည်။
| ဆေးအသစ် | PLACEBO |
|---|---|
| ၃ | ၄ |
| ၅ | ၈ |
| ၁ | ၆ |
| ၄ | ၂ |
| ၃ | ၁ |
| ၅ | ၉ |
ဆေးအုပ်စုအသစ်နှင့် နှိုင်းယှဉ်ပါက placebo အုပ်စုရှိ လူနာများအကြား ထိတ်လန့်တိုက်ခိုက်မှု အရေအတွက် ကွာခြားမှုရှိမရှိ သိရန် Mann-Whitney U စမ်းသပ်မှု ပြုလုပ်ပါ။ သိသာထင်ရှားမှုအဆင့် 0.05 ကိုသုံးပါ။
1. ယူဆချက်များကို ဖော်ပြပါ။
H 0 : လူဦးရေ နှစ်ခုသည် ညီမျှသည်။
H a : လူဦးရေနှစ်ခုက မညီဘူး။
2. ယူဆချက်အတွက် အသုံးပြုရန် အရေးပါမှုအဆင့်ကို သတ်မှတ်ပါ။
ပြဿနာက ကျွန်ုပ်တို့သည် 0.05 ၏ အရေးပါမှုအဆင့်ကို အသုံးပြုသင့်သည်ဟု ဆိုသည်။
3. စမ်းသပ်စာရင်းအင်းကိုရှာပါ။
စမ်းသပ်စာရင်းအင်းသည် U ကိုရည်ညွှန်းပြီး အောက်တွင်ဖော်ပြထားသည့်အတိုင်း U 1 နှင့် U 2 ၏သေးငယ်ကြောင်း သတိရပါ။
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
n 1 နှင့် n 2 သည် နမူနာအရွယ်အစား 1 နှင့် 2 အသီးသီးဖြစ်ပြီး R 1 နှင့် R 2 တို့သည် နမူနာ 1 နှင့် 2 အတွက် အဆင့်များ၏ ပေါင်းလဒ်ဖြစ်သည်။
R 1 နှင့် R 2 ကိုရှာဖွေရန်အတွက် အုပ်စု နှစ်ခု လုံးမှ မှတ်သားချက်များကို ပေါင်းစပ်ပြီး ၎င်းတို့ကို အသေးငယ်ဆုံးမှ အကြီးဆုံးသို့ စီရန် လိုအပ်သည်-
| ဆေးအသစ် | PLACEBO |
|---|---|
| ၃ | ၄ |
| ၅ | ၈ |
| ၁ | ၆ |
| ၄ | ၂ |
| ၃ | ၁ |
| ၅ | ၉ |
စုစုပေါင်းနမူနာ- 1 ၊ 1 ၊ 2 ၊ 3 ၊ 3 ၊ 4 ၊ 4 ၊ 5 ၊ 5 ၊ 6 ၊ 8 ၊ 9
အဆင့်များ- 1.5 ၊ 1.5 ၊ 3 ၊ 4.5 ၊ 4.5 ၊ 6.5 ၊ 6.5 ၊ 8.5 ၊ 8.5 ၊ 10 ၊ 11 ၊ 12
R 1 = နမူနာ 1 အတွက် အဆင့်ပေါင်း = 1.5+4.5+4.5+6.5+8.5+8.5 = 34
R 2 = နမူနာ 2 အတွက် အဆင့်ပေါင်း = 1.5+3+6.5+10+11+12 = 44
ထို့နောက် ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏နမူနာအရွယ်အစား n 1 နှင့် n 2 အပြင် U 1 နှင့် U 2 ကိုရှာဖွေရန် ကျွန်ုပ်တို့၏အဆင့်ပေါင်း R 1 နှင့် R 2 ကိုအသုံးပြုသည်။
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
ကျွန်ုပ်တို့၏စမ်းသပ်မှုစာရင်းဇယားများသည် U1 နှင့် U2 ၏သေးငယ်သည်၊ ၎င်းမှာ U=13 ဖြစ်သည်။
မှတ်ချက်- U = 13 ကို ဆုံးဖြတ်ရန် Mann-Whitney U စမ်းသပ်ဂဏန်းတွက်စက် ကိုလည်း အသုံးပြုနိုင်သည်။
4. null hypothesis ကို ငြင်းပယ်ခြင်း သို့မဟုတ် ငြင်းပယ်ခြင်းမပြုပါနှင့်။
n 1 = 6 နှင့် n 2 = 6 ကို အရေးပါသည့်အဆင့် 0.05 ဖြင့်အသုံးပြု၍ Mann-Whitney U ဇယားက အရေးကြီးသောတန်ဖိုးမှာ 5 ဖြစ်သည်-
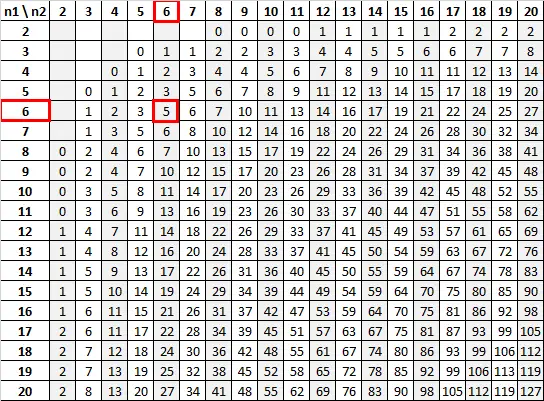
ကျွန်ုပ်တို့၏စမ်းသပ်စာရင်းအင်း (13) သည် ကျွန်ုပ်တို့၏အရေးကြီးသောတန်ဖိုး (5) ထက်ကြီးသောကြောင့်၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်ရန်ပျက်ကွက်ပါသည်။
5. ရလဒ်များကို ဘာသာပြန်ပါ။
ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းဆိုရန် ပျက်ကွက်ခဲ့သောကြောင့်၊ placebo အုပ်စုရှိ လူနာများခံစားရသော ထိတ်လန့်တိုက်ခိုက်မှုအရေအတွက်သည် ဆေးဝါးအုပ်စုအသစ်တွင် ကွဲပြားသည်ဟုဆိုရန် လုံလောက်သော အထောက်အထားမရှိပါ။
ဥပမာ ၂
တစ်ပတ်လျှင် မိနစ် 30 လေ့လာခြင်းသည် ကျောင်းသားများအား စာမေးပွဲတစ်ခုတွင် ပိုမိုကောင်းမွန်စွာလုပ်ဆောင်နိုင်စေမည်ကို ကျွန်ုပ်တို့သိချင်ပါသည်။ စုစုပေါင်းလူနာ 15 ဦးကို ကျပန်းလေ့လာရန် သို့မဟုတ် လေ့လာမှုအဖွဲ့မရှိပါ ။ တစ်ပတ်အကြာတွင် ကျောင်းသားအားလုံး တူညီသော စာမေးပွဲကို ဖြေကြသည်။
အုပ်စုနှစ်ခုလုံးအတွက် စမ်းသပ်မှုရလဒ်များကို အောက်တွင်ဖော်ပြထားသည်-
| လေ့လာချက် | လေ့လာမှုမရှိပါ။ |
|---|---|
| ၈၉ | ၈၈ |
| ၉၂ | ၉၃ |
| ၉၄ | ၉၅ |
| ၉၆ | ၇၅ |
| ၉၁ | ၇၂ |
| ၉၉ | ၈၀ |
| ၈၄ | ၈၁ |
| ၉၀ |
Mann-Whitney U စစ်ဆေးမှုကို လေ့လာမှုအုပ်စုအတွက် လေ့လာမှုမရှိသောအဖွဲ့နှင့် နှိုင်းယှဉ်ပါက စာမေးပွဲရမှတ်များ ကွာခြားမှုရှိမရှိကို ကြည့်ရှုပါ။ သိသာထင်ရှားမှုအဆင့် 0.01 ကိုသုံးပါ။
1. ယူဆချက်များကို ဖော်ပြပါ။
H 0 : လူဦးရေ နှစ်ခုသည် ညီမျှသည်။
H a : လူဦးရေနှစ်ခုက မညီဘူး။
2. ယူဆချက်အတွက် အသုံးပြုရန် အရေးပါမှုအဆင့်ကို သတ်မှတ်ပါ။
ပြဿနာက ကျွန်ုပ်တို့သည် 0.01 ၏ အရေးပါမှုအဆင့်ကို အသုံးပြုသင့်သည်ဟု ဆိုသည်။
3. စမ်းသပ်စာရင်းအင်းကိုရှာပါ။
စမ်းသပ်စာရင်းအင်းသည် U ကိုရည်ညွှန်းပြီး အောက်တွင်ဖော်ပြထားသည့်အတိုင်း U 1 နှင့် U 2 ၏သေးငယ်ကြောင်း သတိရပါ။
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
n 1 နှင့် n 2 သည် နမူနာအရွယ်အစား 1 နှင့် 2 အသီးသီးဖြစ်ပြီး R 1 နှင့် R 2 တို့သည် နမူနာ 1 နှင့် 2 အတွက် အဆင့်များ၏ ပေါင်းလဒ်ဖြစ်သည်။
R 1 နှင့် R 2 ကိုရှာဖွေရန်အတွက် အုပ်စု နှစ်ခု လုံးမှ မှတ်သားချက်များကို ပေါင်းစပ်ပြီး ၎င်းတို့ကို အသေးငယ်ဆုံးမှ အကြီးဆုံးသို့ စီရန် လိုအပ်သည်-
| လေ့လာချက် | လေ့လာမှုမရှိပါ။ |
|---|---|
| ၈၉ | ၈၈ |
| ၉၂ | ၉၃ |
| ၉၄ | ၉၅ |
| ၉၆ | ၇၅ |
| ၉၁ | ၇၂ |
| ၉၉ | ၈၀ |
| ၈၄ | ၈၁ |
| ၉၀ |
စုစုပေါင်းနမူနာ- 72 , 75 , 80 , 81 , 84 , 88 , 89 , 90 , 91 , 92 , 93 , 94 , 95 , 96 , 99
အတန်းများ- 1 ၊ 2 ၊ 3 ၊ 4 ၊ 5 ၊ 6 ၊ 7 ၊ 8 ၊ 9 ၊ 10 ၊ 11 ၊ 12 ၊ 13 ၊ 14 ၊ 15
R 1 = နမူနာ 1 အတွက် အဆင့်ပေါင်း = 5+7+8+9+10+12+14+15 = 80
R 2 = နမူနာ 2 အတွက် အဆင့်ပေါင်း = 1+2+3+4+6+11+13 = 40
ထို့နောက် ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏နမူနာအရွယ်အစား n 1 နှင့် n 2 အပြင် U 1 နှင့် U 2 ကိုရှာဖွေရန် ကျွန်ုပ်တို့၏အဆင့်ပေါင်း R 1 နှင့် R 2 ကိုအသုံးပြုသည်။
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
ကျွန်ုပ်တို့၏စမ်းသပ်မှုစာရင်းဇယားများသည် U1 နှင့် U2 ၏သေးငယ်သည်၊ ၎င်းမှာ U=12 ဖြစ်သည်။
မှတ်ချက်- U = 12 ကို ဆုံးဖြတ်ရန် Mann-Whitney U စမ်းသပ်ဂဏန်းတွက်စက် ကိုလည်း အသုံးပြုနိုင်သည်။
4. null hypothesis ကို ငြင်းပယ်ခြင်း သို့မဟုတ် ငြင်းပယ်ခြင်းမပြုပါနှင့်။
n 1 = 8 နှင့် n 2 = 7 ကို 0.01 ၏ အရေးပါသောအဆင့်ဖြင့် အသုံးပြု၍ Mann-Whitney U ဇယားက အရေးကြီးသောတန်ဖိုးမှာ 6 ဖြစ်သည်-
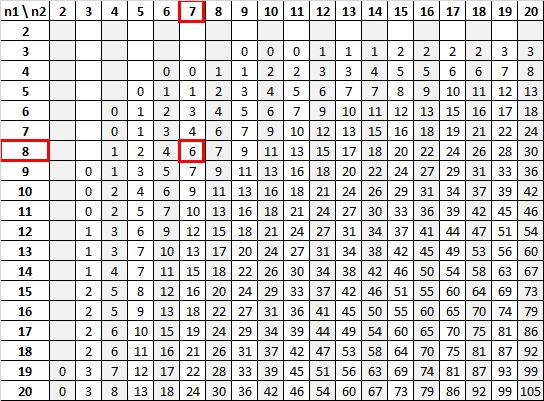
ကျွန်ုပ်တို့၏စမ်းသပ်စာရင်းအင်း (12) သည် ကျွန်ုပ်တို့၏အရေးကြီးသောတန်ဖိုး (6) ထက်ကြီးသောကြောင့်၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်ရန်ပျက်ကွက်ပါသည်။
5. ရလဒ်များကို ဘာသာပြန်ပါ။
null hypothesis ကို ငြင်းဆိုရန် ပျက်ကွက်ခဲ့သဖြင့် လေ့လာခဲ့သော ကျောင်းသားများ၏ စာမေးပွဲရမှတ်များသည် စာမကျက်သော ကျောင်းသားများနှင့် ကွဲပြားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထား မရှိပါ။
ထပ်လောင်းအရင်းအမြစ်များ
Mann-Whitney U စမ်းသပ်ဂဏန်းပေါင်းစက်
Mann-Whitney U Table
Excel တွင် Mann-Whitney U Test ကိုမည်သို့လုပ်ဆောင်ရမည်နည်း။
R တွင် Mann-Whitney U စမ်းသပ်မှုပြုလုပ်နည်း
Python တွင် Mann-Whitney U Test ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
SPSS တွင် Mann-Whitney U Test ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
Stata ရှိ Mann-Whitney U စမ်းသပ်မှုပြုလုပ်နည်း
စာရေးသူအကြောင်း
Benjamin Anderson
မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။