ပြီးပြည့်စုံသောလမ်းညွှန်- manova ယူဆချက်များကို စစ်ဆေးနည်း

တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကိန်းရှင်များသည် တုံ့ပြန်မှုကိန်းရှင်များစွာကို မည်ကဲ့သို့ အကျိုးသက်ရောက်သည်ကို ခွဲခြမ်းစိတ်ဖြာရန် MANOVA (မူကွဲကွဲပြားမှုအမျိုးမျိုးကို ခွဲခြမ်းစိတ်ဖြာခြင်း) ကို အသုံးပြုသည်။

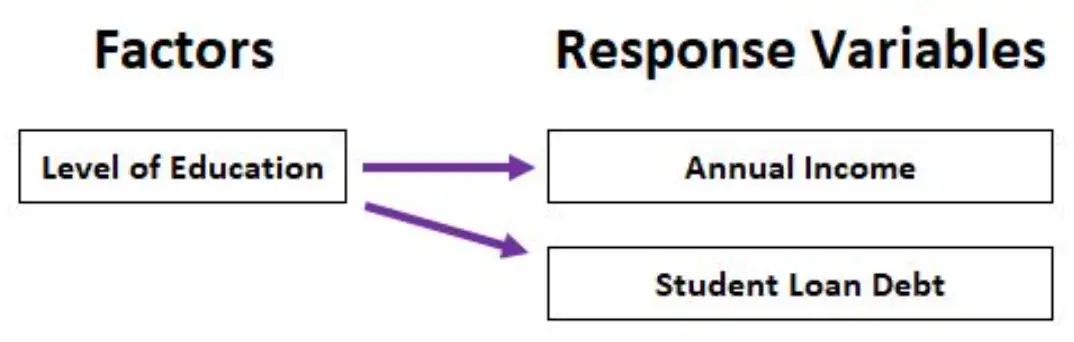
ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် ပညာရေးအဆင့် (အထက်တန်းဒီပလိုမာ၊ တွဲဘက်ဘွဲ့၊ ဘွဲ့၊ မဟာဘွဲ့) သည် နှစ်စဉ်ဝင်ငွေနှင့် ကျောင်းသားချေးငွေ စုစုပေါင်းကြွေးမြီအပေါ် မည်ကဲ့သို့ အကျိုးသက်ရောက်သည်ကို ခွဲခြမ်းစိတ်ဖြာရန် MANOVA ကို အသုံးပြုနိုင်သည်။

ဆက်စပ်- ANOVA၊ ANCOVA၊ MANOVA နှင့် MANCOVA အကြား ကွာခြားချက်များ

ကျွန်ုပ်တို့ MANOVA ကို လုပ်ဆောင်သည့်အခါတိုင်း၊ အောက်ပါ ယူဆချက်များနှင့် ကိုက်ညီကြောင်း စစ်ဆေးရပါမည်။

1. Multivariate normality – တုံ့ပြန်မှု variable များသည် factor variable(များ) အုပ်စုတစ်ခုစီအတွင်း ပုံမှန်အားဖြင့် multivariate ဖြန့်ဝေပါသည်။

2. လွတ်လပ်ရေး – ရှုမြင်မှုတစ်ခုစီကို လူဦးရေထံမှ ကျပန်းနှင့် အမှီအခိုကင်းစွာ နမူနာယူထားသည်။

3. တူညီသောကွဲလွဲမှု – အုပ်စုတစ်ခုစီ၏ လူဦးရေကွာဟချက်မာထရစ်များသည် တူညီသည်။

4. Multivariate outliers မရှိပါ – လွန်ကဲသော multivariate outliers မရှိပါ။

ဤဆောင်းပါးတွင်၊ ကျွန်ုပ်တို့သည် ယူဆချက်တစ်ခုစီ၏ ရှင်းလင်းချက်အပြင် ယူဆချက်နှင့်ကိုက်ညီခြင်းရှိမရှိကို မည်သို့ဆုံးဖြတ်ရမည်နည်း။

ယူဆချက် 1- ပုံမှန်ပုံစံမျိုးစုံ

MANOVA သည် တုံ့ပြန်မှုကိန်းရှင်များကို ကိန်းရှင်ကိန်းရှင်အုပ်စုတစ်ခုစီအတွင်း ပုံမှန်အားဖြင့် ကွဲပြားစွာဖြန့်ဝေသည်ဟု ယူဆသည်။

အချက်တစ်ခုစီအတွက် လေ့လာတွေ့ရှိချက် အနည်းဆုံး 20 ခုရှိလျှင် * တုံ့ပြန်မှုမပြောင်းလဲနိုင်သော ပေါင်းစပ်မှု ပေါင်းစပ်မှု အမျိုးမျိုးကွဲပြားမှု ပုံမှန်ဖြစ်ခြင်း၏ ယူဆချက်နှင့် ကိုက်ညီသည်ဟု ကျွန်ုပ်တို့ ယူဆနိုင်ပါသည်။

အချက်တစ်ခုစီအတွက် ရှုမြင်မှု 20 ထက်နည်းသော တုံ့ပြန်မှုမပြောင်းလဲနိုင်သောပေါင်းစပ်မှုရှိပါက၊ ကျန်ရှိသည့်အရာများကို မြင်သာစေရန်နှင့် ဤယူဆချက်နှင့်ကိုက်ညီမှုရှိမရှိ အမြင်ဖြင့်စစ်ဆေးရန် scatterplot matrix ကိုဖန်တီးနိုင်ပါသည်။

ကံကောင်းထောက်မစွာ၊ MANOVA သည် အမျိုးမျိုးကွဲပြားသော ပုံမှန်ပုံစံမှ သွေဖည်သွားစေရန် ခိုင်ခံ့ကြောင်း ကောင်းစွာသိထားသောကြောင့် အသေးစားမှ အလယ်အလတ်သွေဖည်မှုများသည် ယေဘုယျအားဖြင့် ပြဿနာမဟုတ်ပါ။

အယူအဆ ၂- လွတ်လပ်ရေး

MANOVA သည် စောင့်ကြည့်မှုတစ်ခုစီကို လူဦးရေထံမှ ကျပန်းနှင့် သီးခြားနမူနာယူသည်ဟု ယူဆသည်။

ဖြစ်နိုင်ခြေနမူနာနည်းလမ်း (လူဦးရေတစ်ခုစီတွင် နမူနာအဖြစ်ရွေးချယ်ခံရရန် တူညီသောဖြစ်နိုင်ခြေရှိသည်) ဒေတာစုဆောင်းရန်အတွက် အသုံးပြုထားသရွေ့ လေ့လာဆန်းစစ်မှုတစ်ခုစီကို ကျပန်းနှင့် အမှီအခိုကင်းသောပုံစံဖြင့် နမူနာယူထားသည်ဟု ကျွန်ုပ်တို့ ယူဆနိုင်ပါသည်။

ဖြစ်နိုင်ခြေနမူနာနည်းလမ်းများ ဥပမာများ ပါဝင်သည်-

• ရိုးရှင်းသော ကြမ်ဖက်မှု
• အချိုးကျနမူနာပြခြင်း။
• ကျပန်းအစုလိုက် နမူနာယူခြင်း။
• စနစ်ကျနမူနာ

ယူဆချက် 3- တန်းတူကွဲလွဲမှု

MANOVA သည် အုပ်စုတစ်ခုစီ၏ လူဦးရေ ကွာဟမှု မက်ထရစ်များ ညီမျှသည်ဟု ယူဆသည်။

ဤယူဆချက်ကို စမ်းသပ်ရန် အသုံးအများဆုံးနည်းလမ်းမှာ Box’s M test ကို အသုံးပြုခြင်းဖြစ်သည်။ ဤစစ်ဆေးမှုသည် အတော်လေး တင်းကျပ်သည်ဟု သိရှိရသောကြောင့်၊ ထို့ကြောင့် ကျွန်ုပ်တို့သည် ယေဘုယျအားဖြင့် လူဦးရေ ကွာဟမှုမက်ထရစ်များကို တူညီမှုရှိမရှိ ဆုံးဖြတ်ရန် ယေဘုယျအားဖြင့် 0.001 ကို အသုံးပြုပါသည်။

Box’s M test ၏ p-value သည် 0.001 ထက် ကြီးပါက၊ ဤယူဆချက်နှင့် ကိုက်ညီသည်ဟု ကျွန်ုပ်တို့ ယူဆနိုင်ပါသည်။

ကံအားလျော်စွာ၊ စမ်းသပ်မှု၏ p-value သည် 0.001 ထက်နည်းသော်လည်း၊ MANOVA သည် ဤယူဆချက်မှ သွေဖည်ရန် ခိုင်ခံ့နေတတ်သည်။

ညီမျှခြင်းမဟုတ်သော မက်ထရစ်များကို ပြဿနာဖြစ်စေရန်အတွက်၊ ကွဲလွဲမှုမက်ထရစ်များအကြား ခြားနားချက်များသည် အလွန်ပြင်းထန်ရပါမည်။

Hypothesis 4- ကွဲပြားသော အကြမ်းဖျင်း ကွဲပြားမှုများ မရှိပါ။

ရလဒ်များကို သိသိသာသာ လွှမ်းမိုးနိုင်သည့် ဒေတာတွင် လွန်ကဲကွဲပြားသော အစွန်းအထင်းများ မရှိဟု MANOVA က ယူဆသည်။

ဤယူဆချက်ကို အတည်ပြုရန် အသုံးအများဆုံးနည်းလမ်းမှာ ရှုခင်းတစ်ခုစီအတွက် Mahalanobis အကွာအဝေးကို တွက်ချက်ရန်ဖြစ်ပြီး၊ မျိုးစုံကွဲပြားသော နေရာတစ်ခုရှိ အမှတ်နှစ်ခုကြားအကွာအဝေးကို ကိုယ်စားပြုသည့် အကွာအဝေးကို ကိုယ်စားပြုသည်။

အကယ်၍ စောင့်ကြည့်မှုတစ်ခု၏ Mahalanobis အကွာအဝေးအတွက် သက်ဆိုင်သော p-တန်ဖိုးသည် 0.001 ထက်နည်းပါက၊ ကျွန်ုပ်တို့သည် အဆိုပါရှုမြင်မှုကို လွန်ကဲသောအစွန်းထွက်တစ်ခုအဖြစ် ယေဘုယျအားဖြင့် ကြေညာသည်။

စာရင်းအင်းဆော့ဖ်ဝဲအမျိုးမျိုးတွင် Mahalanobis အကွာအဝေးကို တွက်ချက်နည်းကို ကြည့်ရှုရန် အောက်ပါသင်ခန်းစာများကို ကိုးကားပါ။

• R တွင် Mahalanobis အကွာအဝေးကို မည်ကဲ့သို့တွက်ရမည်နည်း။
• SPSS တွင် Mahalanobis အကွာအဝေးကိုမည်သို့တွက်ချက်နည်း
• Python ရှိ Mahalanobis အကွာအဝေးကို တွက်နည်း

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများတွင် MANOVA တစ်ခုအား စာရင်းအင်းဆော့ဖ်ဝဲအမျိုးမျိုးတွင် မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

R ဖြင့် MANOVA ကိုမည်သို့လုပ်ဆောင်ရမည်နည်း။
SPSS တွင် MANOVA မည်ကဲ့သို့လုပ်ဆောင်ရမည်နည်း။
Stata တွင် MANOVA ကိုမည်သို့လုပ်ဆောင်ရမည်နည်း။