Marginal ပျမ်းမျှဆိုတာဘာလဲ။ (အဓိပ္ပါယ် & #038; ဥပမာ)

အရေးပေါ်ဇယားတစ်ခုတွင်၊ ကိန်းရှင်တစ်ခု၏ marginal means များသည် အခြားသော variable အဆင့်တစ်ခုစီတွင်ရှိသော ထိုကိန်းရှင်၏ ပျမ်းမျှနည်းလမ်းများဖြစ်သည်။

၎င်းတို့၏အမည်ဖော်ပြသည့်အတိုင်း၊ ဤပျမ်းမျှကိန်းဂဏန်းများသည် အရေးပေါ်အခြေအနေဇယား၏ အနားသတ် များတွင် ပေါ်နေပါသည်။

အောက်ဖော်ပြပါ ဥပမာသည် ပေးထားသော အရေးပေါ်ဇယားအတွက် မဖြစ်စလောက် အဓိပ္ပါယ်များကို တွက်ချက်နည်းကို ပြသထားသည်။

ဥပမာ- marginal averages တွက်ချက်ခြင်း။

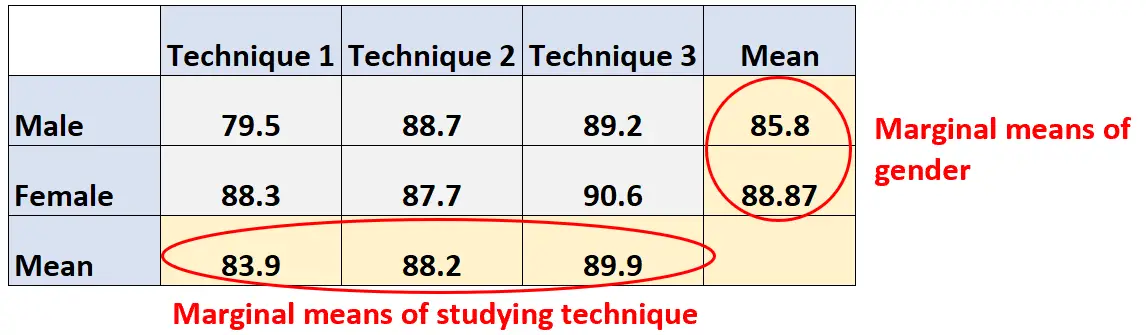
အောက်ဖော်ပြပါ အရေးပေါ်ဇယားတွင် စာမေးပွဲအတွက် ပြင်ဆင်ရန် မတူညီသော လေ့လာမှုနည်းပညာသုံးမျိုးကို အသုံးပြုခဲ့သည့် ကျောင်းသား 100 ၏ ပျမ်းမျှ စာမေးပွဲရမှတ်ကို ပြသထားသည်။

အတန်းများသည် ကျောင်းသား၏ လိင်အမျိုးအစားကိုပြသပြီး ကော်လံများတွင် ၎င်းတို့အသုံးပြုသော လေ့လာမှုနည်းပညာကို ပြသသည်-

gender marginal ဆိုသည်မှာ သင်ကြားရေးနည်းပညာအဆင့်တစ်ခုစီအတွက် ပျမ်းမျှအားဖြင့် ကျားမအဆင့်တစ်ခုစီ၏ ဆိုလိုရင်းဖြစ်သည်။

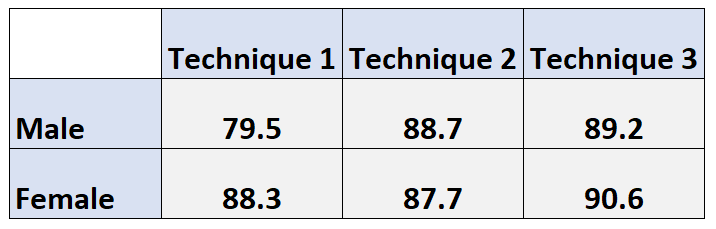
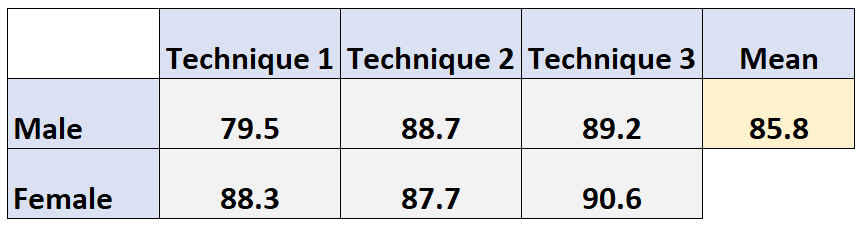
ဥပမာအားဖြင့်၊ အမျိုးသားများအတွက် ပျမ်းမျှမဖြစ်စလောက်စာမေးပွဲရမှတ်ကို အောက်ပါအတိုင်း တွက်ချက်ပါသည်။

အမျိုးသားများအတွက် မဖြစ်စလောက် ပျမ်းမျှ- (79.5 + 88.7 + 89.2) / 3 = 85.8

အလားတူ၊ အမျိုးသမီးများအတွက် မဖြစ်စလောက် ပျမ်းမျှ စာမေးပွဲရမှတ်ကို အောက်ပါအတိုင်း တွက်ချက်ပါသည်။

အမျိုးသမီးများအတွက် မဖြစ်စလောက် ပျမ်းမျှ- (88.3 + 87.7 + 90.6) / 3 = 88.87

လေ့လာရေးနည်းစနစ်၏ မဖြစ်စလောက်နည်းလမ်းများ သည် ကျားမအဆင့်တစ်ခုစီအတွက် ပျမ်းမျှအားဖြင့် လေ့လာမှုအဆင့်တစ်ခုစီ၏ နည်းလမ်းများဖြစ်သည်။

ဥပမာအားဖြင့်၊ နည်းပညာ 1 ကိုအသုံးပြုသော ကျောင်းသားများ၏ မဖြစ်စလောက် ပျမ်းမျှ စာမေးပွဲရမှတ်ကို အောက်ပါအတိုင်း တွက်ချက်သည်-

နည်းလမ်း၏မဖြစ်စလောက်ပျမ်းမျှ 1- (79.5 + 88.3) / 2 = 83.9

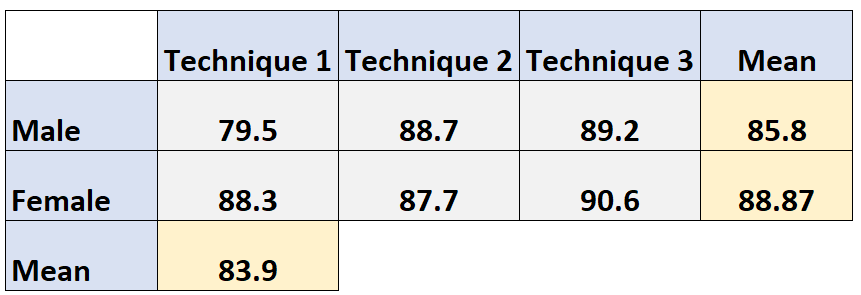
နည်းပညာ 2 ကိုအသုံးပြုသော ကျောင်းသားများ၏ မဖြစ်စလောက် ပျမ်းမျှ စာမေးပွဲရမှတ်ကို အောက်ပါအတိုင်း တွက်ချက်ပါသည်။

Marginal average of technique 2: (88.7 + 87.7) / 2 = 88.2

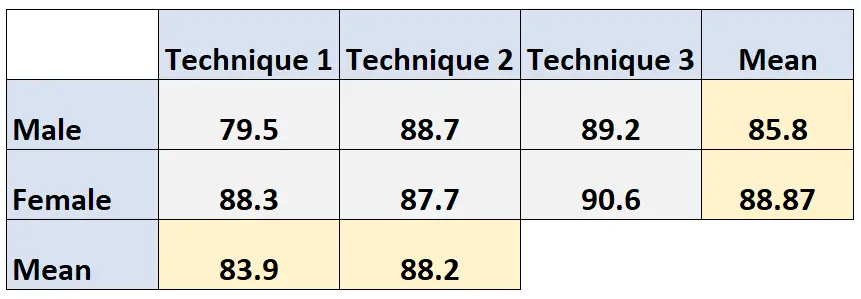
နည်းပညာ 3 ကိုအသုံးပြုသောကျောင်းသားများ၏မဖြစ်စလောက်ပျမ်းမျှစာမေးပွဲရမှတ်ကိုအောက်ပါအတိုင်းတွက်ချက်သည်-

နည်းစနစ်၏ မဖြစ်စလောက် ပျမ်းမျှ 3- (89.2 + 90.6) / 2 = 89.9

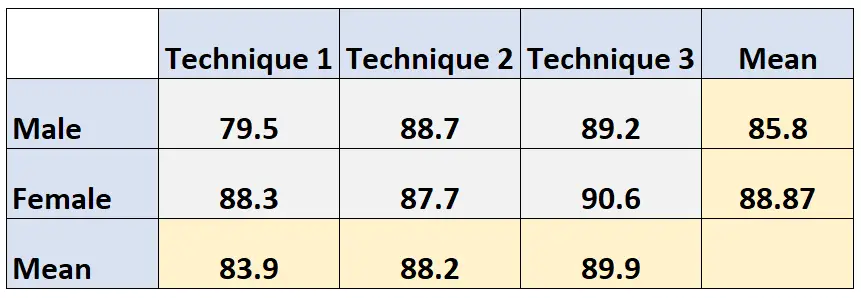
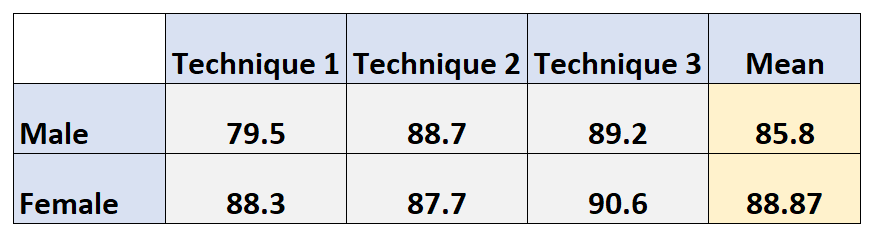
ကိန်းရှင်နှစ်ခု၏ မဖြစ်စလောက်ဆိုလိုသည်မှာ အရေးပေါ်ဇယား၏ အနားသတ် များတွင် ပေါ်လာသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်-

အဘယ်ကြောင့် မဖြစ်စလောက်ကို မှီခိုနေရသနည်း ။

Marginal ဆိုသည်မှာ ကိန်းရှင်အဆင့်တစ်ခုအတွက် ပျမ်းမျှတန်ဖိုးကို ပြောပြသောကြောင့် ၎င်းတို့သည် အသုံးဝင်ပါသည်။

ဥပမာအားဖြင့်၊ ယခင်အခြေအနေတွင်၊ ကျွန်ုပ်တို့သည် အောက်ပါတို့ကို သိထားသည်-

• လေ့လာမှုနည်းလမ်း 1 ကိုအသုံးပြုသော အမျိုးသားများအတွက် ပျမ်းမျှစာမေးပွဲရမှတ်မှာ 79.5 ဖြစ်သည်။
• လေ့လာမှုနည်းပညာ 2 ကိုအသုံးပြုသော အမျိုးသားများအတွက် ပျမ်းမျှစာမေးပွဲရမှတ်မှာ 88.7 ဖြစ်သည်။
• လေ့လာမှုနည်းလမ်း 3 ကိုအသုံးပြုသော အမျိုးသားများအတွက် ပျမ်းမျှစာမေးပွဲရမှတ်မှာ 89.2 ဖြစ်သည်။

ဒါပေမယ့် အမျိုးသားတွေရဲ့ ပျမ်းမျှရမှတ်ကို သိချင်ရင်ကော။

အမျိုးသားများအတွက် အနည်းအကျဉ်းပျမ်းမျှသည် ဤအရာကိုဖြေဆိုနိုင်သည်- အမျိုးသားများအတွက် စုစုပေါင်းပျမ်းမျှရမှတ်မှာ 85.8 ဖြစ်သည်။

အလားတူပင်၊ ကျွန်ုပ်တို့သည် အောက်ပါတို့ကို သိခဲ့ကြသည်-

• လေ့လာမှုနည်းလမ်း 1 ကိုအသုံးပြုသော အမျိုးသားများအတွက် ပျမ်းမျှစာမေးပွဲရမှတ်မှာ 79.5 ဖြစ်သည်။
• လေ့လာမှုနည်းလမ်း 1 ကိုအသုံးပြုသော အမျိုးသမီးများအတွက် ပျမ်းမျှစာမေးပွဲရမှတ်မှာ 88.3 ဖြစ်သည်။

ဒါပေမယ့် လေ့လာမှုနည်းပညာ 1 ကိုအသုံးပြုတဲ့ ကျောင်းသားတွေရဲ့ စုစုပေါင်းပျမ်းမျှရမှတ်ကို သိချင်ရင်ကော။

လေ့လာမှုနည်းပညာအတွက် အနည်းအကျဉ်းပျမ်းမျှသည် ဤအရာကိုဖြေဆိုနိုင်သည်- လေ့လာမှုနည်းစနစ် 1 ကိုအသုံးပြုသော ကျောင်းသားများ၏ စုစုပေါင်းပျမ်းမျှရမှတ်မှာ 83.9 ဖြစ်သည်။

အခြေခံအားဖြင့်၊ marginal averages များသည် သီးခြားကိန်းရှင်အဆင့်များအတွက် ပျမ်းမျှများကို နားလည်ရန် ရိုးရှင်းသောနည်းလမ်းကိုပေးပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

မဖြစ်စလောက် ဖြန့်ဖြူးခြင်းဆိုသည်မှာ အဘယ်နည်း။
ပူးတွဲဖြန့်ဝေခြင်းဆိုသည်မှာ အဘယ်နည်း။
အခြေအနေအရ ဖြန့်ဖြူးခြင်းဆိုသည်မှာ အဘယ်နည်း။