Stata တွင် mcnemar စမ်းသပ်မှုပြုလုပ်နည်း
McNemar စမ်းသပ်မှု သည် တွဲထားသောဒေတာများကြားတွင် ကိန်းဂဏန်းဆိုင်ရာ သိသာထင်ရှားသော အချိုးအစားများ ရှိမရှိ ဆုံးဖြတ်ရန် ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည့် စမ်းသပ်မှုတစ်ခုဖြစ်သည်။
ဤသင်ခန်းစာသည် Stata ရှိ McNemar စမ်းသပ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။
ဥပမာ- Stata တွင် McNemar စမ်းသပ်မှု
အချို့သော စျေးကွက်ရှာဖွေရေး ဗီဒီယိုတစ်ခုသည် ဥပဒေတစ်ခုအပေါ် လူများ၏ ထင်မြင်ယူဆချက်များကို ပြောင်းလဲနိုင်မလားဟု သုတေသီများ သိချင်သည်ဆိုကြပါစို့။ ၎င်းတို့သည် ဥပဒေကို ထောက်ခံခြင်း ရှိ၊ မရှိ သိရှိရန် လူ 100 ကို စစ်တမ်းကောက်ယူခဲ့သည်။ ထို့နောက် ၎င်းတို့သည် လူ 100 တို့အား စျေးကွက်ရှာဖွေရေး ဗီဒီယိုကို ပြသပြီး ဗီဒီယိုပြီးဆုံးပြီးနောက် ၎င်းတို့ကို ထပ်မံ စစ်တမ်းကောက်ယူသည်။
အောက်ဖော်ပြပါဇယားသည် ဗီဒီယိုကိုမကြည့်မီနှင့် အပြီးတွင် ဥပဒေအား ထောက်ခံသူ စုစုပေါင်းအရေအတွက်ကို ပြသသည်-
| စျေးကွက်ရှာဖွေရေးမတိုင်မီဗီဒီယို | ||
|---|---|---|
| စျေးကွက်ရှာဖွေရေးပြီးနောက်ဗီဒီယို | အထောက်အပံ့ | မနေနိုင် |
| အထောက်အပံ့ | ၃၀ | ၄၀ |
| မနေနိုင် | ၁၂ | ၁၈ |
ဗီဒီယိုကိုမကြည့်မီနှင့် ဗီဒီယိုကြည့်ရှုပြီးနောက် ဥပဒေထောက်ခံသူအချိုးတွင် ကိန်းဂဏန်းသိသိသာသာ ကွာခြားမှုရှိမရှိ ဆုံးဖြတ်ရန်၊ ကျွန်ုပ်တို့သည် McNemar စမ်းသပ်မှုကို လုပ်ဆောင်နိုင်သည်။
Stata တွင်၊ McNemar စမ်းသပ်မှုကို လုပ်ဆောင်ရန် mcci အမိန့်ကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည်။ ကျွန်ုပ်တို့သည် 2×2 ဇယားကို ဘယ်မှညာ၊ အပေါ်မှအောက်ခြေသို့ ထည့်သည်-
McCi 30 40 12 ၁၈
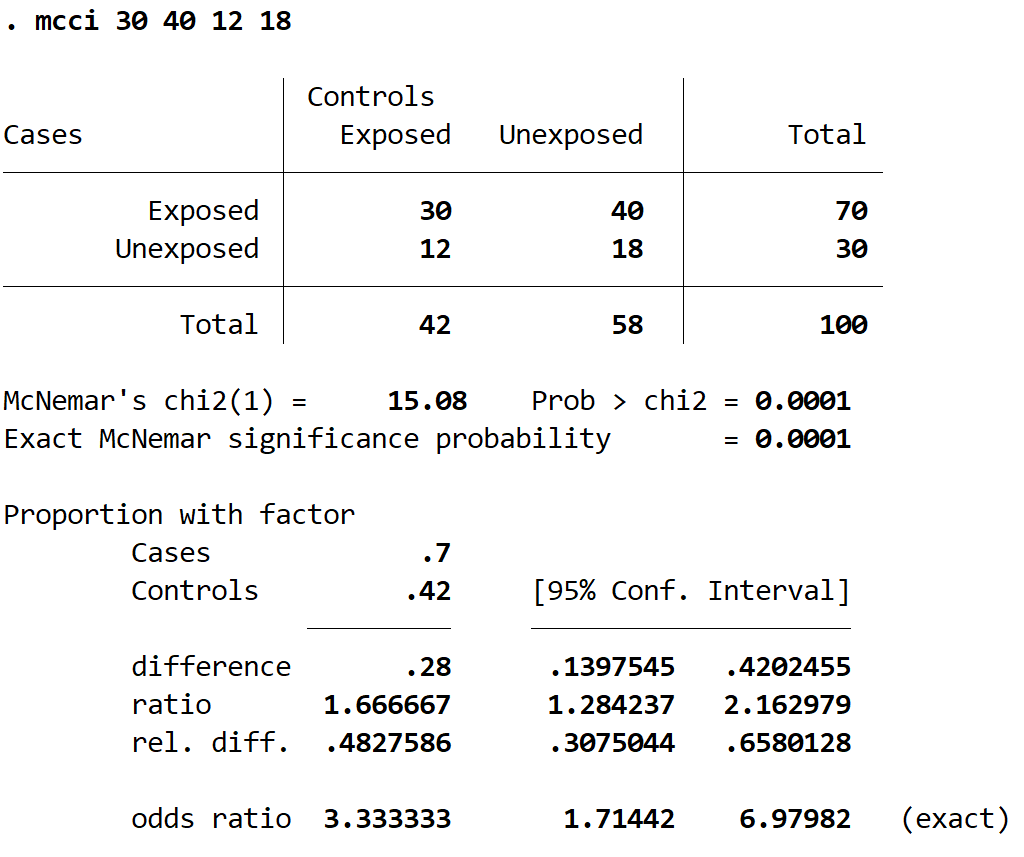
ဤသည်မှာ ရလဒ်ကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-
2 × 2 ဇယား- Stata သည် case-control လေ့လာမှုများတွင် တွေ့ရလေ့ရှိသော သမားရိုးကျ အညွှန်းများကို အသုံးပြု၍ 2×2 အရေအတွက်ဇယားကို ပြသသည်။ စုစုပေါင်းအကောင့် 100 အထိ ပေါင်းထားသည်ကို ကျွန်ုပ်တို့တွေ့နိုင်သည်။
McNemar’s Chi2(1)- ဤသည်မှာ 15.08 ဖြစ်သည့် chi-square စမ်းသပ်မှု ကိန်းဂဏန်းဖြစ်သည်။ Stata သည် ဤတန်ဖိုးကိုတွက်ချက်ရန် အောက်ပါဖော်မြူလာကိုအသုံးပြုသည်- (40-12) 2 / (40+12) = 784 / 52 = 15.0769။
Prob > chi2- ဤသည်မှာ chi-square စမ်းသပ်မှု ကိန်းဂဏန်းနှင့် ဆက်စပ်နေသည့် p-value ဖြစ်သည်။ 0.0001 ဖြစ်သွားပါတယ်။ ဤတန်ဖိုးသည် 0.05 ထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့သည် null အယူအဆကို ငြင်းပယ်နိုင်ပြီး စျေးကွက်ရှာဖွေရေးဗီဒီယိုကိုမကြည့်မီနှင့် ပြီးနောက် ဥပဒေကို ထောက်ခံသူအချိုးအစားမှာ ကိန်းဂဏန်းအရ သိသာထင်ရှားစွာ ကွာခြားသည်ဟု ကောက်ချက်ချနိုင်သည်။
ချီစတုရန်းတွက်ချက်မှုမှတ်စု
အောက်ပါ 2×2 ဇယားကိုပေးသည်-
| စျေးကွက်ရှာဖွေရေးမတိုင်မီဗီဒီယို | ||
|---|---|---|
| စျေးကွက်ရှာဖွေရေးပြီးနောက်ဗီဒီယို | အထောက်အပံ့ | မနေနိုင် |
| အထောက်အပံ့ | ရှိသည် | ခ |
| မနေနိုင် | VS | ဃ |
Stata သည် Chi-square စမ်းသပ်မှုစာရင်းအင်းကိုတွက်ချက်ရန် ဖော်မြူလာ (BC) 2 / (B+C) ကိုအသုံးပြုသည်။
သို့သော်၊ အချို့သောစာရင်းအင်းဖတ်စာအုပ်များတွင် ဖော်မြူလာ (|BC| – 1) 2 / (B+C) ကို ဇယားရှိ ဂဏန်းများ သေးငယ်သောအခါ အဆက်ပြတ်ပြင်ဆင်မှုအဖြစ် အသုံးပြုရန် အကြံပြုထားသည်။ ပုံမှန်အားဖြင့်၊ ဆဲလ်အရေအတွက် 5 ထက်နည်းသောအခါတွင် ဤပြင်ဆင်မှုကို အများအားဖြင့် အသုံးပြုသည်။