Moran's self ဆိုတာဘာလဲ။ (အဓိပ္ပါယ် & #038; ဥပမာ)

Moran’s I သည် spatial autocorrelation ကိုတိုင်းတာသည့်နည်းလမ်းဖြစ်သည်။

ရိုးရိုးရှင်းရှင်းပြောရလျှင်၊ ၎င်းသည် 2D space တွင် တန်ဖိုးများ မည်မျှ နီးကပ်စွာ အစုလိုက်အပြုံလိုက် မည်မျှရှိသည်ကို တွက်ချက်ရန် နည်းလမ်းတစ်ခုဖြစ်သည်။ အိမ်ထောင်စုဝင်ငွေ၊ ပညာရေးအဆင့် စသည်တို့ကဲ့သို့ မြေပုံပေါ်တွင် မတူညီသောအင်္ဂါရပ်များကို အုပ်စုဖွဲ့ထားသည်ကို တိုင်းတာရန် ပထဝီဝင်နှင့် ပထဝီဝင်အချက်အလက်သိပ္ပံ (GIS) တွင် အသုံးပြုလေ့ရှိသည်။

Moran’s I: ဖော်မြူလာ

Moran’s I တွက်ချက်ရန် ဖော်မြူလာမှာ-

ငါ = (N/W)*ΣΣw _ij (x _i – x )(x _j – x )/Σ(x _i – x ) ²

ရွှေ-

• N- i နှင့် j ဖြင့် ညွှန်းထားသော spatial ယူနစ်အရေအတွက်
• W: w _ij အားလုံး၏ပေါင်းလဒ်
• x- အတိုးနှုန်းပြောင်းလဲခြင်း (အိမ်ထောင်စုဝင်ငွေ၊ ကျောင်းတက်သည့်နှစ်စသည်ဖြင့်)
• x : x ပျမ်းမျှ
• w _ij : spatial weights ၏ matrix တစ်ခု

စာရင်းအင်းဆော့ဖ်ဝဲလ်အများစုသည် ၎င်းကို သင့်အတွက် တွက်ချက်ပေးနိုင်သောကြောင့် ဤတိုင်းတာမှုကို သင်လက်ဖြင့် တွက်ချက်ရန် ဘယ်သောအခါမှ ဖြစ်ကောင်းဖြစ်နိုင်လိမ့်မည်မဟုတ်ပေ။

Moran’s I ၏တန်ဖိုးသည် -1 မှ 1 အထိရှိနိုင်သည်။

• -1- အတိုးနှုန်းပြောင်းလဲမှုသည် လုံးဝကွဲထွက်သွားသည်။
• 0- အကျိုးစီးပွားပြောင်းလဲမှုသည် ကျပန်းအားဖြင့် ကွဲပြားသည်။
• 1- အကျိုးစီးပွားပြောင်းလဲမှုကို စုံလင်စွာအုပ်စုဖွဲ့ထားသည်။

Moran’s I တွက်ချက်ခြင်းနှင့်အတူ၊ စာရင်းအင်းဆော့ဖ်ဝဲလ်အများစုသည် ဒေတာများ ကျပန်းကွဲသွားခြင်း ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုနိုင်သည့် သက်ဆိုင်ရာ p-value ကို တွက်ချက်ပါသည်။

Moran စမ်းသပ်မှုတွင် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြုသည် ။

Null hypothesis (H ₀ ) : ဒေတာများသည် ကျပန်း ကွဲသွားပါသည်။

Alternative hypothesis ( _HA ) : ဒေတာများကို ကျပန်းခွဲဝေခြင်း မဟုတ်ပါ ၊ ဆိုလိုသည်မှာ ၎င်းကို မြင်နိုင်သောပုံစံများဖြင့် အုပ်စုဖွဲ့ထားသည်။

Moran’s I နှင့် သက်ဆိုင်သော p-တန်ဖိုးသည် အချို့သော အရေးပါမှုအဆင့် (ဆိုလိုသည်မှာ α = 0.05) အောက်တွင် ရှိနေပါက၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းဆိုနိုင်ပြီး ၎င်းတို့သည် နေရာဒေသအလိုက် အစုလိုက်အပြုံလိုက် ဖြစ်ဖွယ်မရှိဟု ကောက်ချက်ချနိုင်သည်။ မတော်တဆဖြစ်သွားတယ်။

Moran’s I- ဥပမာအချို့

အောက်ပါဥပမာများသည် Moran’s I အတွက် မတူညီသောတန်ဖိုးများဖြင့် မှားယွင်းသောကတ်များကို ကိုယ်စားပြုပါသည်။

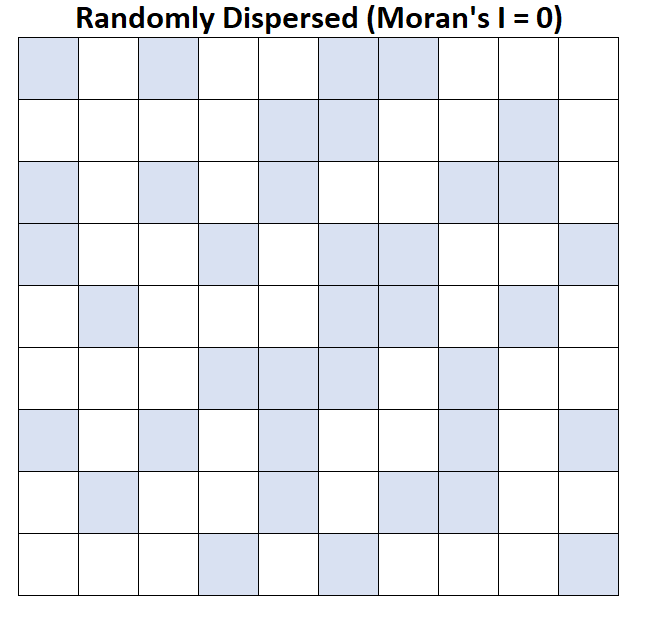
မြေပုံပေါ်ရှိ စတုရန်းတစ်ခုစီသည် ခရိုင်တစ်ခုကို ကိုယ်စားပြုပြီး ဒေါ်လာ 50,000 အထက် ပျမ်းမျှအိမ်ထောင်စုဝင်ငွေရှိသော ခရိုင်များကို အပြာရောင်ဖြင့် ပြထားသည်ဟု ယူဆကြပါစို့။

Moran ၏ I = 0- ပျမ်းမျှအိမ်ထောင်စုဝင်ငွေသည် ကျပန်းကွဲပြားသည် (ဆိုလိုသည်မှာ ကျပန်းနယ်မြေများတွင် ကျပန်းအစုအဝေးများ)။

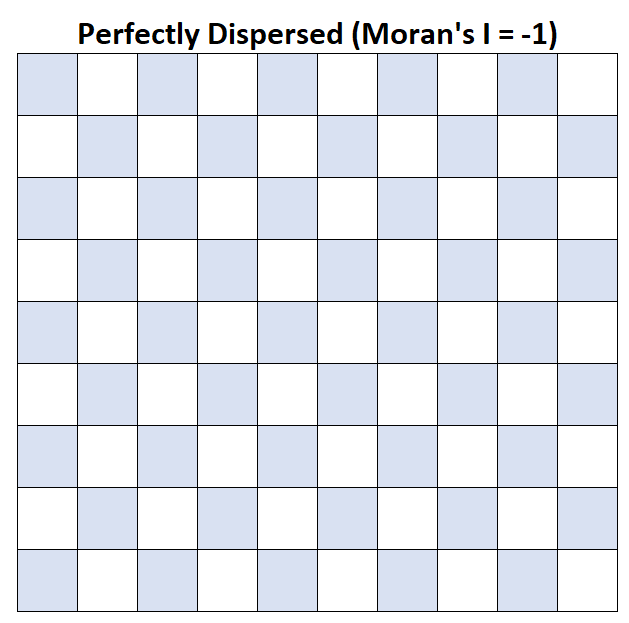
Moran ၏ I = -1- ပျမ်းမျှအိမ်ထောင်စုဝင်ငွေသည် လုံးဝကွဲပြားပါသည်။

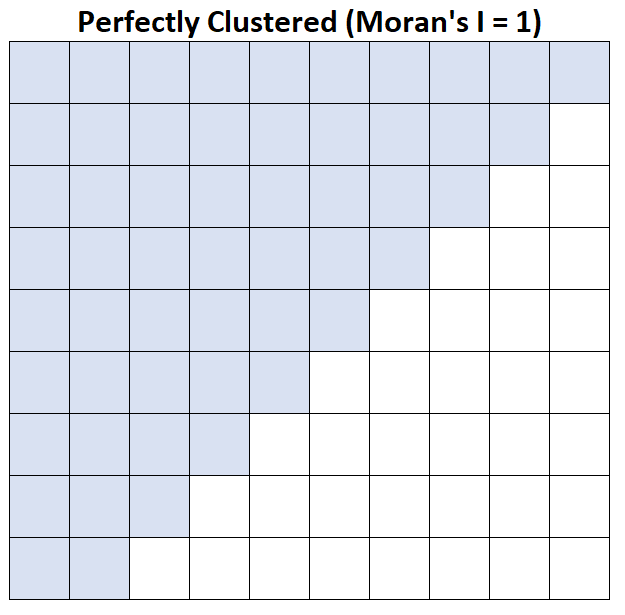
Moran ၏ I = 1- ပျမ်းမျှအိမ်ထောင်စုဝင်ငွေကို စုံလင်စွာအုပ်စုဖွဲ့ထားသည်။

စာရင်းအင်းဆော့ဖ်ဝဲလ် R တွင် Moran ၏ I ကို တွက်ချက်ခြင်း၏ ခိုင်မာသော ဥပမာတစ်ခုအတွက် ဤဥပမာကို ကိုးကားပါ။