Stata တွင် multicollinearity ကိုစမ်းသပ်နည်း

ဆုတ်ယုတ်မှုခွဲခြမ်းစိတ်ဖြာမှုတွင် Multicollinearity သည် ဆုတ်ယုတ်မှုပုံစံတွင် ထူးခြားသော သို့မဟုတ် အမှီအခိုကင်းသော အချက်အလက်များကို ပေးဆောင်ခြင်းမရှိသည့် နှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော ရှင်းပြချက်တစ်ခုနှင့်တစ်ခု တစ်ခုနှင့်တစ်ခု အလွန်ဆက်စပ်နေသောအခါတွင် ဖြစ်ပေါ်သည်။ ကိန်းရှင်များကြားတွင် ဆက်စပ်ဆက်စပ်မှုဒီဂရီသည် လုံလောက်စွာမြင့်မားပါက၊ ၎င်းသည် ဆုတ်ယုတ်မှုပုံစံကို အံဝင်ခွင်ကျဖြစ်စေပြီး အနက်ပြန်ဆိုရာတွင် ပြဿနာများဖြစ်စေနိုင်သည်။

ဥပမာအားဖြင့်၊ သင်သည် အောက်ပါကိန်းရှင်များနှင့်အတူ မျဉ်းကြောင်းပြန်ဆုတ်မှုများစွာကို လုပ်ဆောင်သည်ဆိုပါစို့။

ပြောင်းလဲနိုင်သော တုံ့ပြန်မှု- အများဆုံး ဒေါင်လိုက်ခုန်ခြင်း။

ရှင်းလင်းချက်ပြောင်းလွဲချက်များ- ဖိနပ်အရွယ်အစား၊ အမြင့်၊ လေ့ကျင့်ချိန်

ဤကိစ္စတွင်၊ အရပ်ရှည်သူများသည် ဖိနပ်အရွယ်အစား ပိုကြီးလေ့ရှိသောကြောင့် ဖိနပ်အရွယ်အစားနှင့် အမြင့်သည် ပြင်းထန်စွာ ဆက်စပ်မှုရှိနိုင်သည် ။ ဆိုလိုသည်မှာ multicollinearity သည် ဤဆုတ်ယုတ်မှုတွင် ပြဿနာတစ်ခု ဖြစ်နိုင်သည်ဟု ဆိုလိုသည်။

ကံကောင်းထောက်မစွာ၊ ဆုတ်ယုတ်မှုပုံစံတွင် ရှင်းပြထားသောကိန်းရှင်များကြားတွင် ဆက်စပ်မှုနှင့် ခိုင်ခံ့မှုကို တိုင်းတာသည့် variance inflation factor (VIF) ဟုခေါ်သော မက်ထရစ်ကို အသုံးပြု၍ multicollinearity ကို ရှာဖွေတွေ့ရှိနိုင်သည်။

Stata ရှိ ဆုတ်ယုတ်မှုဆိုင်ရာ ခွဲခြမ်းစိတ်ဖြာမှုတွင် ကော်လိုင်းပေါင်းစုံကို သိရှိရန် VIF ကိုအသုံးပြုပုံကို ဤသင်ခန်းစာတွင် ရှင်းပြထားသည်။

ဥပမာ- Stata တွင် ကော်လိုင်းပေါင်းစုံရှိမှု

ဤဥပမာအတွက်၊ ကျွန်ုပ်တို့သည် auto ဟုခေါ်သော Stata ၏ built-in ဒေတာအတွဲကို အသုံးပြုပါမည်။ ဒေတာအတွဲကို တင်ရန် အောက်ပါ command ကို သုံးပါ။

အလိုအလျောက်အသုံးပြုပါ။

တုံ့ပြန်မှု variable နှင့် အလေးချိန်၊ အလျားနှင့် mpg တို့ကို ရှင်းပြထားသော ကိန်းရှင်များအဖြစ် စျေးနှုန်းဖြင့် အမျိုးမျိုးသော linear regression model တစ်ခုနှင့် ကိုက်ညီရန် regress command ကို အသုံးပြုပါမည်။

regression price အလေးချိန် အရှည် စိုင်းစိုင်းခမ်းလှိုင်

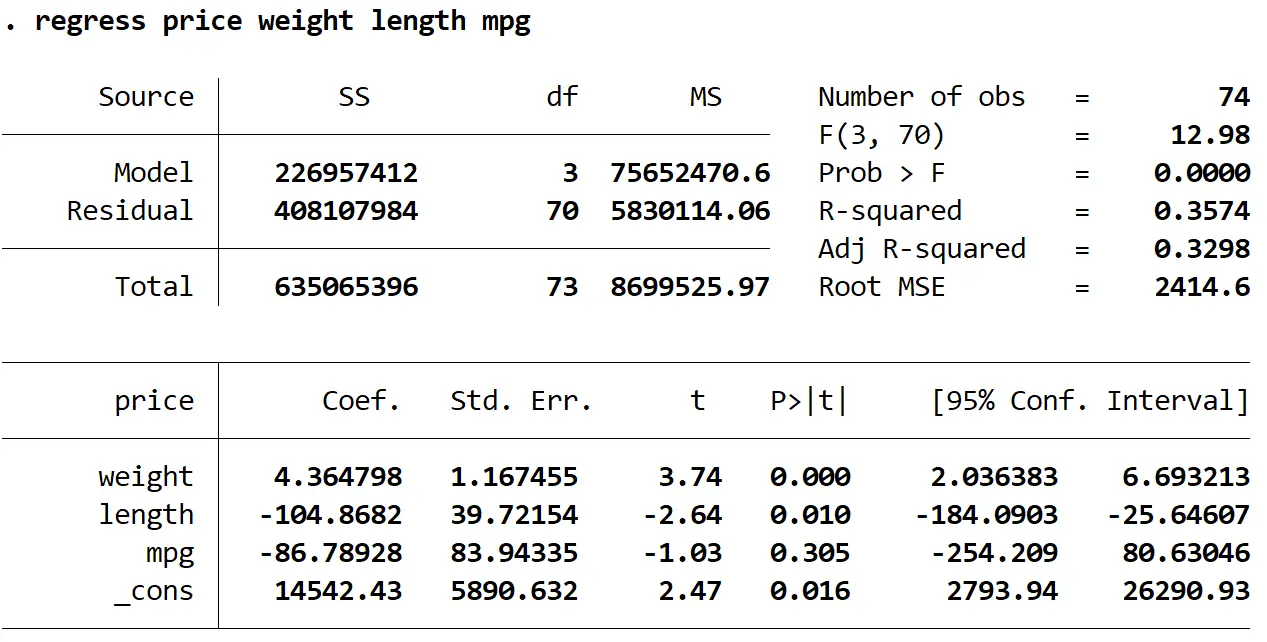
ထို့နောက်၊ ကျွန်ုပ်တို့သည် multicollinearity ကိုစမ်းသပ်ရန် vive command ကိုသုံးပါမည်။

အသက်ဝင်သည်။

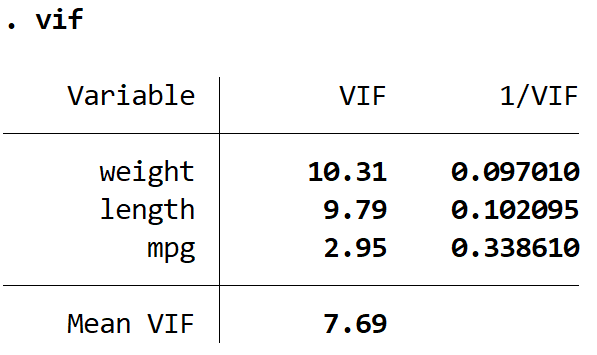
၎င်းသည် မော်ဒယ်ရှိ ရှင်းပြချက်တစ်ခုစီအတွက် VIF တန်ဖိုးကို ထုတ်ပေးသည်။ VIF တန်ဖိုးသည် 1 မှစတင်ပြီး အထက်ကန့်သတ်ချက်မရှိပါ။ VIF များကို ဘာသာပြန်ရန်အတွက် ယေဘူယျစည်းမျဉ်းမှာ-

• 1 ၏တန်ဖိုးသည် ပေးထားသောရှင်းပြချက်ကိန်းရှင်တစ်ခုနှင့် မော်ဒယ်ရှိ အခြားရှင်းပြကိန်းရှင်ကြားတွင် ဆက်စပ်မှုမရှိဟု ဖော်ပြသည်။
• 1 နှင့် 5 အကြားတန်ဖိုးသည် ပေးထားသောရှင်းပြချက်ကိန်းရှင်တစ်ခုနှင့် မော်ဒယ်ရှိ အခြားရှင်းပြကိန်းရှင်များကြားတွင် အလယ်အလတ်ဆက်စပ်မှုကို ညွှန်ပြသော်လည်း အထူးသတိထားရန် လိုအပ်လောက်အောင် မပြင်းထန်ပါ။
• 5 ထက်ကြီးသောတန်ဖိုးသည် ပေးထားသောရှင်းပြချက်ကိန်းရှင်နှင့် မော်ဒယ်ရှိ အခြားရှင်းပြကိန်းရှင်များအကြား ပြင်းထန်စွာဆက်စပ်မှုကို ညွှန်ပြသည်။ ဤကိစ္စတွင်၊ ဆုတ်ယုတ်မှုရလဒ်များတွင် ကိန်းဂဏန်းခန့်မှန်းချက်များနှင့် p-တန်ဖိုးများသည် ယုံကြည်စိတ်ချရဖွယ်မရှိပေ။

အလေးချိန်နှင့် အလျားအတွက် VIF တန်ဖိုးများသည် 5 ထက် ပိုများသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်၊၊ multicollinearity သည် regression model တွင် ပြဿနာတစ်ခုဖြစ်နိုင်သည်ဟု ညွှန်ပြပါသည်။

Multicollinearity ကို ဘယ်လိုကိုင်တွယ်မလဲ။

Multicollinearity ကို ကိုင်တွယ်ရန် အလွယ်ဆုံးနည်းလမ်းမှာ ပြဿနာ variable များထဲမှ တစ်ခုကို ဖယ်ရှားရန်ဖြစ်ပြီး၊ သင်ဖယ်ရှားနေသော variable သည် မည်သို့ပင်ဖြစ်စေ မလိုအပ်တော့ဘဲ မော်ဒယ်သို့ ထူးခြားသော သို့မဟုတ် အမှီအခိုကင်းသော အချက်အလက်အနည်းငယ်ကို ပေါင်းထည့်သောကြောင့် ဖြစ်သည်။

မည်သည့် variable များကို ဖယ်ရှားရမည်ကို ဆုံးဖြတ်ရန်အတွက်၊ ကျွန်ုပ်တို့သည် model ရှိ variable တစ်ခုစီကြားရှိ ဆက်စပ်ကိန်းများကို ပြသရန် corr command ကိုအသုံးပြု၍ corr command ကိုအသုံးပြု၍ model ရှိ variable တစ်ခုစီ၏ correlation coefficients ကိုပြသရန်၊ Multicollinearity ပြဿနာ-

corr ဈေးနှုန်း အလေးချိန် အရှည် စိုင်းစိုင်းခမ်းလှိုင်

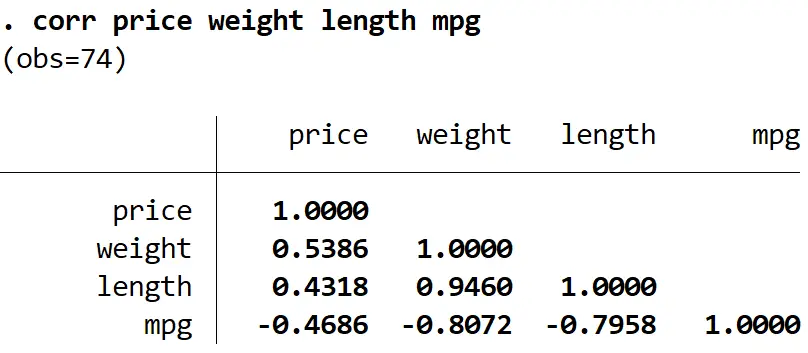
အရှည်သည် အလေးချိန်နှင့် mpg နှစ်ခုလုံးနှင့် အလွန်ဆက်စပ်နေကြောင်း ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပြီး၊ တုံ့ပြန်မှုပြောင်းလဲနိုင်သောစျေးနှုန်းနှင့် အနိမ့်ဆုံးဆက်စပ်မှုရှိသည်။ ထို့ကြောင့်၊ မော်ဒယ်အလျားကို ဖယ်ရှားခြင်းသည် ဆုတ်ယုတ်မှုမော်ဒယ်၏ အလုံးစုံအရည်အသွေးကို လျှော့ချခြင်းမရှိဘဲ multicollinearity ပြဿနာကို ဖြေရှင်းနိုင်သည်။

၎င်းကို စမ်းသပ်ရန်အတွက်၊ အလေးချိန်နှင့် mpg တို့ကို ရှင်းပြထားသော ကိန်းရှင်များအဖြစ် အသုံးပြု၍ ဆုတ်ယုတ်မှုခွဲခြမ်းစိတ်ဖြာမှုကို ထပ်မံလုပ်ဆောင်နိုင်သည်-

regression price စိုင်းစိုင်းခမ်းလှိုင် အလေးချိန်

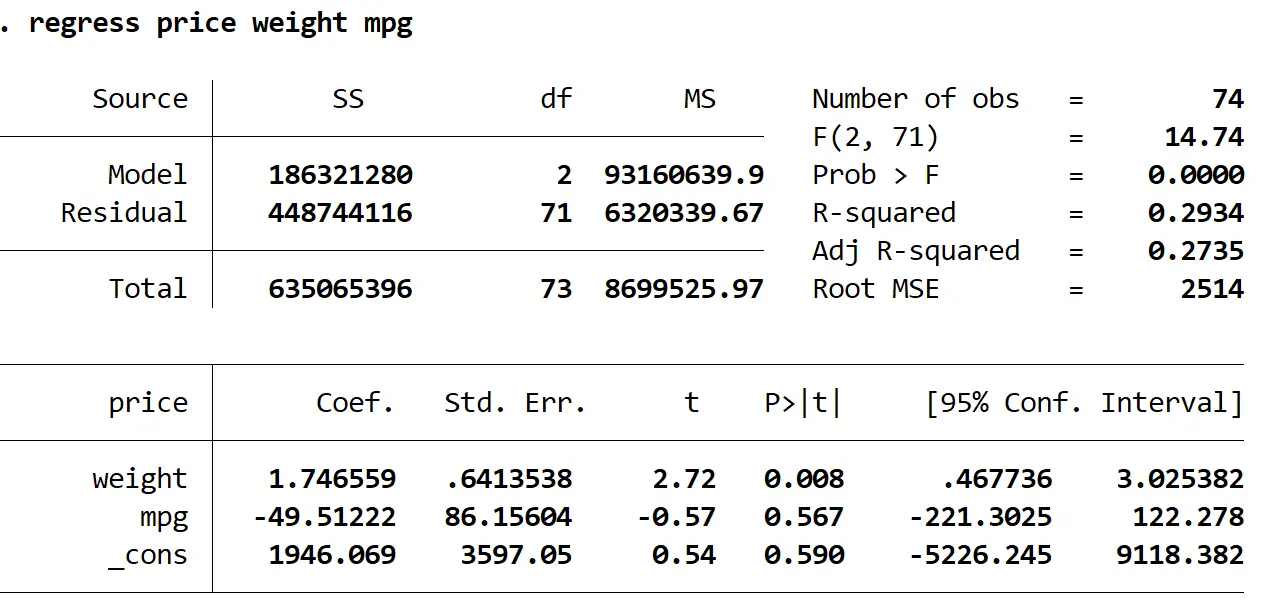
ဤမော်ဒယ်၏ ချိန်ညှိထားသော R-squared သည် ယခင်မော်ဒယ်ရှိ 0.3298 နှင့် နှိုင်းယှဉ်ပါက 0.2735 ဖြစ်သည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။ ၎င်းသည် မော်ဒယ်၏ အလုံးစုံ အသုံးဝင်မှု အနည်းငယ်သာ လျော့နည်းသွားကြောင်း ညွှန်ပြသည်။ ထို့နောက် VIF အမိန့်ကို အသုံးပြု၍ VIF တန်ဖိုးများကို ကျွန်ုပ်တို့ ရှာဖွေနိုင်သည်-

သွက်လက်သည်။

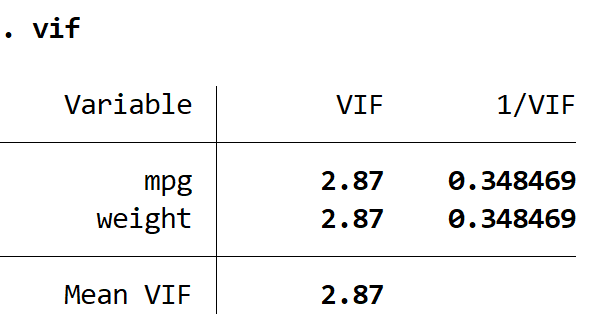
VIF တန်ဖိုးနှစ်ခုလုံးသည် 5 ထက်နည်းသောကြောင့် multicollinearity သည် model တွင်ပြဿနာမရှိတော့ကြောင်းဖော်ပြသည်။