Multiple linear regression ၏ ယူဆချက်ငါးခု

Multiple linear regression သည် များစွာသော ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် တုံ့ပြန်မှု variable အကြား ဆက်နွယ်မှုကို နားလည်ရန် ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည့် ကိန်းဂဏန်းဆိုင်ရာ နည်းလမ်းတစ်ခုဖြစ်သည်။

သို့သော်၊ မျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှု အများအပြားကို မလုပ်ဆောင်မီ၊ ကျွန်ုပ်တို့သည် ယူဆချက်ငါးခု ပြည့်မီကြောင်း ဦးစွာ သေချာစွာ စစ်ဆေးရပါမည်။

1. Linear ဆက်ဆံရေး- ခန့်မှန်းသူ ကိန်းရှင် တစ်ခုစီနှင့် တုံ့ပြန်မှု ကိန်းရှင်တို့ကြား မျဉ်းဖြောင့် ဆက်စပ်မှု ရှိပါသည်။

2. Multicollinearity မရှိ- ကြိုတင်ခန့်မှန်းကိန်းရှင်များ တစ်ခုမှ တစ်ခုနှင့်တစ်ခု အလွန်ဆက်စပ်မှုမရှိပါ။

3. လွတ်လပ်ရေး- လေ့လာတွေ့ရှိချက်များသည် သီးခြားဖြစ်သည်။

4. Homoscedasticity- အကြွင်းအကျန်များသည် linear model ၏ အမှတ်တစ်ခုစီတွင် အဆက်မပြတ်ကွဲလွဲမှုရှိသည်။

5. Multivariate normality- မော်ဒယ်အကြွင်းအကျန်များကို ပုံမှန်အတိုင်း ဖြန့်ဝေပါသည်။

အကယ်၍ ဤယူဆချက်တစ်ခု သို့မဟုတ် တစ်ခုထက်ပို၍ မကိုက်ညီပါက၊ linear regression အများအပြား၏ရလဒ်များသည် ယုံကြည်စိတ်ချရမည်မဟုတ်ပေ။

ဤဆောင်းပါးတွင်၊ ယူဆချက်တစ်ခုစီအတွက် ရှင်းလင်းချက်၊ ယူဆချက်နှင့်ကိုက်ညီခြင်းရှိ၊ မရှိ ဆုံးဖြတ်နည်းနှင့် ယူဆချက်မပြည့်မီပါက ဘာလုပ်ရမည်နည်း။

Hypothesis 1- Linear ဆက်ဆံရေး

Multiple linear regression သည် ခန့်မှန်းသူ variable တစ်ခုစီနှင့် response variable အကြား linear ဆက်နွယ်မှုရှိသည်ဟု ယူဆသည်။

ဒီယူဆချက်နဲ့ ကိုက်ညီမှုရှိမရှိ ဘယ်လိုဆုံးဖြတ်မလဲ။

ဤယူဆချက်နှင့်ကိုက်ညီခြင်းရှိမရှိ ဆုံးဖြတ်ရန် အရိုးရှင်းဆုံးနည်းလမ်းမှာ ခန့်မှန်းသူကိန်းရှင်တစ်ခုစီ၏ ကွဲလွဲချက်တစ်ခုနှင့် တုံ့ပြန်မှုကိန်းရှင်ကို ဖန်တီးရန်ဖြစ်သည်။

၎င်းသည် ကိန်းရှင်နှစ်ခုကြားတွင် linear ဆက်နွယ်မှုရှိမရှိကို မြင်သာစွာမြင်နိုင်စေပါသည်။

scatterplot ရှိ အမှတ်များသည် ဖြောင့်ထောင့်ဖြတ်မျဉ်းတစ်လျှောက် ခန့်မှန်းခြေအားဖြင့် တည်ရှိနေပါက၊ ကိန်းရှင်များကြားတွင် မျဉ်းကြောင်းဆက်နွယ်မှုရှိနိုင်ဖွယ်ရှိသည်။

ဥပမာအားဖြင့်၊ အောက်ပါဂရပ်ရှိ အမှတ်များသည် မျဉ်းဖြောင့်ပေါ်တွင် ကျရောက်နေပုံရပြီး၊ ဤအထူးဟောကိန်းရှင်ကိန်းရှင် (x) နှင့် တုံ့ပြန်မှုကိန်းရှင် (y) အကြား မျဉ်းကြောင်းဆက်နွယ်မှုရှိကြောင်း ညွှန်ပြနေပါသည်။

ဒီယူဆချက်ကို မလေးစားရင် ဘာလုပ်မလဲ။

ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကိန်းရှင်များနှင့် တုံ့ပြန်မှုကိန်းရှင်တို့ကြား မျဉ်းဖြောင့်ဆက်နွယ်မှုမရှိပါက၊ ကျွန်ုပ်တို့တွင် ရွေးချယ်စရာများစွာရှိသည်-

1. မှတ်တမ်း သို့မဟုတ် စတုရန်း အမြစ်ကိုယူခြင်း ဥပမာအားဖြင့် ခန့်မှန်းသူကိန်းရှင်သို့ မျဉ်းကြောင်းမဟုတ်သောအသွင်ပြောင်းခြင်းကို အသုံးချပါ။ ၎င်းသည် ဆက်ဆံရေးကို ပိုမိုမျဉ်းဖြောင့်တစ်ခုအဖြစ်သို့ ပြောင်းလဲသွားစေနိုင်သည်။

2. မော်ဒယ်သို့ နောက်ထပ် ကြိုတင်ခန့်မှန်းကိန်းရှင်ကို ထည့်ပါ။ ဥပမာ၊ x နှင့် y ၏ကွက်လပ်တွင် parabolic ပုံသဏ္ဍာန်ရှိပါက၊ X ² ကို မော်ဒယ်ရှိ ထပ်လောင်းကြိုတင်ခန့်မှန်းကိန်းရှင်အဖြစ် ထပ်ထည့်ခြင်းသည် အဓိပ္ပာယ်ရှိပေမည်။

3. ခန့်မှန်းသူကိန်းရှင်ကို မော်ဒယ်မှ ဖယ်ရှားပါ။ အပြင်းထန်ဆုံး အခြေအနေတွင်၊ အချို့သော ခန့်မှန်းသူကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်ကြား မျဉ်းကြောင်းဆက်နွယ်မှု မရှိပါက၊ မော်ဒယ်တွင် ခန့်မှန်းသူကိန်းရှင်ကို ထည့်သွင်းရန် အသုံးဝင်မည်မဟုတ်ပေ။

အယူအဆ 2- ပေါင်းစပ်ဖွဲ့စည်းမှု မရှိပါ။

Multiple linear regression သည် ကြိုတင်ခန့်မှန်းသည့်ကိန်းရှင်တစ်ခုမှ တစ်ခုနှင့်တစ်ခု အလွန်ဆက်စပ်မှုမရှိဟု ယူဆသည်။

တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကြိုတင်ခန့်မှန်းကိန်းရှင်များသည် အလွန်ဆက်နွယ်နေသောအခါ၊ ဆုတ်ယုတ်မှုပုံစံသည် multicollinearity ကို ခံစားရပြီး မော်ဒယ်၏ ဖော်ကိန်းခန့်မှန်းချက်များကို ယုံကြည်စိတ်ချမှုမရှိစေပါ။

ဒီယူဆချက်နဲ့ ကိုက်ညီမှုရှိမရှိ ဘယ်လိုဆုံးဖြတ်မလဲ။

ဤယူဆချက်နှင့် ကိုက်ညီမှုရှိမရှိ ဆုံးဖြတ်ရန် အရိုးရှင်းဆုံးနည်းလမ်းမှာ ခန့်မှန်းသူကိန်းရှင်တစ်ခုစီအတွက် VIF တန်ဖိုးကို တွက်ချက်ခြင်းဖြစ်သည်။

VIF တန်ဖိုးများသည် 1 မှစတင်ပြီး အထက်ကန့်သတ်ချက်မရှိပါ။ ယေဘုယျအားဖြင့်၊ 5* အထက်ရှိ VIF တန်ဖိုးများသည် အလားအလာရှိသော multicollinearity ကိုဖော်ပြသည်။

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် စာရင်းအင်းဆော့ဖ်ဝဲအမျိုးမျိုးတွင် VIF တွက်ချက်နည်းကို ပြသသည်-

• R ဖြင့် VIF တွက်နည်း
• Python တွင် VIF တွက်နည်း
• Excel တွင် VIF တွက်ချက်နည်း

* တစ်ခါတစ်ရံ သုတေသီများသည် လေ့လာမှုနယ်ပယ်ပေါ်မူတည်၍ VIF တန်ဖိုး 10 ကို အသုံးပြုသည်။

ဒီယူဆချက်ကို မလေးစားရင် ဘာလုပ်မလဲ။

တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကိန်းရှင်များတွင် VIF တန်ဖိုး 5 ထက်များပါက၊ ဤပြဿနာကို ဖြေရှင်းရန် အလွယ်ကူဆုံးနည်းလမ်းမှာ မြင့်မားသော VIF တန်ဖိုးများဖြင့် ခန့်မှန်းသူကိန်းရှင်(များ) ကို ဖယ်ရှားရန်ဖြစ်သည်။

တနည်းအားဖြင့်၊ အကယ်၍ သင်သည် မော်ဒယ်တွင် ခန့်မှန်းပေးသူ ကိန်းရှင်တစ်ခုစီကို ထိန်းသိမ်းထားလိုပါက၊ အလွန်ဆက်စပ်နေသော ခန့်မှန်းသူကိန်းရှင်များကို ကိုင်တွယ်ရန် ဒီဇိုင်းထုတ်ထားသော ခေါင်ဆုတ်ယုတ်မှု ၊ lasso ဆုတ်ယုတ်မှု သို့မဟုတ် တစ်စိတ်တစ်ပိုင်း အနည်းဆုံးစတုရန်းဆုတ်ယုတ်မှု ကဲ့သို့သော ကွဲပြားသောကိန်းဂဏန်းအချက်အလက်များကို အသုံးပြုနိုင်သည်။

အယူအဆ 3- လွတ်လပ်ရေး

Multiple linear regression သည် data set တစ်ခုစီရှိ စောင့်ကြည့်မှုတစ်ခုစီသည် သီးခြားဖြစ်ကြောင်း ယူဆသည်။

ဒီယူဆချက်နဲ့ ကိုက်ညီမှုရှိမရှိ ဘယ်လိုဆုံးဖြတ်မလဲ။

ဤယူဆချက်နှင့်ကိုက်ညီခြင်းရှိမရှိ ဆုံးဖြတ်ရန် အရိုးရှင်းဆုံးနည်းလမ်းမှာ Durbin-Watson စမ်းသပ်မှု တစ်ခုဖြစ်ပြီး ကျန်ရှိသော (ထို့ကြောင့် လေ့လာတွေ့ရှိချက်များ) သည် autocorrelation ရှိမရှိကိုပြသသည့် တရားဝင်စာရင်းအင်းစစ်ဆေးမှုတစ်ခုဖြစ်သည်။

ဒီယူဆချက်ကို မလေးစားရင် ဘာလုပ်မလဲ။

ဤယူဆချက်ကို မည်ကဲ့သို့ ချိုးဖောက်သည်အပေါ်မူတည်၍ သင့်တွင် ရွေးချယ်စရာများစွာရှိသည်-

• အပြုသဘောဆောင်သော အမှတ်စဉ်ဆက်နွှယ်မှုအတွက်၊ မော်ဒယ်သို့ မှီခိုမှုနှင့်/သို့မဟုတ် အမှီအခိုကင်းသော ကိန်းရှင်၏ နောက်ကျကျန်နေမှုများကို ထည့်သွင်းစဉ်းစားပါ။
• အနှုတ်အမှတ်စဉ်ဆက်နွယ်မှုအတွက်၊ သင့် variable များထဲမှ တစ်ခုမျှ နှောင့်နှေးနေမည်မဟုတ်ကြောင်း သေချာပါစေ။
• ရာသီအလိုက်ဆက်စပ်မှုအတွက်၊ မော်ဒယ်သို့ ရာသီအလိုက် အရုပ်များကို ထည့်စဉ်းစားပါ။

အယူအဆ ၄- လိင်တူဆက်ဆံခြင်း

မျဉ်းကြောင်းကြောင်း ဆုတ်ယုတ်မှု အများအပြားသည် အကြွင်းအကျန်များသည် မျဉ်းနားပုံစံရှိ အမှတ်တစ်ခုစီတွင် အဆက်မပြတ်ကွဲလွဲမှုရှိသည်ဟု ယူဆသည်။ ဒီလိုမှမဟုတ်ရင် ကျန်တဲ့သူတွေဟာ မျိုးကွဲတွေ ကွဲကုန်တယ်။

ဆုတ်ယုတ်မှု ခွဲခြမ်းစိတ်ဖြာမှုတွင် မျိုးကွဲကွဲပြားမှု ရှိနေသောအခါ၊ ဆုတ်ယုတ်မှုပုံစံ၏ ရလဒ်များသည် ယုံကြည်ရလောက်အောင် ဖြစ်လာသည်။

အထူးသဖြင့်၊ heteroskedasticity သည် regression coefficient ခန့် မှန်းချက်များ၏ ကွဲလွဲမှုကို တိုးစေသည်၊ သို့သော် regression model သည် ၎င်းအတွက် ထည့်မတွက်ပါ။ ၎င်းသည် ဆုတ်ယုတ်မှုပုံစံသည် မော်ဒယ်ရှိ ကိန်းဂဏာန်းတစ်ခုသည် ကိန်းဂဏန်းအရ သိသာထင်ရှားသည်ဟု ဆိုနိုင်သည်၊ လက်တွေ့တွင် ၎င်းမဟုတ်သည့်အခါတွင် ပို၍ဖြစ်နိုင်ချေရှိသည်။

ဒီယူဆချက်နဲ့ ကိုက်ညီမှုရှိမရှိ ဘယ်လိုဆုံးဖြတ်မလဲ။

ဤယူဆချက်နှင့် ကိုက်ညီခြင်းရှိမရှိ ဆုံးဖြတ်ရန် အလွယ်ဆုံးနည်းလမ်းမှာ ခန့်မှန်းတန်ဖိုးများနှင့် စံသတ်မှတ်ထားသော ကျန်ရှိသောကွက်ကွက်တစ်ခုကို ဖန်တီးရန်ဖြစ်သည်။

သင်သည် ဆုတ်ယုတ်မှုပုံစံကို ဒေတာအတွဲတစ်ခုနှင့် အံဝင်ခွင်ကျဖြစ်စေပြီးသည်နှင့် x-ဝင်ရိုးပေါ်ရှိ တုံ့ပြန်မှုကိန်းရှင်၏ ခန့်မှန်းတန်ဖိုးများနှင့် x-ဝင်ရိုးပေါ်ရှိ မော်ဒယ်၏ စံသတ်မှတ်ထားသော အကြွင်းအကျန်များကို ပြသသည့် ဖြန့်ခွဲမှုတစ်ခုကို ဖန်တီးနိုင်သည်။ y

ခွဲခြမ်းစိတ်ဖြာမှုရှိ အမှတ်များသည် လမ်းကြောင်းတစ်ခု ပေါ်နေပါက၊ heteroscedasticity ရှိနေပါသည်။

အောက်ဖော်ပြပါဇယားသည် heteroskedasticity သည် ပြဿနာမဟုတ်သည့် ဆုတ်ယုတ်မှုပုံစံ၏ ဥပမာကို ပြသည်-

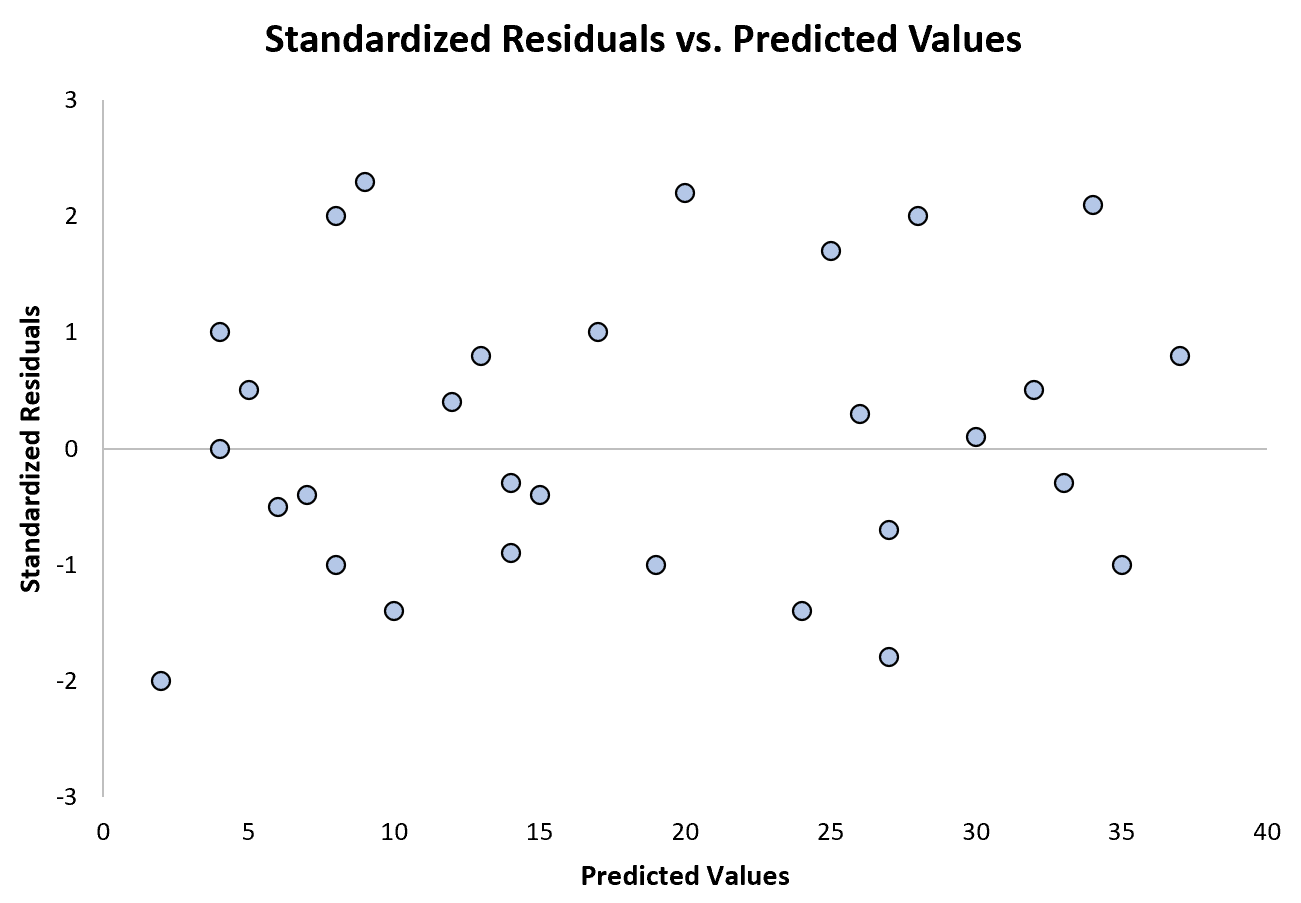
စံသတ်မှတ်ထားသော အကြွင်းအကျန်များသည် ရှင်းလင်းသောပုံစံမရှိဘဲ သုညတွင် ပြန့်ကျဲနေသည်ကို သတိပြုပါ။

အောက်ဖော်ပြပါဇယားသည် heteroscedasticity ပြဿနာ ရှိ သည့် ဆုတ်ယုတ်မှုပုံစံ၏ ဥပမာကို ပြသည်-

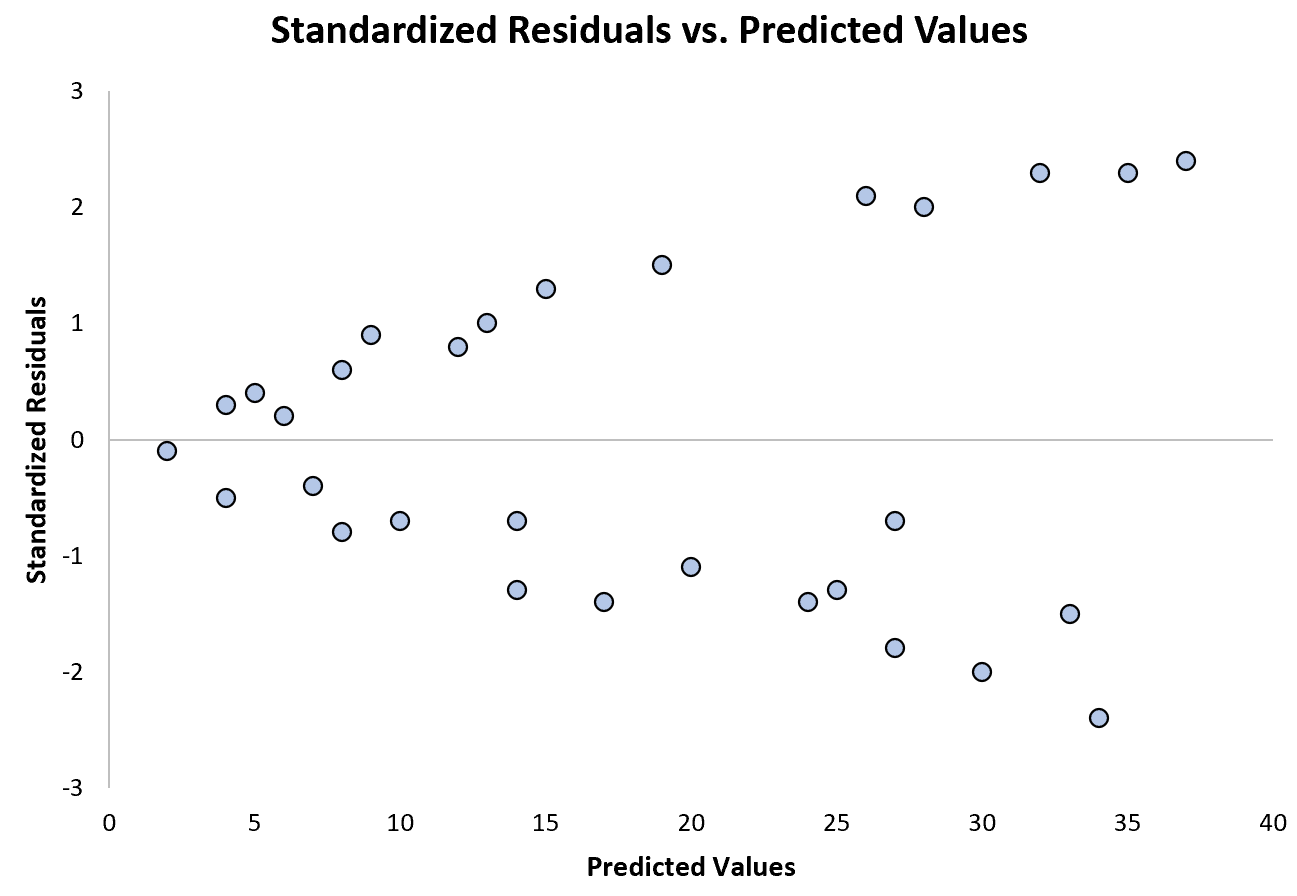
ခန့်မှန်းတန်ဖိုးများ တိုးလာသည်နှင့်အမျှ စံချိန်စံညွှန်းသတ်မှတ်ထားသော အကြွင်းအကျန်များ မည်ကဲ့သို့ ပိုမိုပျံ့နှံ့လာသည်ကို သတိပြုပါ။ ဤ “ပုံး” ပုံသဏ္ဍာန်သည် မျိုးရိုးလိုက်ခြင်း၏ ဂန္တဝင်လက္ခဏာတစ်ရပ်ဖြစ်သည်-

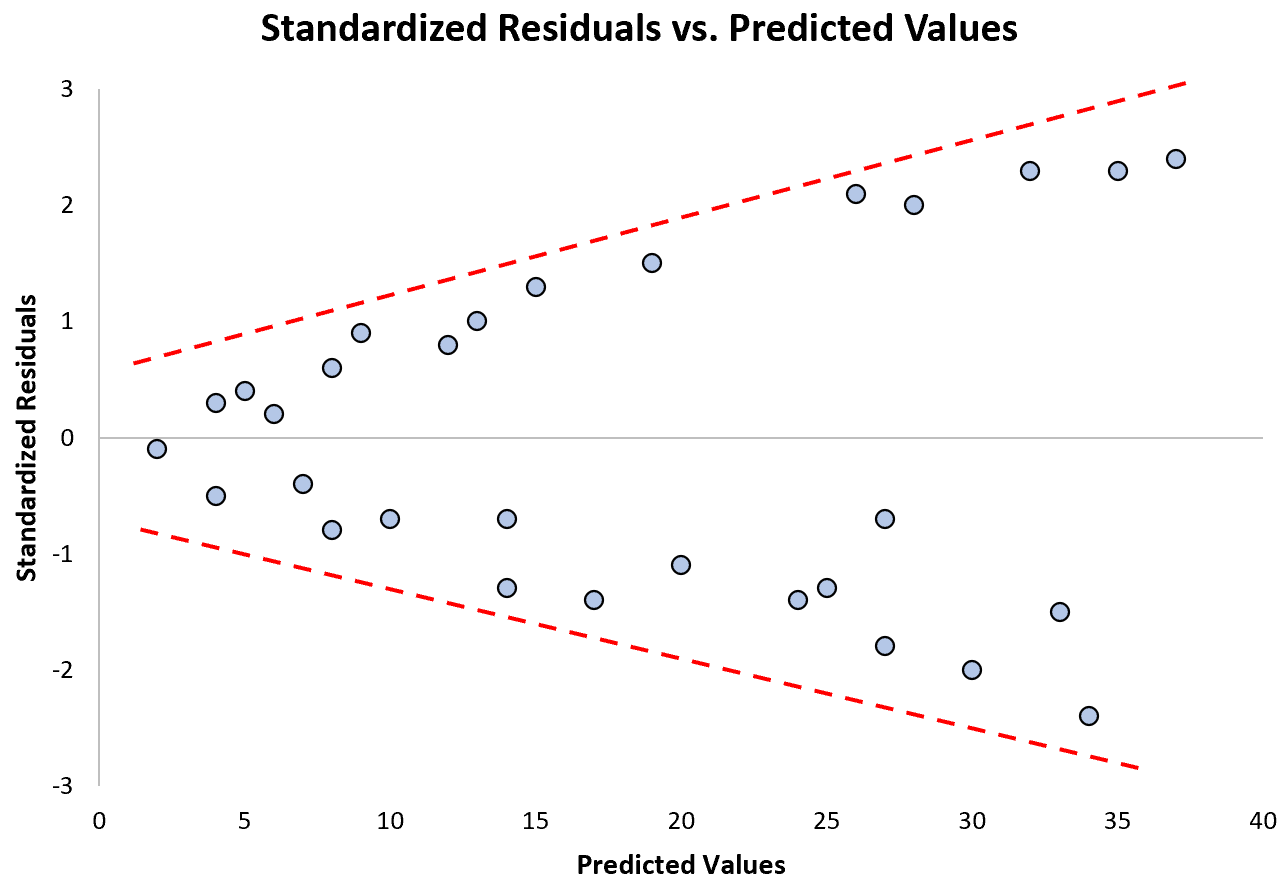
ဒီယူဆချက်ကို မလေးစားရင် ဘာလုပ်မလဲ။

heteroskedasticity အတွက် ပြင်ရန် ဘုံသုံးနည်း ရှိပါသည်။

1. တုံ့ပြန်မှုကိန်းရှင်ကို ပြောင်းလဲပါ။ heteroskedasticity ကိုကိုင်တွယ်ရန် အသုံးအများဆုံးနည်းလမ်းမှာ response variable ၏တန်ဖိုးအားလုံး၏ log, square root, သို့မဟုတ် cube root ကိုယူခြင်းဖြင့် တုံ့ပြန်မှု variable ကိုအသွင်ပြောင်းရန်ဖြစ်သည်။ ယင်းသည် မကြာခဏဆိုသလို မျိုးရိုးဗီဇ ပျောက်ကွယ်သွားစေသည်။

2. တုံ့ပြန်မှုပုံစံကို ပြန်လည်သတ်မှတ်ပါ။ တုံ့ပြန်မှုကိန်းရှင်ကို ပြန်လည်သတ်မှတ်ရန် နည်းလမ်းတစ်ခုမှာ ကုန်ကြမ်းတန်ဖိုးထက် နှုန်းကို အသုံးပြုခြင်းဖြစ်သည်။ ဥပမာအားဖြင့်၊ မြို့တွင်းရှိ ပန်းဆရာအရေအတွက်ကို ခန့်မှန်းရန် လူဦးရေအရွယ်အစားကို အသုံးပြုမည့်အစား၊ တစ်ဦးချင်းအလိုက် ပန်းဆရာအရေအတွက်ကို ခန့်မှန်းရန် လူဦးရေအရွယ်အစားကို အသုံးပြုနိုင်သည်။

ကိစ္စအများစုတွင်၊ ကျွန်ုပ်တို့သည် ပန်းသမားအရေအတွက်ထက် လူတစ်ဦးလျှင် ပန်းဆရာအရေအတွက်ကို တိုင်းတာနေသောကြောင့် ပိုမိုကြီးမားသောလူဦးရေအတွင်း သဘာဝအတိုင်းဖြစ်ပေါ်သည့် ကွဲပြားမှုကို လျော့နည်းစေသည်။

3. အလေးချိန် ဆုတ်ယုတ်မှုကို သုံးပါ။ heteroscedasticity အတွက် ပြုပြင်ရန် အခြားနည်းလမ်းမှာ ၎င်း၏ တပ်ဆင်ထားသော တန်ဖိုး၏ ကွဲလွဲမှုအပေါ် အခြေခံ၍ ဒေတာအမှတ်တစ်ခုစီအတွက် အလေးချိန်ကို သတ်မှတ်ပေးသည့် အလေးချိန် ဆုတ်ယုတ်မှုကို အသုံးပြုခြင်းဖြစ်သည်။

အခြေခံအားဖြင့်၊ ၎င်းသည် ၎င်းတို့ကျန်ရှိသော စတုရန်းများကို လျှော့ချပြီး ကွဲပြားမှုများ ပိုမိုမြင့်မားသည့် ဒေတာအမှတ်များကို နည်းပါးစေသည်။ သင့်လျော်သောအလေးချိန်များကိုအသုံးပြုသောအခါ၊ ၎င်းသည် မျိုးကွဲခြင်းပြဿနာကို ဖယ်ရှားပေးနိုင်သည်။

ဆက်စပ် : R တွင် အလေးချိန် ဆုတ်ယုတ်မှု ကို မည်သို့ လုပ်ဆောင်ရမည်

ယူဆချက် 4- ပုံမှန်ပုံစံမျိုးစုံ

မျဉ်းကြောင်းပြန်ဆုတ်မှုများစွာသည် မော်ဒယ်အကြွင်းအကျန်များကို ပုံမှန်အားဖြင့် ဖြန့်ဝေသည်ဟု ယူဆသည်။

ဒီယူဆချက်နဲ့ ကိုက်ညီမှုရှိမရှိ ဘယ်လိုဆုံးဖြတ်မလဲ။

ဤယူဆချက်အား ကျေနပ်မှုရှိမရှိ စစ်ဆေးရန် ဘုံနည်းလမ်း နှစ်ခုရှိသည်။

1. QQ ကွက်များကို အသုံးပြု၍ အယူအဆကို အမြင်အာရုံဖြင့် စစ်ဆေးပါ ။

QQ ကွက်ကွက်သည် ပမာဏ-အရေအတွက် အတိုကောက်ဖြစ်ပြီး၊ မော်ဒယ်တစ်ခု၏ အကြွင်းအကျန်များသည် ပုံမှန်ဖြန့်ဝေမှုအတိုင်း လိုက်နာခြင်း ရှိ၊ မရှိ ဆုံးဖြတ်ရန် ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည့် ကွက်အမျိုးအစားတစ်ခုဖြစ်သည်။ ကွက်ကွက်ပေါ်ရှိ အမှတ်များသည် အကြမ်းဖျင်းအားဖြင့် တည့်တည့် ထောင့်ဖြတ်မျဉ်းများ ဖြစ်ပေါ်လာပါက၊ ပုံမှန်အဖြစ် ယူဆချက်နှင့် ကိုက်ညီပါသည်။

အောက်ဖော်ပြပါ QQ ကွက်ကွက်သည် အကြမ်းဖျင်းအားဖြင့် ပုံမှန်ဖြန့်ဖြူးမှုနောက်ဆက်တွဲဖြစ်သော ကျန်အကြွင်းအကျန်များကို နမူနာပြသည်-

သို့သော်၊ အောက်ဖော်ပြပါ QQ ကွက်ကွက်သည် အကြွင်းအကျန်များသည် ဖြောင့်ထောင့်ဖြတ်မျဉ်းမှ ရှင်းရှင်းလင်းလင်း သွေဖည်သွားသည့် ကိစ္စတစ်ခု၏ ဥပမာကို ပြသထားပြီး ၎င်းတို့သည် ပုံမှန်ဖြန့်ဖြူးမှုကို မလိုက်နာကြောင်း ညွှန်ပြသည်-

2. Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre, သို့မဟုတ် D’Agostino-Pearson ကဲ့သို့သော တရားဝင် ကိန်းဂဏန်းစမ်းသပ်မှုတစ်ခုကို အသုံးပြု၍ အယူအဆကို အတည်ပြုပါ။

ဤစစ်ဆေးမှုများသည် ကြီးမားသောနမူနာအရွယ်အစားအတွက် အထိခိုက်မခံကြောင်း မှတ်သားထားပါ – ဆိုလိုသည်မှာ၊ သင်၏နမူနာအရွယ်အစား အလွန်ကြီးမားသောအခါ ကျန်ရှိသည့်အရာများသည် ပုံမှန်မဟုတ်ကြောင်း မကြာခဏ ကောက်ချက်ချလေ့ရှိပါသည်။ ထို့ကြောင့် ဤယူဆချက်အား အတည်ပြုရန် QQ ကြံစည်မှုကဲ့သို့ ဂရပ်ဖစ်နည်းလမ်းများကို အသုံးပြုရန် မကြာခဏ ပိုမိုလွယ်ကူရခြင်း ဖြစ်သည်။

ဒီယူဆချက်ကို မလေးစားရင် ဘာလုပ်မလဲ။

ပုံမှန်ဖြစ်ရိုးဖြစ်စဉ် ယူဆချက်နှင့် မကိုက်ညီပါက၊ သင့်တွင် ရွေးချယ်စရာများစွာရှိသည်။

1. ပထမဦးစွာ၊ ပုံမှန်ဖြစ်ရိုးဖြစ်စဉ်ယူဆချက်အား ချိုးဖောက်မှုဖြစ်စေသည့် ဒေတာများတွင် လွန်ကဲသောအစွန်းအထင်းများမရှိကြောင်း စစ်ဆေးပါ။

2. ထို့နောက် သင်သည် တုံ့ပြန်မှု variable ၏ နှစ်ထပ်ကိန်း၊ မှတ်တမ်း သို့မဟုတ် cube root ကို ယူခြင်းဖြင့် တုံ့ပြန်မှု variable သို့ လိုင်းမဟုတ်သောအသွင်ပြောင်းခြင်းကို အသုံးချနိုင်သည်။ ၎င်းသည် မော်ဒယ်အကြွင်းအကျန်များကို သာမန်ထက်ပို၍ ဖြန့်ဖြူးပေးလေ့ရှိသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် မျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှု အများအပြားနှင့် ၎င်း၏ ယူဆချက်များနှင့် ပတ်သက်သော နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

Multiple Linear Regression အကြောင်း နိဒါန်း
Regression ခွဲခြမ်းစိတ်ဖြာမှုတွင် Heteroskedasticity အတွက်လမ်းညွှန်
Regression ရှိ Multicollinearity နှင့် VIF အတွက်လမ်းညွှန်

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် မတူညီသော ကိန်းဂဏန်းဆိုင်ရာဆော့ဖ်ဝဲလ်ကို အသုံးပြု၍ မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းကို အဆင့်ဆင့်လုပ်ဆောင်ပုံ ဥပမာများကို ဖော်ပြပေးသည်-

Excel တွင် linear regression အများအပြားလုပ်ဆောင်နည်း
R တွင် linear regression အများအပြားလုပ်ဆောင်နည်း
SPSS တွင် မျဉ်းကြောင်း ဆုတ်ယုတ်မှု အများအပြားကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
Stata တွင် မျဉ်းကြောင်းကြောင်း ဆုတ်ယုတ်မှု အများအပြားကို လုပ်ဆောင်နည်း