မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းရလဒ်များကို r တွင် အများအပြားချနည်း

ကျွန်ုပ်တို့သည် R တွင် ရိုးရှင်းသော မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းကို လုပ်ဆောင်သောအခါ၊ ကျွန်ုပ်တို့သည် ခန့်မှန်းသူကိန်းရှင်တစ်ခုနှင့် တုံ့ပြန်မှုကိန်းရှင် တစ်ခုတည်းဖြင့်သာ လုပ်ဆောင်နေသောကြောင့် တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုမျဉ်းကို မြင်ယောင်ရန် လွယ်ကူပါသည်။

ဥပမာအားဖြင့်၊ အောက်ပါကုဒ်သည် ဒေတာအတွဲတစ်ခုနှင့် ရိုးရှင်းသော မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုပုံစံကို မည်သို့အံဝင်ခွင်ကျဖြစ်စေရန် ဖော်ပြပြီး ရလဒ်များကို ပုံဖော်နိုင်သည်-

 #create dataset
data <- data.frame(x = c(1, 1, 2, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 11),
                   y = c(13, 14, 17, 23, 24, 25, 25, 24, 28, 32, 33, 35, 40, 41))

#fit simple linear regression model
model <- lm(y ~ x, data = data)

#create scatterplot of data
plot(data$x, data$y)

#add fitted regression line
abline(model)

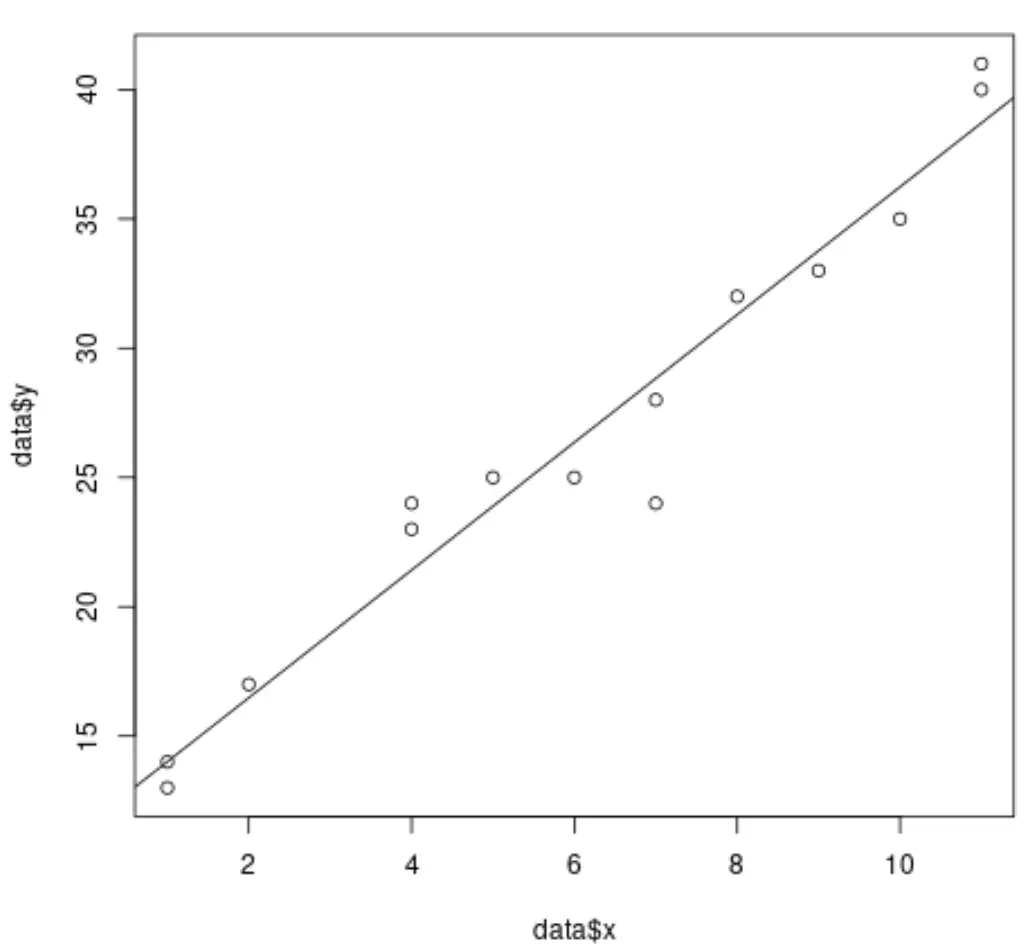
သို့သော်၊ ကျွန်ုပ်တို့သည် မျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှုများစွာကို လုပ်ဆောင်သောအခါ၊ ကြိုတင်ခန့်မှန်းနိုင်သော ကိန်းရှင်များစွာရှိသောကြောင့် ရလဒ်များကို မြင်ယောင်ရန် ခက်ခဲလာပြီး 2D ဂရပ်ပေါ်တွင် ကျွန်ုပ်တို့သည် ဆုတ်ယုတ်မှုမျဉ်းကို ရိုးရှင်းစွာ မကြံစည်နိုင်ပါ။

ယင်းအစား၊ ကျွန်ုပ်တို့သည် ထပ်လောင်း variable plots (တစ်ခါတစ်ရံ “ partial regression plots” ဟုခေါ်သည်) ကိုသုံးနိုင်သည်၊ ၎င်းသည် တုံ့ပြန်မှုကိန်းရှင်နှင့် ခန့်မှန်းသူကိန်းရှင်ကြားရှိ ဆက်နွယ်မှုကိုပြသသည့် တစ်စိတ်တစ်ပိုင်းကွက်ကွက်များ ဖြစ်ပြီး မော်ဒယ်ရှိ အခြားကြိုတင်ခန့်မှန်းသူကိန်းရှင်များရှိနေခြင်းအတွက် ထိန်းချုပ်နေစဉ် ။

အောက်ဖော်ပြပါ ဥပမာသည် R တွင် မျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှု အများအပြားကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသပြီး ပေါင်းစပ်ထည့်သွင်းထားသော ပြောင်းလဲနိုင်သောကွက်များကို အသုံးပြု၍ ရလဒ်များကို မြင်ယောင်ကြည့်ပါ။

ဥပမာ- R တွင် မျဉ်းကြောင်းပြန်ဆုတ်မှုရလဒ်များစွာကို ပုံဖော်ခြင်း။

တပ်ဆင်ထားသော mtcars ဒေတာအစုံကို အသုံးပြု၍ R ရှိ ဒေတာအတွဲတစ်ခုနှင့် ကျွန်ုပ်တို့သည် အောက်ဖော်ပြပါ မျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှုပုံစံမျိုးစုံကို ဖြည့်သွင်းသည်ဆိုပါစို့။

 #fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view results of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-5.1225 -1.8454 -0.4456 1.1342 6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 * 
hp -0.031229 0.013345 -2.340 0.02663 * 
drat 2.714975 1.487366 1.825 0.07863 . 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509 
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09

ရလဒ်များမှ၊ coefficient တစ်ခုစီအတွက် p-value သည် 0.1 ထက်နည်းသည်ကို တွေ့နိုင်ပါသည်။ ရိုးရှင်းစေရန်အတွက်၊ ခန့်မှန်းပေးသည့်ကိန်းရှင်တစ်ခုစီသည် သိသာထင်ရှားပြီး မော်ဒယ်တွင် ထည့်သွင်းသင့်သည်ဟု ကျွန်ုပ်တို့ယူဆပါမည်။

နောက်ဆက်တွဲ variable များ၏ကွက်ကွက်များထုတ်လုပ်ရန်၊ ကျွန်ုပ်တို့သည် ကား ပက်ကေ့ခ်ျမှ avPlots() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်ပါသည်။

 #load car package
library(car)

#produce added variable plots
avPlots(model)

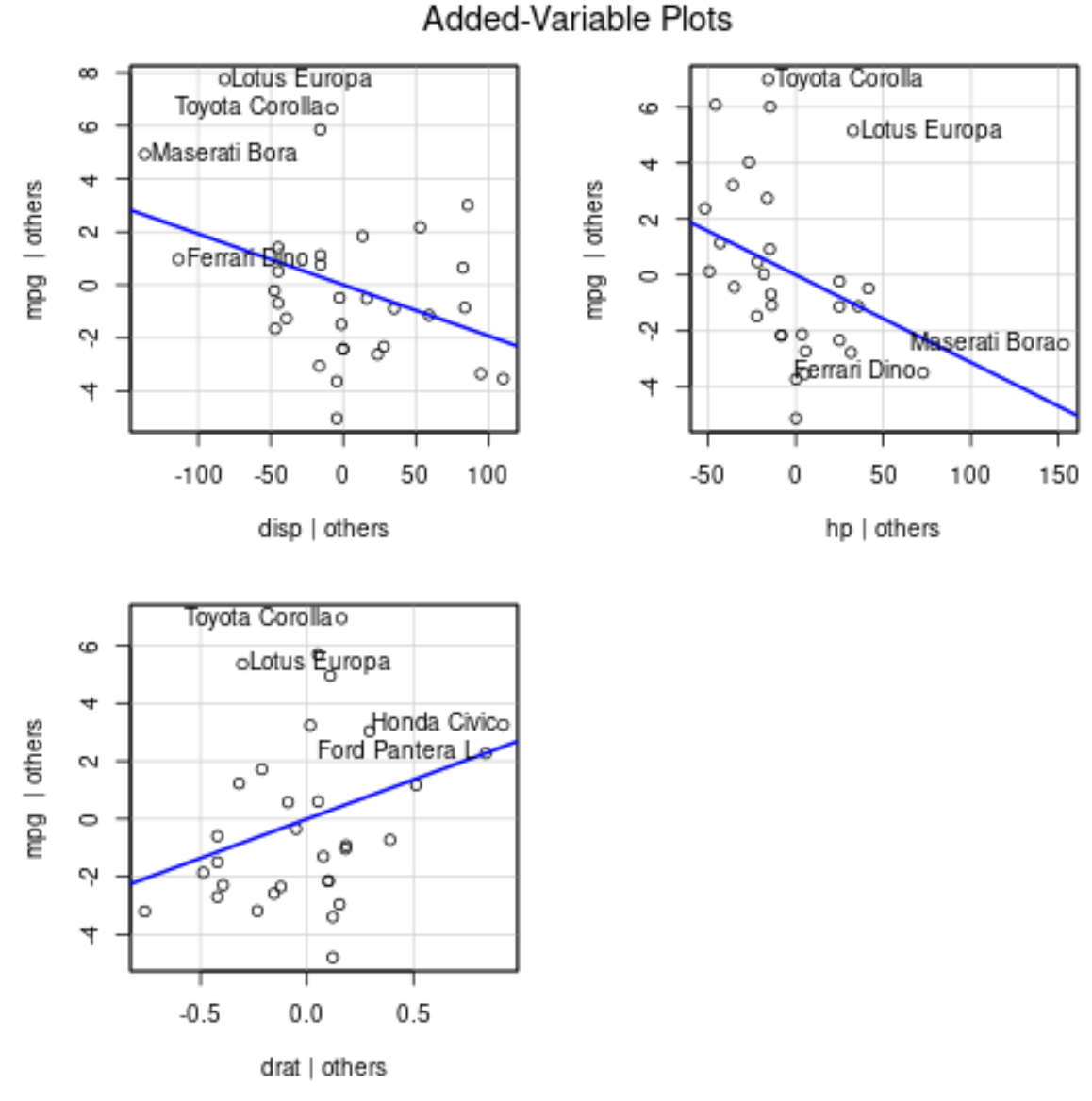
ဤသည်မှာ ဇာတ်ကွက်တစ်ခုစီကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုရမည်နည်း၊

• x-axis သည် တစ်ခုတည်းသော ခန့်မှန်းချက်ကိန်းရှင်ကိုပြသပြီး y-axis သည် တုံ့ပြန်မှုပြောင်းလဲခြင်းကိုပြသသည်။
• အပြာရောင်မျဉ်းသည် ခန့်မှန်းသူကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်ကြား ဆက်စပ်မှုကို ပြသသည်၊၊ အခြားကြိုဟောသူကိန်းရှင်အားလုံး၏ တန်ဖိုးကို ကိန်းသေအဖြစ် ထိန်းထားစဉ် ။
• ဂရပ်တစ်ခုစီရှိ အညွှန်းတပ်ထားသောအချက်များသည် အကြီးဆုံး အကြွင်းအကျန်များ ဖြင့် ရှုမြင်သုံးသပ်ချက် 2 ခုနှင့် အကြီးဆုံးတစ်စိတ်တစ်ပိုင်းလွှမ်းမိုးမှုရှိသော ရှုမြင်သုံးသပ်ချက် 2 ခုကို ကိုယ်စားပြုသည်။

ကွက်တစ်ခုစီရှိ မျဉ်း၏ထောင့်သည် ခန့်မှန်းဆုတ်ယုတ်မှုညီမျှခြင်း၏ ဖော်ကိန်း၏ နိမိတ်လက္ခဏာနှင့် ကိုက်ညီကြောင်း သတိပြုပါ။

ဥပမာအားဖြင့်၊ ဤသည်မှာ မော်ဒယ်ရှိ ခန့်မှန်းသူ ကိန်းရှင်တစ်ခုစီအတွက် ခန့်မှန်းကိန်းများဖြစ်သည်-

• ပြသမှု- -0.019232
• ch: -0.031229
• ရက်စွဲ- 2.714975

disp နှင့် hp တို့အတွက် အနုတ်လက္ခဏာဖြစ်နေသော်လည်း၊ ၎င်းတို့၏ ခန့်မှန်းချက်ကိန်းဂဏန်းများ၏ နိမိတ်လက္ခဏာများနှင့် ကိုက်ညီသည့် drat အတွက် ထပ်ထည့်သော variable plot တွင် မျဉ်း၏ထောင့်သည် အပြုသဘောဖြစ်ကြောင်း သတိပြုပါ။

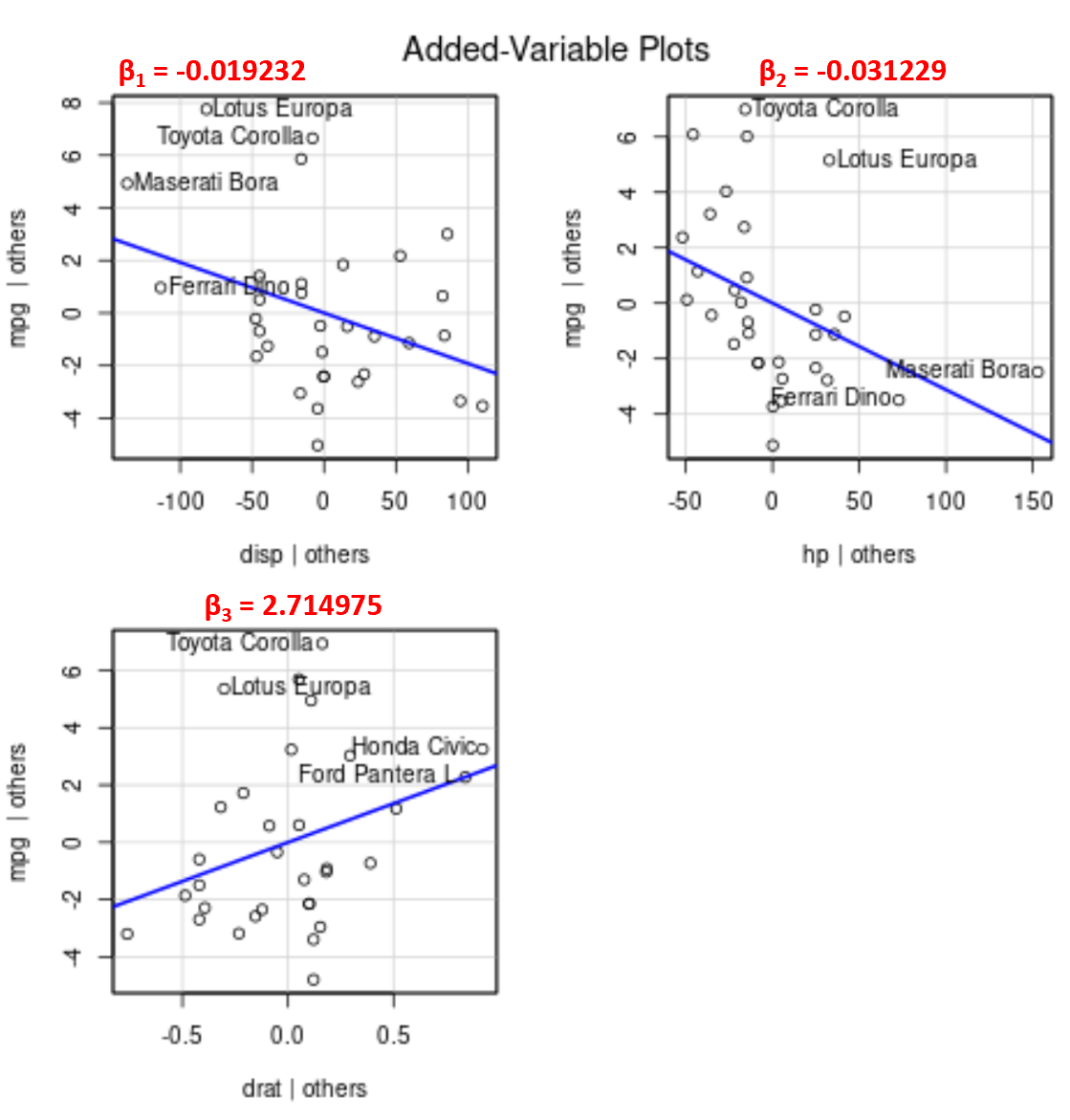
ကျွန်ုပ်တို့တွင် ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်များစွာရှိသောကြောင့် 2D ဂရပ်တစ်ခုတွင် တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုမျဉ်းတစ်ကြောင်းကို ကျွန်ုပ်တို့မဆွဲနိုင်သော်လည်း၊ ဤထည့်သွင်းထားသောကိန်းရှင်ဂရပ်များသည် ကျွန်ုပ်တို့အား အခြားခန့်မှန်းကိန်းရှင်ကိန်းရှင်တစ်ခုစီနှင့် တုံ့ပြန်မှုကိန်းရှင်တို့ကြား ဆက်နွယ်မှုကို စောင့်ကြည့်လေ့လာနိုင်စေပါသည်။