ကိန်းရှင်များကြား လိုင်းမဟုတ်သော ဆက်ဆံရေး၏ ဥပမာ 5 ခု

စာရင်းအင်းသင်တန်းအများစုတွင်၊ ကျောင်းသားများသည် ကိန်းရှင်များကြား မျဉ်းသားသော ဆက်ဆံရေးများအကြောင်း လေ့လာကြသည်။

ဤအရာများသည် ကိန်းရှင်တစ်ခုတွင် တိုးလာခြင်းနှင့် အခြားကိန်းရှင်တစ်ခုတွင် ခန့်မှန်းနိုင်သော တိုးလာခြင်းနှင့် ဆက်စပ်နေသည့် ဆက်ဆံရေးများဖြစ်သည်။

ဤဥပမာတစ်ခုသည် ဘတ်စကက်ဘောဂိမ်းတွင် ကစားသည့် မိနစ်အရေအတွက် ဖြစ်နိုင်သည်-

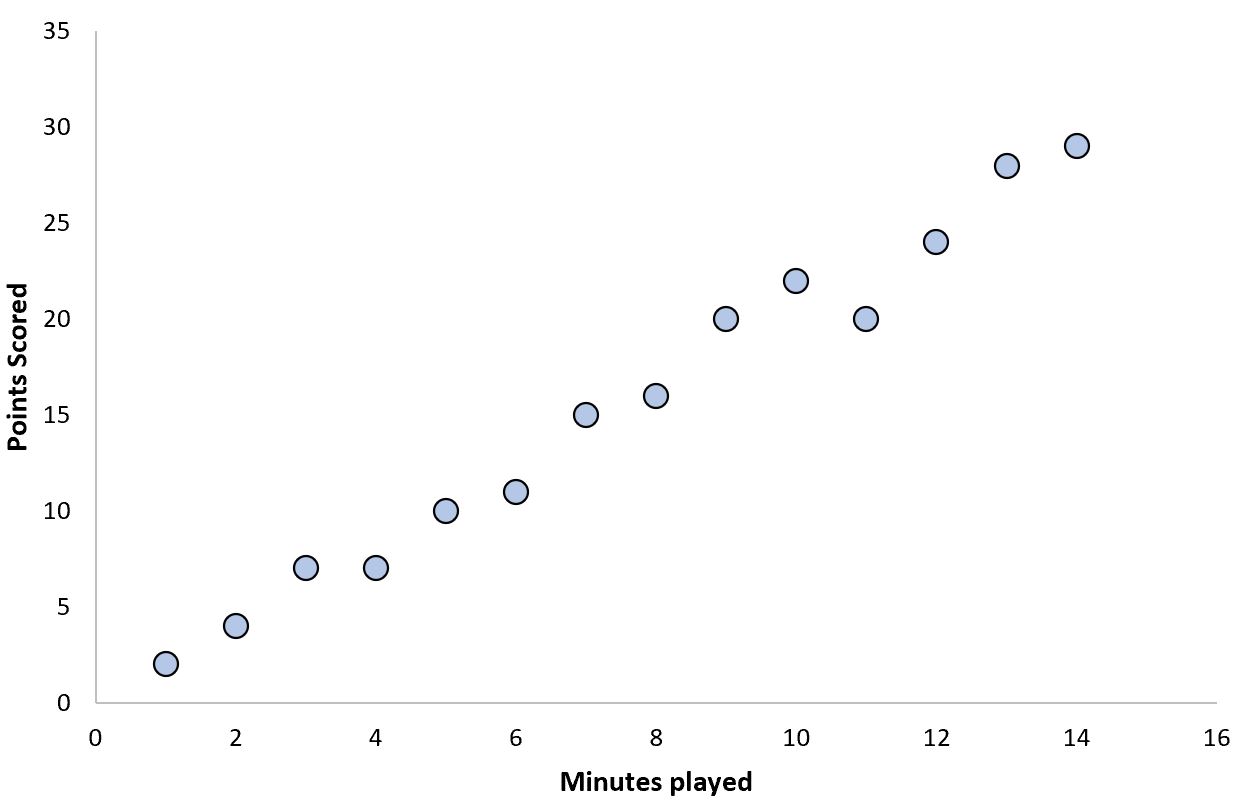
မိနစ်ပိုကစားသူများသည် အမှတ်ပိုရတတ်သည်။

သို့သော်လည်း၊ ကိန်းရှင်များကြားတွင် လိုင်းမဟုတ်သော ဆက်ဆံရေး များလည်း ရှိနိုင်ပြီး ၎င်းတို့သည် လက်တွေ့ကမ္ဘာတွင် အဆက်မပြတ် မြင်တွေ့နေရပါသည်။

ဤသင်ခန်းစာသည် လက်တွေ့ကမ္ဘာရှိ ကိန်းရှင်များကြား လိုင်းမဟုတ်သော ဆက်ဆံရေး နမူနာငါးခုကို ပေးသည်။

ဥပမာ 1- လေးထောင့်ပုံ ဆက်ဆံရေး

လက်တွေ့ကမ္ဘာတွင် အသုံးအများဆုံး လိုင်းမဟုတ်သော ဆက်ဆံရေးများထဲမှ တစ်ခုသည် ကိန်းရှင်များကြားတွင် လေးပုံတစ်ပုံ ဆက်ဆံရေး ဖြစ်သည်။

ခွဲခြမ်းစိပ်ဖြာမှုတစ်ခုတွင် ပုံဖော်သည့်အခါ၊ ဤဆက်ဆံရေးသည် ပုံမှန်အားဖြင့် “ U” ပုံသဏ္ဍာန်ရှိသည်။

ဥပမာတစ်ခုသည် အလုံးစုံပျော်ရွှင်မှုနှင့် နှိုင်းယှဉ်ပါက တစ်ပတ်လျှင် စုစုပေါင်းအလုပ်ချိန် ဖြစ်နိုင်သည်-

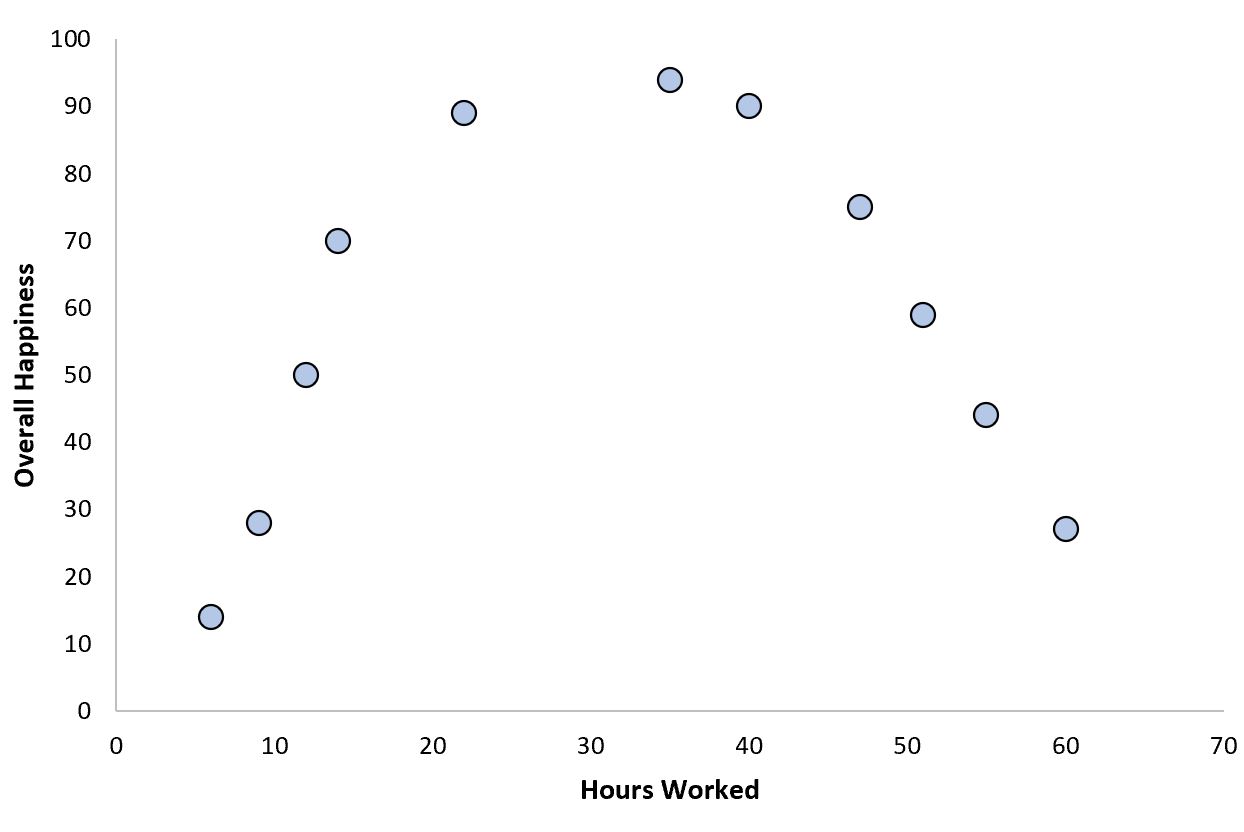
အလုပ်ချိန် သုညမှ တိုးလာသည်နှင့်အမျှ ပျော်ရွှင်မှု အလုံးစုံ တိုးလာတတ်သည်၊ သို့သော် သတ်မှတ်ထားသော သတ်မှတ်ချက်ထက် ကျော်လွန်ကာ အလုပ်ချိန်များ ပိုများလာခြင်းသည် အမှန်တကယ် ပျော်ရွှင်မှု လျော့ကျသွားစေသည်။

ပြောင်းပြန်ပြောင်းထားသော ဤ “ U” ပုံသဏ္ဍာန်သည် ကိန်းရှင်နှစ်ခုကြားရှိ လေးထောင့်ပုံသဏ္ဍာန် ဆက်ဆံရေးပုံစံဖြစ်သည်။

ဥပမာ 2- Cubic ဆက်ဆံရေး

လက်တွေ့ကမ္ဘာတွင် အဖြစ်များသော အခြားလိုင်းမဟုတ်သော ဆက်ဆံရေးသည် ကိန်းရှင်များကြား ကုဗိပ်ဆက်နွယ်မှု ဖြစ်သည်။

ခွဲခြမ်းစိပ်ဖြာမှုတစ်ခုတွင် ပုံဖော်သည့်အခါ၊ ဤဆက်ဆံရေးသည် ပုံမှန်အားဖြင့် ကွဲပြားသောမျဉ်းကွေးနှစ်ခုကို ပြသသည်။

ဤဆက်ဆံရေးအမျိုးအစားသည် သာမိုဒိုင်းနမစ်နယ်ပယ်ရှိ ကိန်းရှင်များကြားတွင် မကြာခဏတည်ရှိသည်-

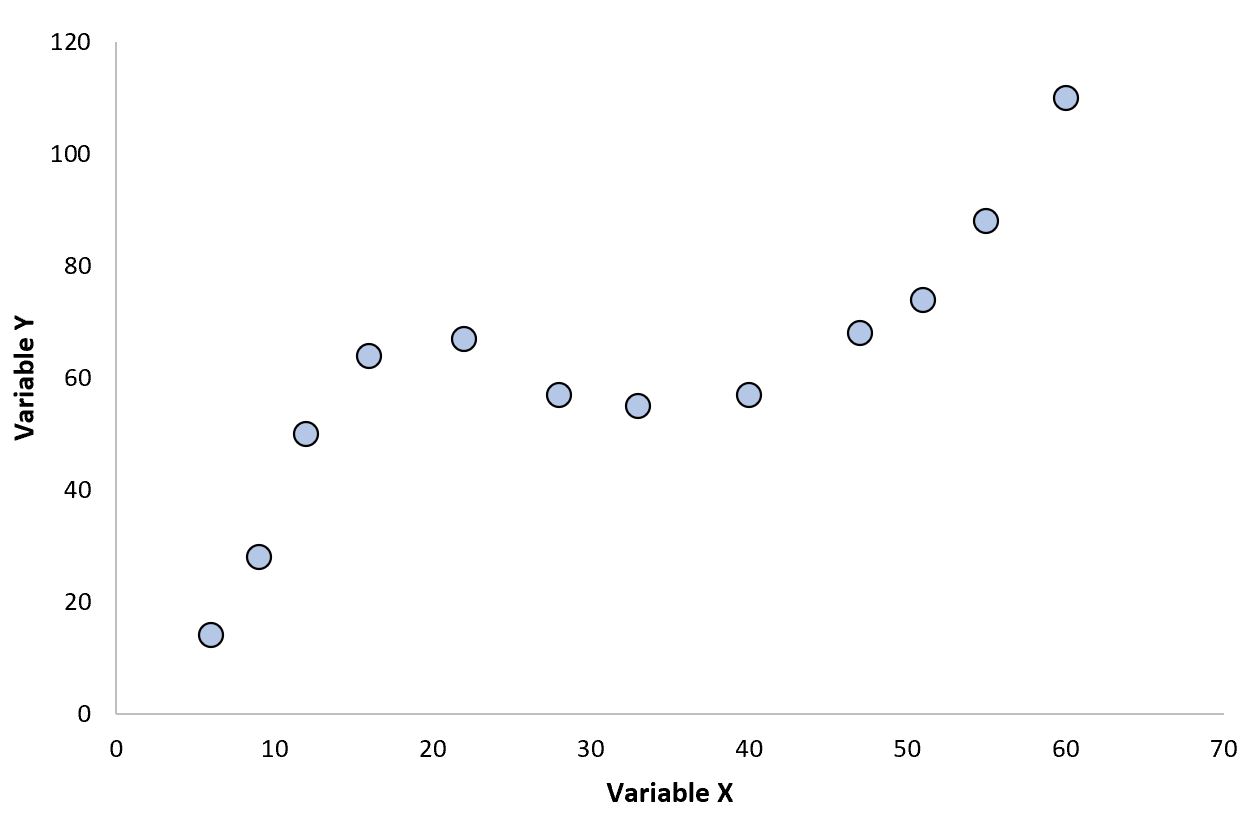
ကွက်ကွက်တွင် ကွဲပြားသောမျဉ်းကွေးနှစ်ခုရှိပြီး ကိန်းရှင် X နှင့် ကိန်းရှင် Y အကြား ဆက်နွယ်မှုသည် မျဉ်းဖြောင့်မဟုတ်ကြောင်း သတိပြုပါ။

ဥပမာ 3- Exponential ဆက်ဆံရေး

လက်တွေ့ကမ္ဘာတွင် အဖြစ်များသော လိုင်းမဟုတ်သော ဆက်ဆံရေး နောက်တစ်ခုမှာ ကိန်းရှင်များကြားတွင် ထပ်ကိန်းထုတ်သည့် ဆက်ဆံရေး ဖြစ်သည်။

scatterplot တစ်ခုပေါ်တွင် ကြံစည်သောအခါ၊ ဤဆက်နွယ်မှုသည် x-axis ပေါ်ရှိ variable တိုးလာသည်နှင့်အမျှ ပိုမိုသိသာထင်ရှားလာမည့် ထူးခြားသောမျဉ်းကွေးတစ်ခုကို ပြသသည်။

ကိန်းဂဏန်းဆက်စပ်မှု၏ လူသိများသော ဥပမာတစ်ခုမှာ ဝါးပင်များ၏ သက်တမ်းနှင့် ၎င်းတို့၏ နှစ်စဉ်ကြီးထွားမှုဖြစ်သည်။

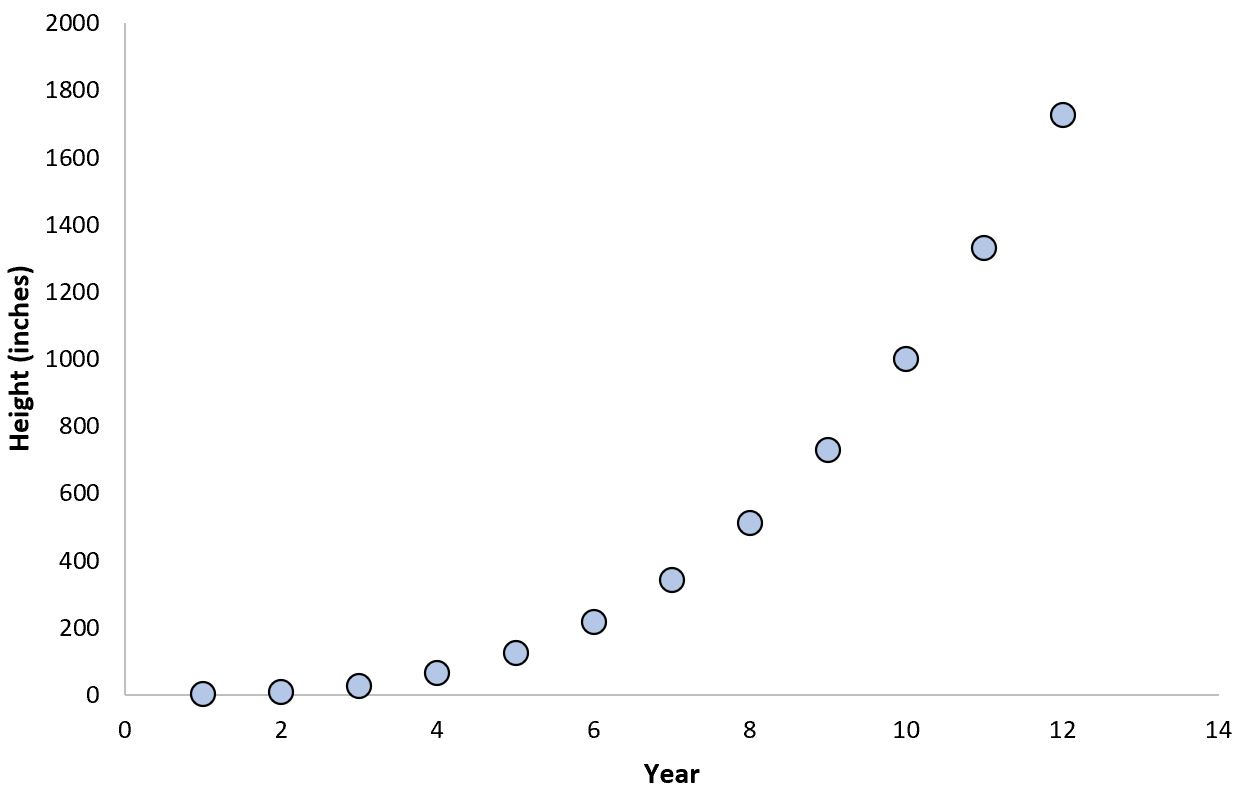
ကြီးထွားမှု ပထမနှစ်အနည်းငယ်အတွင်း ဝါးပင်သည် အလွန်နှေးကွေးစွာ ကြီးထွားလာသော်လည်း သတ်မှတ်ထားသော အသက်အရွယ်ရောက်သည်နှင့် အမြင့်တွင် ပေါက်ကွဲပြီး လျင်မြန်စွာ ကြီးထွားလာသည်။

ဥပမာ 4- လော့ဂရစ်သမ် ဆက်ဆံရေး

လက်တွေ့ကမ္ဘာတွင် အသုံးများသည့် လိုင်းမဟုတ်သော ဆက်ဆံရေးနောက်ထပ်တစ်ခုမှာ ကိန်းရှင်များကြားရှိ လော့ဂရစ်သမ် ဆက်ဆံရေး ဖြစ်သည်။

scatterplot တစ်ခုပေါ်တွင် ကြံစည်သောအခါ၊ ဤဆက်နွယ်မှုသည် x-axis ပေါ်ရှိ variable တိုးလာသည်နှင့်အမျှ အသံထွက်နည်းသွားသည့် ထူးခြားသောမျဉ်းကွေးတစ်ခုကို ပြသသည်။

လော့ဂရစ်သမ်ဆက်နွယ်မှု၏ ဥပမာတစ်ခုမှာ စမတ်အိမ်သုံးနည်းပညာများ၏ ထိရောက်မှုနှင့် အချိန်အကြားဖြစ်သည်-

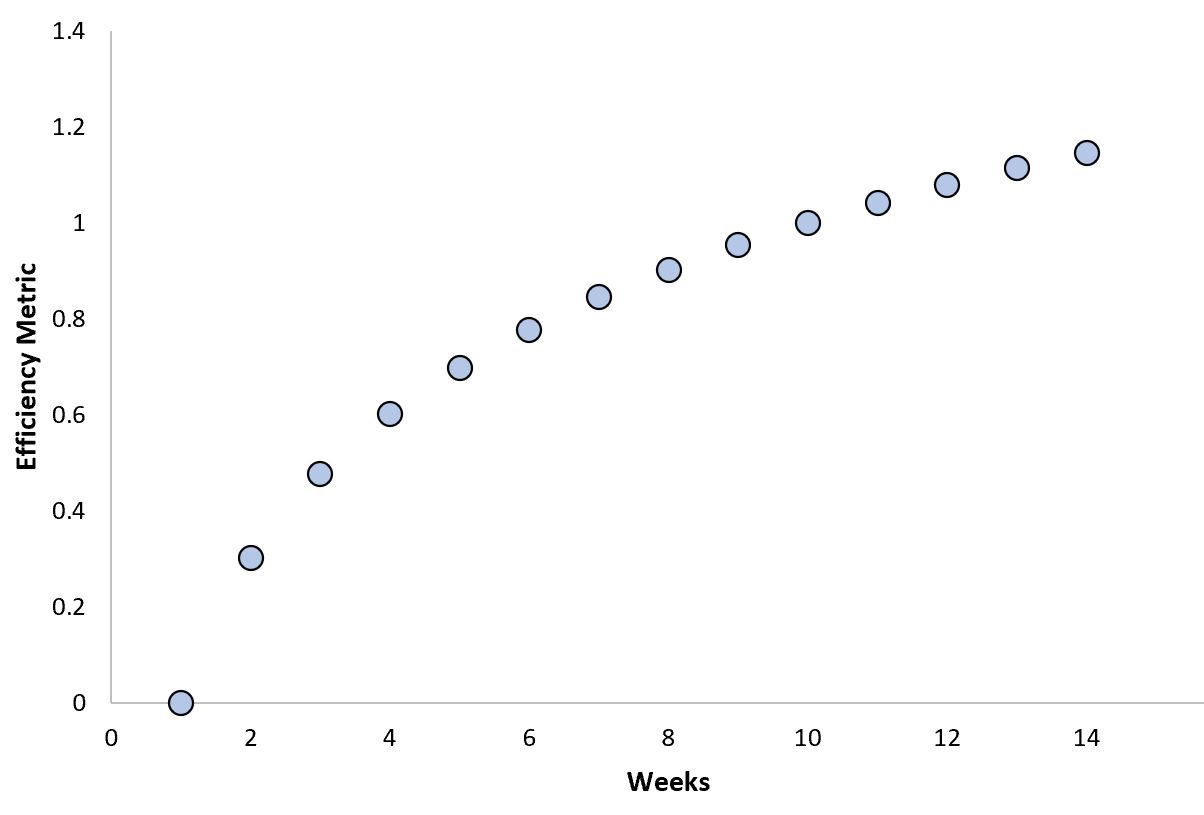
စမတ်အိမ်နည်းပညာအသစ် (ဖုန်စုပ်စက် သို့မဟုတ် သီးသန့်လေအေးပေးစက်ကဲ့သို့) အိမ်တွင် တပ်ဆင်သောအခါ၊ ၎င်းသည် မည်ကဲ့သို့ ပိုမိုထိရောက်မည်ကို လျင်မြန်စွာ သိရှိနိုင်သော်လည်း အချို့နေရာသို့ရောက်သည်နှင့် ၎င်းသည် အမြင့်ဆုံးအဆင့်သို့ ရောက်ရှိသွားပါသည်။

ဥပမာ 5- Cosine ဆက်ဆံရေး

လက်တွေ့ကမ္ဘာတွင် အဖြစ်များသော အခြားလိုင်းမဟုတ်သော ဆက်ဆံရေးသည် ကိန်းရှင်များကြားတွင် ကို ဆိုက်ဆက်နွယ်မှု ဖြစ်သည်။

ကွက်ကျားကွက်ကွက်တစ်ခုကို ပုံဖော်သောအခါ၊ ဤဆက်ဆံရေးသည် “ လှိုင်း” ပုံသဏ္ဍာန်ရှိသည်။

cosine ဆက်နွယ်မှု၏ ဥပမာတစ်ခုမှာ အသံလှိုင်းများ၏ ကြိမ်နှုန်းနှင့် အချိန်တို့ကြားတွင်၊

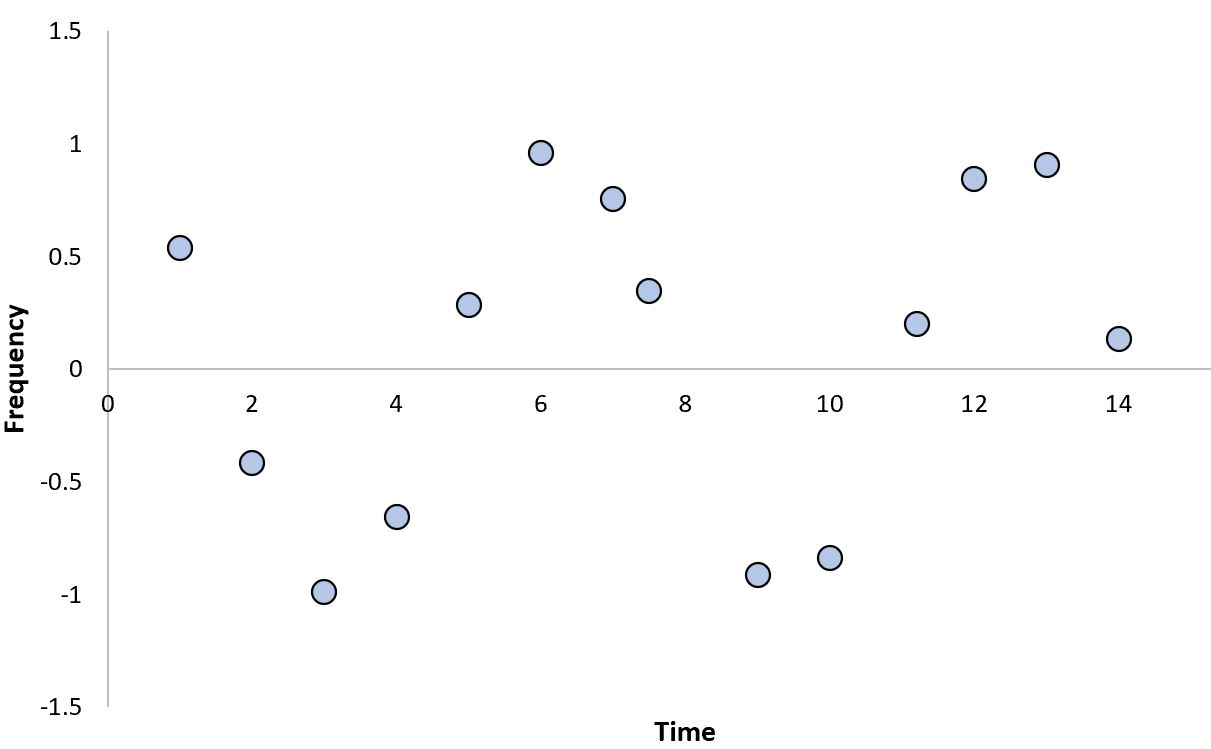
ဆက်ဆံရေးတွင် အလွန်လိုင်းမဆန်သော “လှိုင်း” ပုံသဏ္ဍာန်ရှိပုံကို သတိပြုပါ။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် Excel တွင် linear မဟုတ်သော ဆုတ်ယုတ်မှု အမျိုးအစားများကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

Excel တွင် လေးပုံတပုံ ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်နည်း
Excel တွင် cubic regression လုပ်ဆောင်နည်း
Excel တွင် Exponential Regression လုပ်ဆောင်နည်း
Excel တွင် logarithmic regression ကိုမည်သို့လုပ်ဆောင်ရမည်နည်း