ထူးထူးခြားခြား အချိုးတွေကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။

စာရင်းဇယားများတွင်၊ ဖြစ်နိုင်ခြေသည် ဖြစ်ရပ်တစ်ခု ဖြစ်ပွားနိုင်ခြေကို ရည်ညွှန်းသည်။ အောက်ပါအတိုင်း တွက်ချက်သည်။

ဖြစ်နိုင်ခြေ-

P(ဖြစ်ရပ်) = (#နှစ်လိုဖွယ်ရလဒ်များ) / (ဖြစ်နိုင်သောရလဒ်များ #)

ဥပမာ၊ အိတ်တစ်လုံးမှာ အနီရောင်ဘောလုံးလေးလုံးနဲ့ အစိမ်းရောင်ဘောလုံးတစ်လုံးရှိတယ်ဆိုပါစို့။ မျက်စိမှိတ်ပြီး ကျပန်းရွေးချယ်ပါက အစိမ်းရောင်ဘောလုံးကို သင်ရွေးချယ်သည့် ဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်ပါသည်။

P(အစိမ်းရောင်) = 1/5 = 0.2 ။

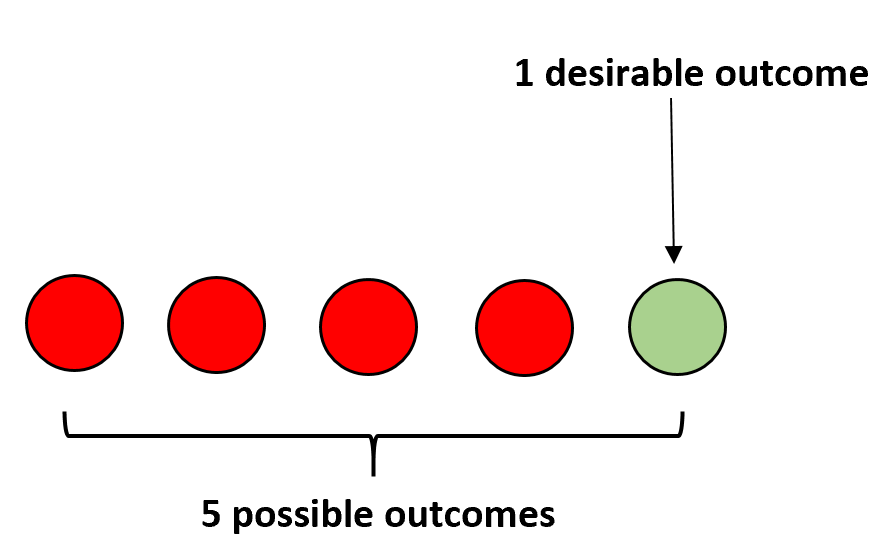
အဖြစ်အပျက်တစ်ခု ဖြစ်ပွားနိုင် ခြေကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

ODDS-

အခွင့်အလမ်းများ (ဖြစ်ရပ်) = P (ဖြစ်ရပ်ဖြစ်ပွားသည်) / 1-P (ဖြစ်ရပ်ဖြစ်ပေါ်မှု)၊

ဥပမာအားဖြင့်၊ အစိမ်းရောင်ဘောလုံးကို ပစ်ခတ်နိုင်မှုနှုန်းများမှာ (0.2)/1-(0.2) = 0.2/0.8 = 0.25 ဖြစ်သည်။

odds ratio သည် ဖြစ်နိုင်ခြေ နှစ်ခု၏ အချိုးဖြစ်သည်။

ကံကောင်းခြင်းအစီရင်ခံစာ-

Odds Ratio = ဖြစ်ရပ်များ၏ မရေမတွက်နိုင်သော A/ Odds of Event B

ဥပမာအားဖြင့်၊ အနီရောင်ဘောလုံးနှင့် အစိမ်းရောင်ဘောလုံးကို ရွေးချယ်ခြင်းကြားတွင် လေးနက်မှုအချိုးကို တွက်ချက်နိုင်သည်။

အနီရောင်ဘောလုံးကိုဆွဲရန်ဖြစ်နိုင်ခြေမှာ 4/5 = 0.8 ဖြစ်သည်။

အနီရောင်ဘောလုံးဆွဲရန်အခွင့်အရေးများမှာ (0.8) / 1-(0.8) = 0.8 / 0.2 = 4 ဖြစ်သည်။

အစိမ်းရောင်ဘောလုံးတစ်ခုပေါ်ရှိ အနီရောင်ဘောလုံးကို ရွေးချယ်ရန်အတွက် ပေါက်ကြားမှုအချိုး ကို အောက်ပါအတိုင်း တွက်ချက်ပါသည်။

Odds (အနီရောင်) / Odds (အစိမ်းရောင်) = 4 / 0.25 = 16 ။

ဒါကြောင့် အနီရောင်ဘောလုံးကို ပစ်ခတ်နိုင်တဲ့အခွင့်အရေးက အစိမ်းရောင်ဘောလုံးကို ပစ်ခတ်နိုင်တဲ့အခွင့်အရေးထက် 16 ဆ ပိုများပါတယ်။

လက်တွေ့ကမ္ဘာတွင် ထူးထူးခြားခြား အချိုးများကို မည်သည့်အချိန်တွင် အသုံးပြုကြသနည်း။

လက်တွေ့ကမ္ဘာတွင်၊ သုတေသီများ ဖြစ်ပျက်နေသည့် အဖြစ်အပျက်နှစ်ခု၏ မသာမယာများကို နှိုင်းယှဉ်လိုသည့် အခြေအနေအမျိုးမျိုးတွင် ထူးထူးခြားခြား အချိုးများကို အသုံးပြုပါသည်။ ဤသည်မှာ ဥပမာအချို့ဖြစ်သည်။

ဥပမာ # 1- ထူးထူးခြားခြား အချိုးများကို ဘာသာပြန်ခြင်း။

ကုသမှုအသစ်တစ်ခုသည် လက်ရှိကုသမှုနှင့် နှိုင်းယှဉ်ပါက အပြုသဘောဆောင်သောကျန်းမာရေးရလဒ်ကို လူနာတစ်ဦးခံစားရနိုင်ခြေကို ပိုမိုကောင်းမွန်စေကြောင်း သုတေသီများက သိချင်ကြသည်။ အောက်ပါဇယားသည် ကုသမှုအပေါ် မူတည်၍ အပေါင်းလက္ခဏာ သို့မဟုတ် အနုတ်လက္ခဏာ ကျန်းမာရေးရလဒ်ကို ခံစားရသော လူနာအရေအတွက်ကို ပြသထားသည်။

ကုသမှုအသစ်ဖြင့် အပြုသဘောဆောင်သောရလဒ်ကို ခံစားရသော လူနာတစ်ဦး၏ အခွင့်အလမ်းများကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

အခွင့်အလမ်းများ = P(အပြုသဘော) / 1 – P(အပြုသဘော) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1.25

ရှိပြီးသားကုသမှုဖြင့် အပြုသဘောဆောင်သောရလဒ်ကို ခံစားရသော လူနာတစ်ဦး၏ အခွင့်အလမ်းများကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

အခွင့်အလမ်းများ = P(positive) / 1 – P(positive) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0.875

ထို့ကြောင့် လက်ရှိကုသမှုနှင့် နှိုင်းယှဉ်ပါက ကုသမှုအသစ်ဖြင့် အပြုသဘောဆောင်သောရလဒ်ရရှိခြင်း၏ မသာမညအချိုးကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

အတိုးနှုန်းအချိုး = 1.25 / 0.875 = 1.428 ။

ကုသမှုအသစ်ကို အသုံးပြုသည့် လူနာတစ်ဦး၏ အပြုသဘောဆောင်သော ရလဒ်ရရှိရန် အခွင့်အလမ်းများသည် ရှိပြီးသားကုသမှုကို အသုံးပြု၍ လူနာတစ်ဦး၏ အပြုသဘောဆောင်သော ရလဒ်ရရှိခြင်း၏ အ ခွင့်အလမ်းများ ထက် 1.428 ဆ ရှိသည်ဟု ဆိုလိုခြင်းဖြစ်သည်။

တစ်နည်းဆိုရသော် ကုသမှုအသစ်ဖြင့် အပြုသဘောဆောင်သောရလဒ်ကို တွေ့ကြုံခံစားနိုင်ခြေ 42.8% တိုးလာသည်။

ဥပမာ #2- ထူးထူးခြားခြား အချိုးများကို ဘာသာပြန်ခြင်း။

ကြော်ငြာတစ်ခုသည် သုံးစွဲသူများအား အခြားကြော်ငြာတစ်ခုထက် ပေးထားသည့်အရာတစ်ခုကို မကြာခဏဝယ်ယူစေခြင်း ရှိ၊မရှိ စျေးကွက်ရှာဖွေသူများသည် သိချင်ကြသည်။ ဒါကြောင့် သူတို့က ကြော်ငြာတစ်ခုစီကို လူ 100 ကိုပြတယ်။ အောက်ဖော်ပြပါဇယားတွင် ၎င်းတို့မြင်ရသည့်ကြော်ငြာအပေါ်အခြေခံ၍ ပစ္စည်းဝယ်ယူသူအရေအတွက်ကို ပြသသည်-

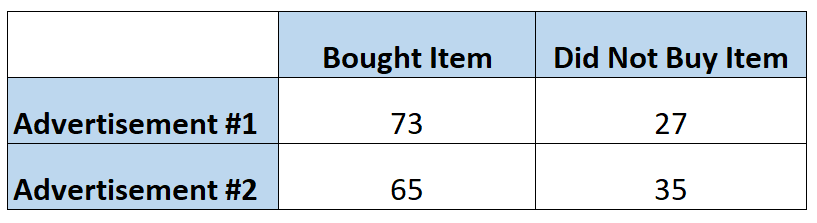
ပထမဆုံးကြော်ငြာကိုမြင်ပြီးနောက် ပစ္စည်းဝယ်ယူသည့်လူတစ်ဦး၏ အခွင့်အလမ်းများကို အောက်ပါအတိုင်း တွက်ချက်နိုင်သည်-

အတိုးနှုန်း = P(ဝယ်) / 1 – P(ဝယ်) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2.704

ဒုတိယကြော်ငြာကိုမြင်ပြီးနောက် ပစ္စည်းကိုဝယ်ယူသူ တစ်ဦးချင်းစီ၏ အခွင့်အလမ်းများကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

အတိုးနှုန်း = P(ဝယ်) / 1 – P(ဝယ်) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1.857

ထို့ကြောင့် ပထမကြော်ငြာကိုမြင်ပြီးနောက် ပစ္စည်းဝယ်ယူသည့်ဖောက်သည်တစ်ဦးနှင့် ဒုတိယကြော်ငြာကိုတွေ့ပြီးနောက် ဝယ်ယူမှုနှင့် ကုန်ပစ္စည်းဝယ်ယူမှုအတွက် လေးနက်မှုအချိုးကို အောက်ပါအတိုင်း တွက်ချက်နိုင်သည်-

အတိုးနှုန်းအချိုး = 2.704 / 1.857 = 1.456 ။

ပထမကြော်ငြာကိုမြင်ပြီးနောက် ပစ္စည်းဝယ်ယူသူ တစ်ဦးချင်းစီ၏ မသာမယာများသည် ဒုတိယကြော်ငြာကိုမြင်ပြီးနောက် ကုန်ပစ္စည်းဝယ်ယူသူ တစ်ဦးချင်းစီ၏ မသာမ ယာ ထက် 1.456 ဆ ဟု ဆိုလိုခြင်းဖြစ်သည်။

တစ်နည်းဆိုရသော် ပထမစာရင်းကြောင့် ပစ္စည်းဝယ်ယူရန် အခွင့်အလမ်း 45.6% တိုးလာသည်။

ထပ်လောင်းအရင်းအမြစ်များ

Excel တွင် Odds Ratio နှင့် Relative Risk တွက်ချက်နည်း
1 ထက်နည်းသော odds အချိုးကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံ
နှိုင်းရအန္တရာယ်ကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။