တစ်လမ်းသွား anova- အဓိပ္ပါယ်၊ ဖော်မြူလာနှင့် ဥပမာ
တစ်လမ်းသွား ANOVA (“ ကွဲလွဲမှုကို ခွဲခြမ်းစိတ်ဖြာခြင်း” ) သည် သက်ဆိုင်ရာလူဦးရေ၏နည်းလမ်းများကြားတွင် စာရင်းအင်းအရ သိသာထင်ရှားသော ခြားနားချက်ရှိမရှိ ဆုံးဖြတ်ရန် သီးခြားလွတ်လပ်သော အုပ်စုသုံးစု သို့မဟုတ် ထို့ထက်ပိုသော နည်းလမ်းများကို နှိုင်းယှဉ်ပါသည်။
ဤသင်ခန်းစာတွင် အောက်ပါတို့ကို ရှင်းပြထားသည်။
- တစ်ကြောင်း ANOVA လုပ်ဆောင်ရန် စေ့ဆော်မှု။
- တစ်ကြောင်း ANOVA လုပ်ဆောင်ရန် ကိုက်ညီရမည့် ယူဆချက်များ။
- တစ်လမ်းမောင်း ANOVA ဖျော်ဖြေရေး လုပ်ငန်းစဉ်။
- တစ်လမ်းမောင်း ANOVA လုပ်ဆောင်ပုံ ဥပမာ။
တစ်လမ်းမောင်း ANOVA- လှုံ့ဆော်မှု
မတူညီသော စာမေးပွဲပြင်ဆင်မှု ပရိုဂရမ်သုံးခုသည် ကောလိပ်ဝင်ခွင့်စာမေးပွဲတွင် မတူညီသော ပျမ်းမျှရမှတ်များ ဖြစ်ပေါ်စေခြင်း ရှိ၊မရှိ သိချင်သည်ဆိုပါစို့။ နိုင်ငံတစ်ဝှမ်းတွင် အထက်တန်းကျောင်းသူ သန်းနှင့်ချီ၍ ရှိနေသောကြောင့် ကျောင်းသားတိုင်းထံ လှည့်ပတ်ပြီး စာမေးပွဲပြင်ဆင်မှု ပရိုဂရမ်များထဲမှ တစ်ခုကို အသုံးပြုခွင့်ပေးရန် အချိန်ကုန်ပြီး စျေးကြီးသည်။
ယင်းအစား၊ ကျွန်ုပ်တို့သည် လူဦးရေ ၁၀၀ ၏ ကျပန်းနမူနာ သုံးခုကို ရွေးချယ်နိုင်ပြီး နမူနာတစ်ခုစီကို စာမေးပွဲအတွက် ပြင်ဆင်ရန် စာမေးပွဲပြင်ဆင်မှု ပရိုဂရမ်သုံးခုအနက်မှ တစ်ခုကို အသုံးပြုခွင့်ပြုပါသည်။ ထို့နောက် ကျောင်းသားတစ်ဦးစီ၏ ရမှတ်များကို စာမေးပွဲဖြေဆိုပြီးသည်နှင့် မှတ်တမ်းတင်နိုင်မည်ဖြစ်သည်။
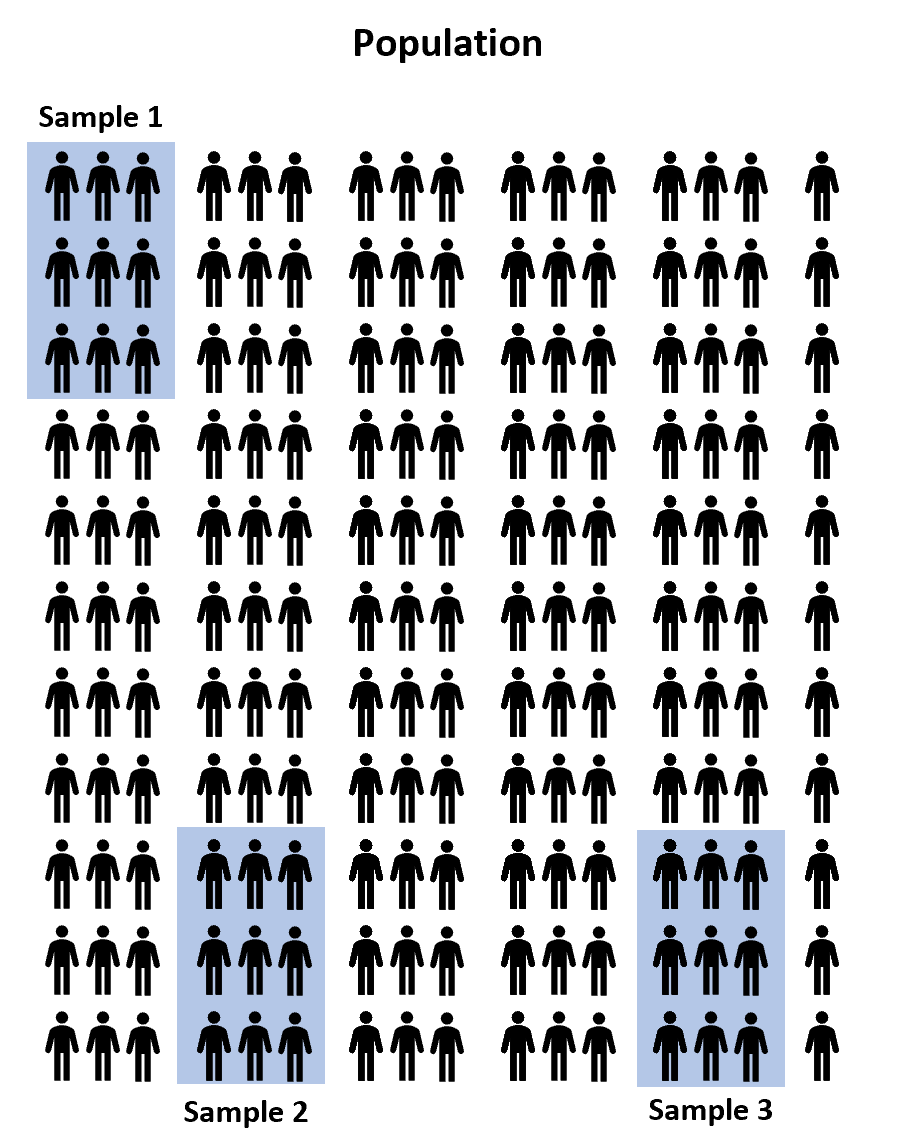
သို့သော် နမူနာသုံးခုကြားရှိ ပျမ်းမျှ စာမေးပွဲရမှတ်သည် အနည်းဆုံး အနည်းငယ်ကွာခြားမည်ဟု အာမခံပါသည်။ မေးခွန်းက ဒီကွာခြားချက်က ကိန်းဂဏန်းအရ သိသာထင်ရှားသလား ။ ကံကောင်းထောက်မစွာ၊ တစ်လမ်းသွား ANOVA သည် ကျွန်ုပ်တို့အား ဤမေးခွန်းကို ဖြေနိုင်စေပါသည်။
တစ်လမ်းမောင်း ANOVA- ယူဆချက်
တစ်လမ်းမောင်း ANOVA ၏ ရလဒ်များ မှန်ကန်စေရန်အတွက်၊ အောက်ပါ ယူဆချက်များနှင့် ကိုက်ညီရမည်-
1. Normality – နမူနာတစ်ခုစီကို ပုံမှန်ဖြန့်ဝေထားသော လူဦးရေမှ ထုတ်ယူထားပါသည်။
2. သာတူညီမျှကွဲလွဲမှုများ – နမူနာများထုတ်ယူသည့် လူဦးရေ၏ကွဲလွဲမှုများသည် တူညီသည်။ ဤယူဆချက်အား စမ်းသပ်ရန် Bartlett’s test ကို အသုံးပြုနိုင်ပါသည်။
3. လွတ်လပ်ရေး – အဖွဲ့တစ်ခုစီမှ လေ့လာတွေ့ရှိချက်များသည် တစ်ခုနှင့်တစ်ခု အမှီအခိုကင်းပြီး အဖွဲ့များအတွင်းမှ လေ့လာချက်များကို ကျပန်းနမူနာဖြင့် ရယူခဲ့ပါသည်။
ဤယူဆချက်များကို မည်သို့အတည်ပြုရမည်ကို အသေးစိတ်သိရှိရန် ဤဆောင်းပါးကို ဖတ်ရှုပါ။
One-way ANOVA: လုပ်ငန်းစဉ်
တစ်လမ်းသွား ANOVA သည် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြုသည်-
- H 0 ( null hypothesis ) : μ 1 = μ 2 = μ 3 = … = μ k (လူဦးရေအားလုံးသည် တူညီသည်)
- H 1 (အခြားသောယူဆချက်)- အနည်းဆုံး လူဦးရေတစ်ခုသည် ကွဲပြားသည်။ အနားယူပါ။
သင်ကိုယ်တိုင်လုပ်ဆောင်ရန် ပျင်းသောကြောင့် တစ်ကြောင်း ANOVA လုပ်ဆောင်ရန် သင်ပုံမှန်အားဖြင့် အချို့သော စာရင်းအင်းဆော့ဖ်ဝဲများ (ဥပမာ R၊ Excel၊ Stata၊ SPSS စသည်ဖြင့်) ကို အသုံးပြုပါမည်။
သင်အသုံးပြုသည့်ဆော့ဖ်ဝဲလ်ကို မည်သို့ပင်ဖြစ်စေ၊ သင်သည် အောက်ပါဇယားကို output အဖြစ် လက်ခံရရှိလိမ့်မည်-
| အရင်းအမြစ် | စတုရန်းများပေါင်း (SS) | df | ပျမ်းမျှစတုရန်းများ (MS) | F | p |
|---|---|---|---|---|---|
| ကုသမှု | RSS | df r | MSR | MSR/MSE | F df r , df e |
| အမှား | ESS | df e | MSE | ||
| စုစုပေါင်း | OHS | df t |
ရွှေ-
- SSR- နှစ်ထပ်ဆုတ်ယုတ်မှု၏ ပေါင်းလဒ်
- SSE- နှစ်ထပ်ကိန်းအမှား၏ပေါင်းလဒ်
- SST- စုစုပေါင်းစတုရန်းများ (SST = SSR + SSE)
- df r : လွတ်လပ်မှု ဆုတ်ယုတ်မှုဒီဂရီ (df r = k-1)
- df e : လွတ်လပ်မှု အမှားဒီဂရီ (df e = nk)
- df t : လွတ်လပ်မှု စုစုပေါင်းဒီဂရီ (df t = n-1)
- k: အဖွဲ့စုစုပေါင်းအရေအတွက်
- n: စုစုပေါင်းလေ့လာတွေ့ရှိချက်
- MSR- ပျမ်းမျှစတုရန်းဆုတ်ယုတ်မှု (MSR = SSR/df r )
- MSE- ပျမ်းမျှစတုရန်းအမှား (MSE = SSE/df e )
- F- F စမ်းသပ်မှုစာရင်းအင်း (F = MSR/MSE)
- p- F dfr၊ dfe နှင့် သက်ဆိုင်သော p တန်ဖိုး
p-value သည် ရွေးချယ်ထားသော အရေးပါမှုအဆင့် (ဥပမာ 0.05) ထက်နည်းပါက null hypothesis ကို ငြင်းပယ်နိုင်ပြီး အနည်းဆုံး လူဦးရေ၏ အဓိပ္ပါယ်သည် အခြားနည်းများနှင့် ကွဲပြားသည်ဟု ကောက်ချက်ချနိုင်သည်။
မှတ်ချက်- null hypothesis ကို သင် ငြင်းပယ်ပါက၊ အနည်းဆုံး လူဦးရေ၏ အဓိပ္ပါယ်သည် အခြားသူများနှင့် ကွဲပြားကြောင်း ညွှန်ပြနေသော်လည်း ANOVA ဇယားတွင် မည်သည့် လူဦးရေ အဓိပ္ပာယ် ကွာခြားသည်ကို မသတ်မှတ်ပါ။ ဒါကို ဆုံးဖြတ်ဖို့အတွက်၊ “ multiple comparison” testing လို့လည်း ခေါ်တဲ့ post hoc testing လုပ်ဖို့လိုအပ်ပါတယ်။
One-way ANOVA- ဥပမာ
မတူညီသော စာမေးပွဲပြင်ဆင်မှု ပရိုဂရမ်သုံးခုသည် ပေးထားသော စာမေးပွဲတစ်ခုတွင် မတူညီသော ပျမ်းမျှရမှတ်များ ဖြစ်ပေါ်လာခြင်း ရှိ၊မရှိ သိလိုသည်ဆိုပါစို့။ ဤအရာကို စမ်းသပ်ရန်အတွက် ကျွန်ုပ်တို့သည် လေ့လာမှုတစ်ခုတွင် ပါဝင်ရန် ကျောင်းသား 30 ကို စုဆောင်းပြီး ၎င်းတို့ကို အုပ်စုသုံးစုခွဲထားသည်။
အုပ်စုတစ်ခုစီရှိ ကျောင်းသားများသည် စာမေးပွဲအတွက် ပြင်ဆင်ရန် အောက်ပါသုံးပတ်အတွက် စာမေးပွဲပြင်ဆင်မှု ပရိုဂရမ်သုံးခုထဲမှ တစ်ခုကို အသုံးပြုရန် ကျပန်းသတ်မှတ်ပေးထားသည် ။ သုံးပတ်အဆုံးတွင် ကျောင်းသားအားလုံး စာမေးပွဲကို အတူတူဖြေဆိုကြသည်။
အုပ်စုတစ်ခုစီအတွက် စာမေးပွဲရလဒ်များကို အောက်တွင် ဖော်ပြထားသည်။
ဤဒေတာအတွက် တစ်လမ်းသွား ANOVA ကို လုပ်ဆောင်ရန်၊ ကျွန်ုပ်တို့သည် အောက်ဖော်ပြပါ ထည့်သွင်းမှုဖြင့် စာရင်းအင်းတစ်ကြောင်း ANOVA ဂဏန်းတွက်စက်ကို အသုံးပြုပါမည်။
အထွက်ဇယားမှ F test statistic သည် 2.358 ဖြစ်ပြီး သက်ဆိုင်သော p-value သည် 0.11385 ဖြစ်သည် ။
ဤ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။
ဆိုလိုသည်မှာ အုပ်စုသုံးစု၏ ပျမ်းမျှစာမေးပွဲရမှတ်များကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက် ရှိသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထား မရှိပါ။
ထပ်လောင်းအရင်းအမြစ်များ
အောက်ဖော်ပြပါ ဆောင်းပါးများသည် မတူညီသော စာရင်းအင်းဆော့ဖ်ဝဲကို အသုံးပြု၍ တစ်လမ်းသွား ANOVA ကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-
Excel တွင် One-Way ANOVA လုပ်ဆောင်နည်း
တစ်လမ်းမောင်း ANOVA ကို R ဖြင့် မည်သို့လုပ်ဆောင်ရမည်နည်း။
Python တွင် One-Way ANOVA လုပ်ဆောင်နည်း
SAS တွင် one-way ANOVA လုပ်ဆောင်နည်း
SPSS တွင် One-Way ANOVA လုပ်ဆောင်နည်း
Stata တွင် one-way ANOVA လုပ်ဆောင်နည်း
TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် One-Way ANOVA လုပ်ဆောင်နည်း
အွန်လိုင်းတစ်ကြောင်း ANOVA ဂဏန်းတွက်စက်
စာရေးသူအကြောင်း
Benjamin Anderson
မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။