Spss တွင် one-way anova လုပ်ဆောင်နည်း

တစ်လမ်းသွား ANOVA ကို သုံးသော သို့မဟုတ် ထို့ထက်ပိုသော လွတ်လပ်သော အုပ်စုများကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားမှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည်။

ကျွန်ုပ်တို့သည် တုံ့ပြန်မှုကိန်းရှင်တစ်ခုပေါ်ရှိ ကြိုတင်ခန့်မှန်းကိန်းရှင် တစ်ခု၏ အကျိုးသက်ရောက်မှုကို ပိုင်းခြားစိတ်ဖြာသောကြောင့် ဤစမ်းသပ်မှုအမျိုးအစားကို တစ်လမ်းသွား ANOVA ဟုခေါ်သည်။

အကယ်၍ ကျွန်ုပ်တို့သည် တုံ့ပြန်မှုကိန်းရှင်တစ်ခုအပေါ် ကြိုတင်ခန့်မှန်းကိန်းရှင် နှစ်ခု၏ အကျိုးသက်ရောက်မှုကို စိတ်ဝင်စားပါက၊ ကျွန်ုပ်တို့သည် နှစ်လမ်းသွား ANOVA ကို လုပ်ဆောင်နိုင်သည်။

ဤသင်ခန်းစာသည် SPSS တွင် တစ်လမ်းသွား ANOVA ကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

ဥပမာ- SPSS ရှိ တစ်လမ်းမောင်း ANOVA

သုတေသီတစ်ဦးသည် လေ့လာမှုတစ်ခုတွင် ပါဝင်ရန် ကျောင်းသား 30 ကို ခေါ်ယူသည်ဆိုပါစို့။ ကျောင်းသားများကို စာမေးပွဲအတွက် ပြင်ဆင်ရန် နောက်လတွင် လေ့လာမှုနည်းစနစ်သုံးမျိုးထဲမှ တစ်ခုကို အသုံးပြုရန် ကျပန်းသတ်မှတ်ပေးထားသည်။ လကုန်တွင် ကျောင်းသားအားလုံး တူညီသော စာမေးပွဲကို ဖြေဆိုကြသည်။

ကျောင်းသားစာမေးပွဲရလဒ်များကို အောက်တွင်ဖော်ပြထားသည်-

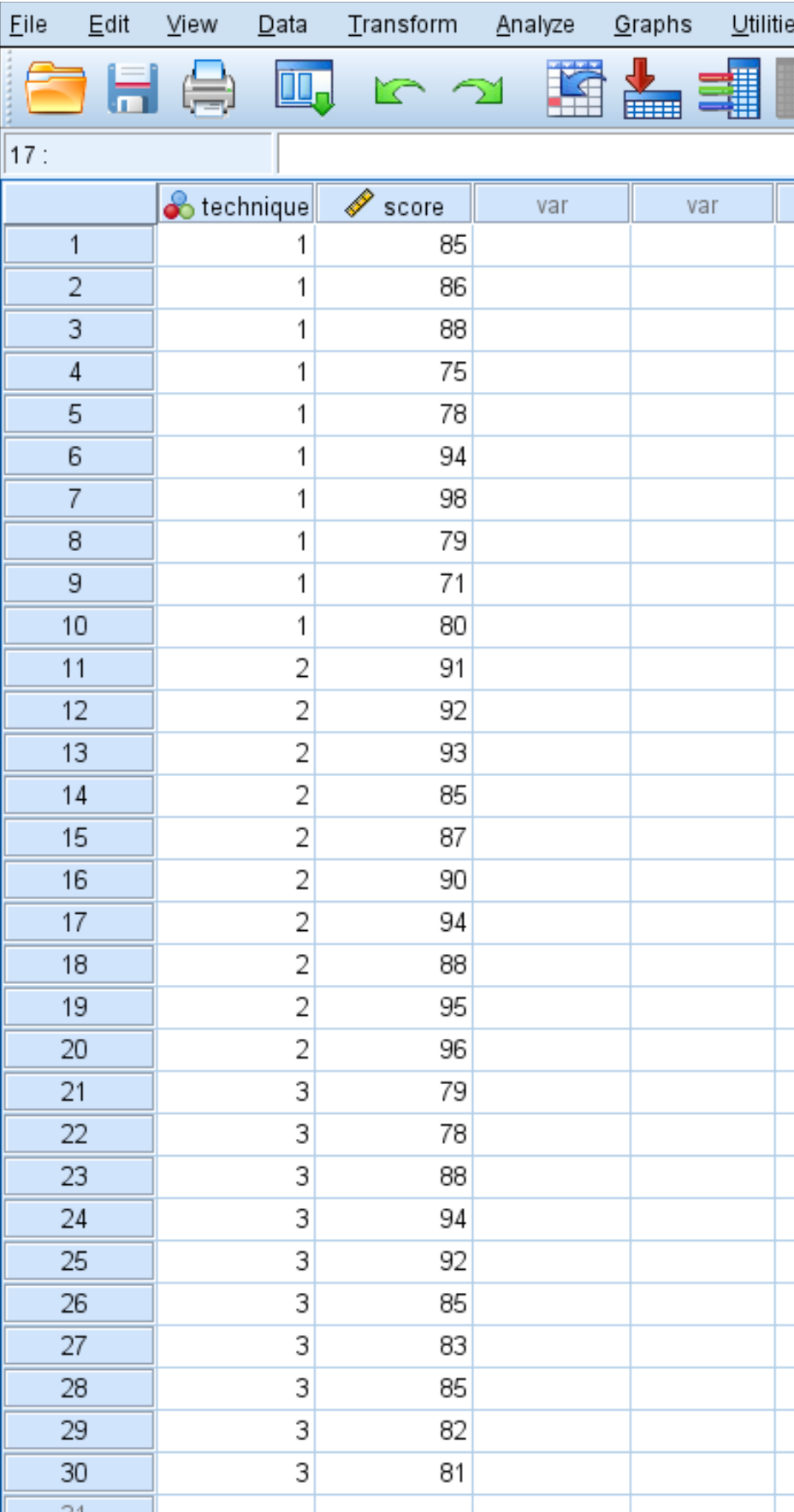
အုပ်စုသုံးစုတွင် ပျမ်းမျှရမှတ်များ တူညီခြင်းရှိမရှိ ဆုံးဖြတ်ရန် တစ်ကြောင်း ANOVA လုပ်ဆောင်ရန် အောက်ပါအဆင့်များကို အသုံးပြုပါ။

အဆင့် 1- ဒေတာကို မြင်ယောင်ကြည့်ပါ။

ပထမဦးစွာ၊ လေ့လာမှုနည်းလမ်းသုံးခုတစ်ခုစီအတွက် စာမေးပွဲရမှတ်များခွဲဝေမှုကို မြင်သာစေရန် ကွက်လပ်များကို ဖန်တီးပါမည်။ Charts tab ကိုနှိပ်ပါ၊ ထို့နောက် Chart Builder ကို နှိပ်ပါ။

Choose from: window တွင် Boxplot ကို ရွေးပါ။ ထို့နောက် Simple boxplot ဟုအမည်တပ်ထားသော ပထမဇယားကို ပင်မတည်းဖြတ်သည့်ဝင်းဒိုးသို့ ဆွဲယူပါ။ x-axis ပေါ်ရှိ နည်းပညာဆိုင်ရာ ကိန်းရှင်နှင့် y-ဝင်ရိုးပေါ်ရှိ ရမှတ်များကို ဆွဲယူပါ။

ထို့နောက် Element Properties ကို နှိပ်ပါ၊ ထို့နောက် Y1 Axis ကိုနှိပ်ပါ ။ အနိမ့်ဆုံး တန်ဖိုးကို 60 သို့ပြောင်းပါ။ ထို့နောက် OK ကိုနှိပ်ပါ။

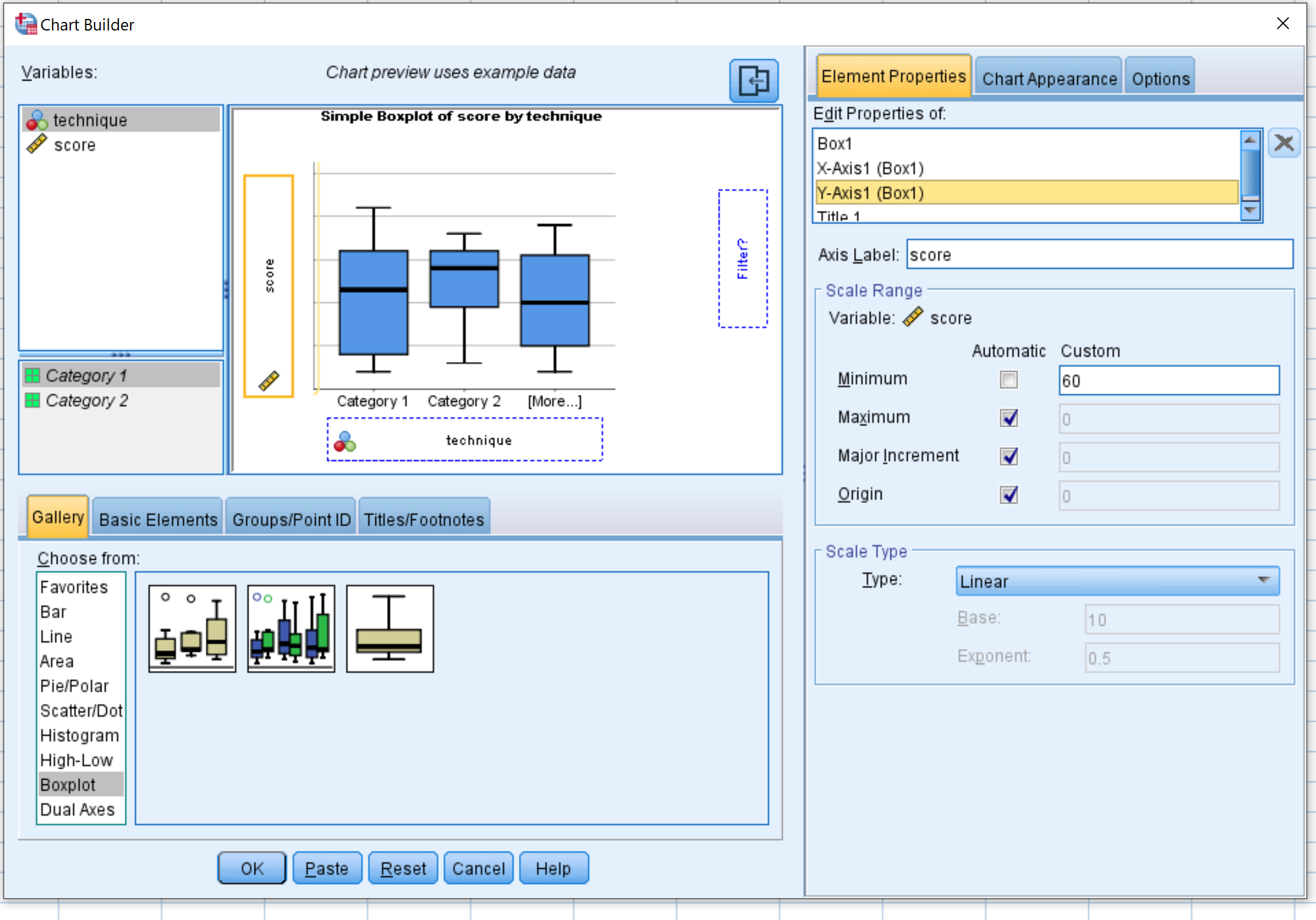
အောက်ပါအကွက်များ ပေါ်လာပါမည်-

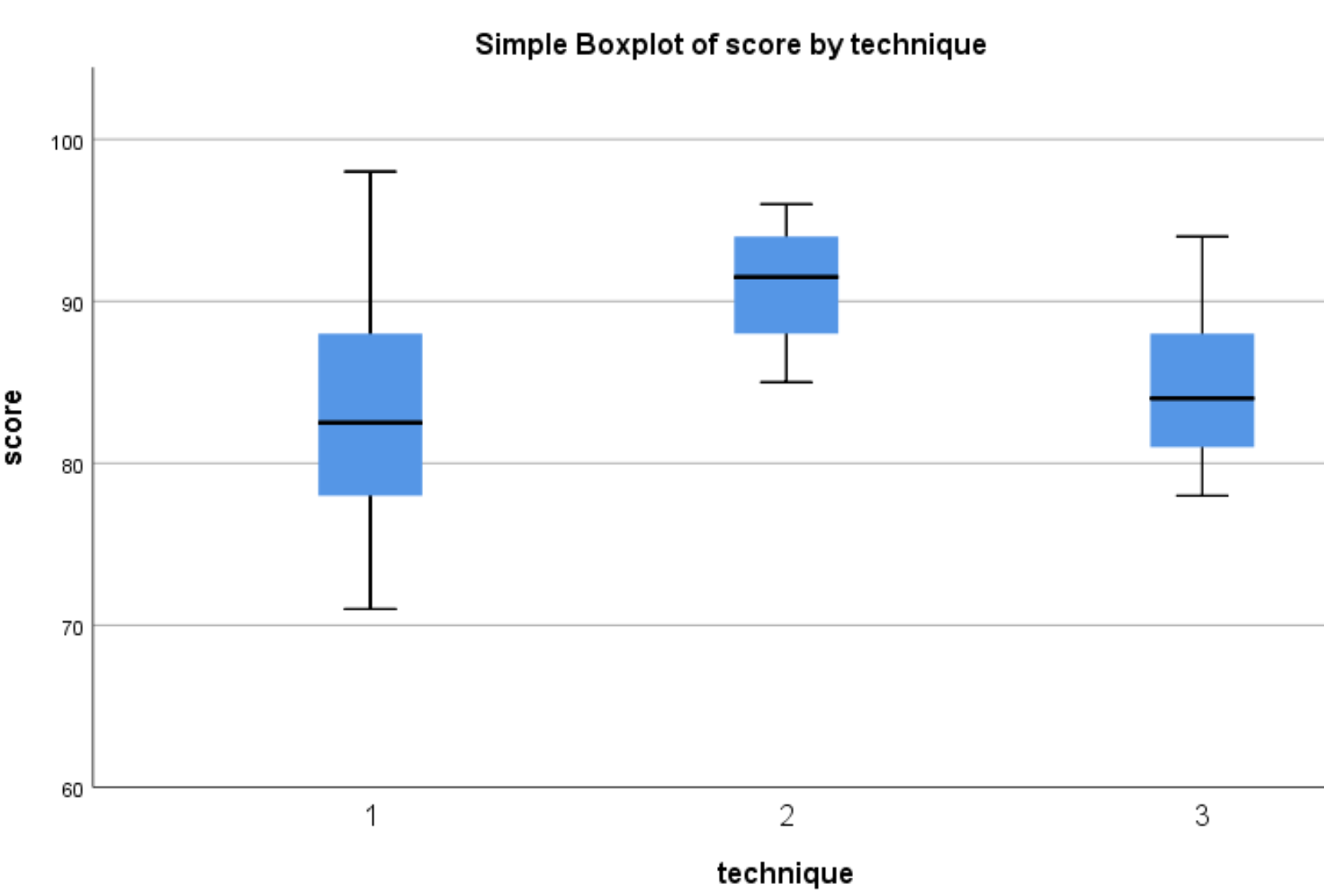
Technique 1 နှင့် 3 ကိုအသုံးပြုသောကျောင်းသားများထက် Technique 2 ကိုအသုံးပြုသောကျောင်းသားများအတွက် စာမေးပွဲရမှတ်များခွဲဝေမှုသည်ပိုမိုမြင့်မားကြောင်းကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။ ဤရမှတ်ကွာခြားချက်များသည် ကိန်းဂဏန်းအရသိသာထင်ရှားမှုရှိမရှိဆုံးဖြတ်ရန်၊ တစ်လမ်းတည်း ANOVA ကိုလုပ်ဆောင်ပါမည်။

အဆင့် 2- တစ်လမ်းမောင်း ANOVA လုပ်ဆောင်ပါ။

ခွဲခြမ်းစိတ်ဖြာခြင်း tab ကို နှိပ်ပါ၊ ထို့နောက် Means ကို နှိုင်းယှဉ်ပါ ၊ ထို့နောက် One-Way ANOVA ကိုနှိပ်ပါ ။

ပေါ်လာသည့် ဝင်းဒိုးအသစ်တွင်၊ မှီခိုစာရင်းဟု တံဆိပ်တပ်ထားသော အကွက်တွင် ပြောင်းနိုင်သော ရမှတ်ကို Factor တံဆိပ်တပ်ထားသော အကွက်တွင် ပြောင်းလဲနိုင်သော နည်းပညာကို ထားလိုက်ပါ။

ထို့နောက် Post Hoc ကိုနှိပ်ပြီး Tukey ဘေးရှိ အကွက်ကို အမှန်ခြစ်ပေးပါ။ ထို့နောက် Continue ကိုနှိပ်ပါ။

ထို့နောက် Options ကို နှိပ်ပြီး Descriptive ဘေးရှိ အကွက်ကို အမှန်ခြစ်ပါ။ ထို့နောက် Continue ကိုနှိပ်ပါ။

နောက်ဆုံးအနေနဲ့ OK ကို နှိပ်ပါ။

အဆင့် 3- ရလဒ်ကို ဘာသာပြန်ပါ။

OK ကိုနှိပ်ပြီးသည်နှင့်တစ်ကြောင်း ANOVA ရလဒ်များပေါ်လာလိမ့်မည်။ ဤသည်မှာ ရလဒ်ကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-

ဇယားဖော်ပြချက်

ဤဇယားသည် ကျွန်ုပ်တို့၏ဒေတာအတွဲရှိ အုပ်စုသုံးစုမှ တစ်ခုစီအတွက် သရုပ်ဖော်ကိန်းဂဏန်းများကို ပြသသည်။

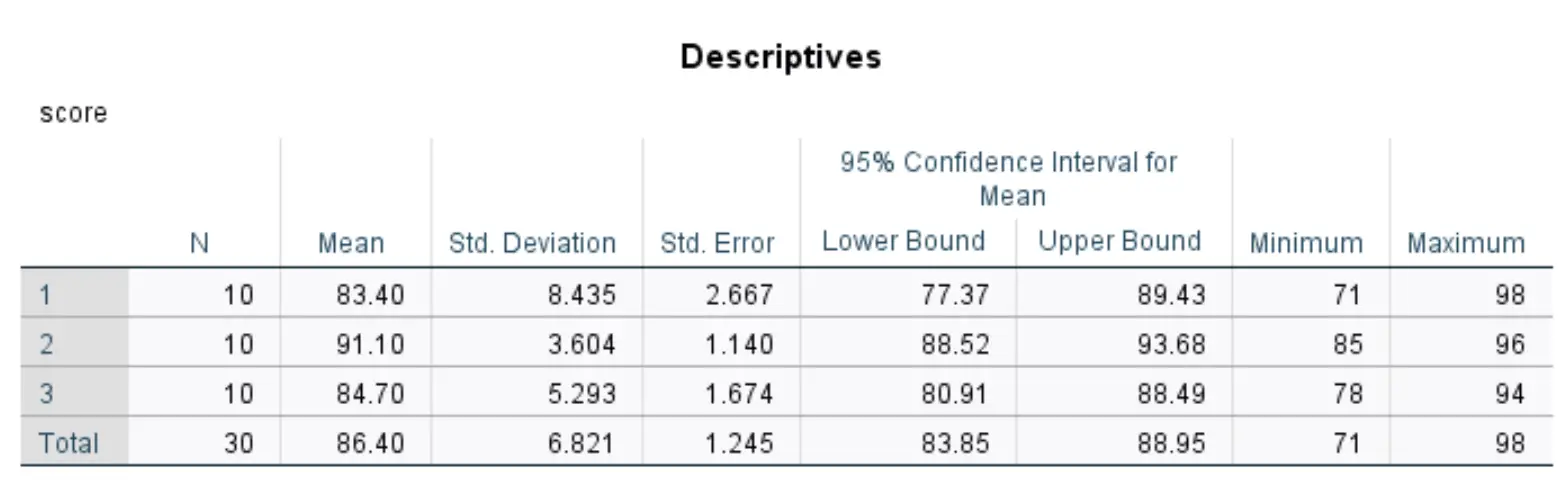
အသက်ဆိုင်ဆုံး ကိန်းဂဏန်းများမှာ-

• N- အဖွဲ့တစ်ခုစီရှိ ကျောင်းသားဦးရေ။
• ပျမ်းမျှ- အုပ်စုတစ်ခုစီအတွက် ပျမ်းမျှစာမေးပွဲရမှတ်။
• စံ။ သွေဖည်မှု- အုပ်စုတစ်ခုစီအတွက် စမ်းသပ်မှုရလဒ်များ၏ စံသွေဖည်မှု။

ANOVA စားပွဲ

ဤဇယားသည် တစ်လမ်းသွား ANOVA ၏ရလဒ်များကို ပြသသည်-

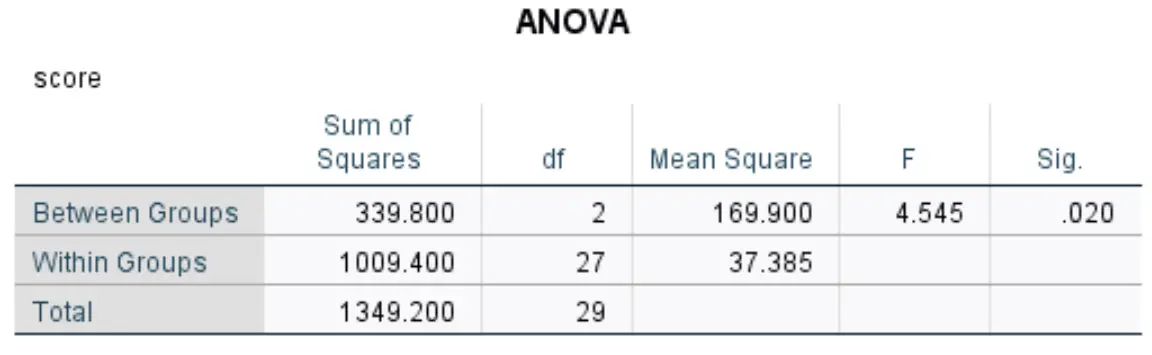
အသက်ဆိုင်ဆုံး ကိန်းဂဏန်းများမှာ-

• F: အလုံးစုံ F စာရင်းအင်း။
• Sig- ပိုင်း ဝေ df (2) နှင့် ပိုင်းခြေ df (27) တို့နှင့်အတူ F ကိန်းဂဏန်း (4.545) နှင့် သက်ဆိုင်သည့် p-တန်ဖိုး။ ဤကိစ္စတွင်၊ p-value သည် 0.020 ဖြစ်သွားသည်။

တစ်လမ်းသွား ANOVA သည် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြုကြောင်း သတိရပါ။

• H ₀ ( null hypothesis ) : μ ₁ = μ ₂ = μ ₃ = … = μ _k (လူဦးရေအားလုံးသည် တူညီသည်)
• H _A (အခြားသောယူဆချက်)- အနည်းဆုံး လူဦးရေ ဆိုသည်မှာ ကွဲပြားသည်။   အနားယူပါ။

ANOVA ဇယား၏ p-value သည် 0.05 ထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့တွင် null hypothesis ကို ငြင်းဆိုရန် လုံလောက်သော အထောက်အထားများရှိပြီး အနည်းဆုံး အုပ်စု၏ ဆိုလိုသည်မှာ အခြားနည်းများနှင့် ကွဲပြားသည်ဟု ကောက်ချက်ချနိုင်သည်။

ဘယ်အုပ်စုက တစ်ခုနဲ့တစ်ခု ကွာခြားတယ်ဆိုတာ အတိအကျသိဖို့အတွက် ANOVA ရလဒ်ရဲ့ နောက်ဆုံးဇယားကို ကိုးကားနိုင်ပါတယ်။

နှိုင်းယှဉ်မှုဇယား

ဤဇယားသည် အုပ်စုသုံးစုမှ တစ်ခုစီကြား Tukey ၏ post-hoc များစွာသော နှိုင်းယှဉ်မှုများကို ပြသသည်။ Sig ကို အဓိက စိတ်ဝင်စားတယ်။ ကော်လံ၊ အုပ်စုတစ်ခုစီကြားရှိ ခြားနားချက်များအတွက် p-တန်ဖိုးများကို ဖော်ပြသည်-

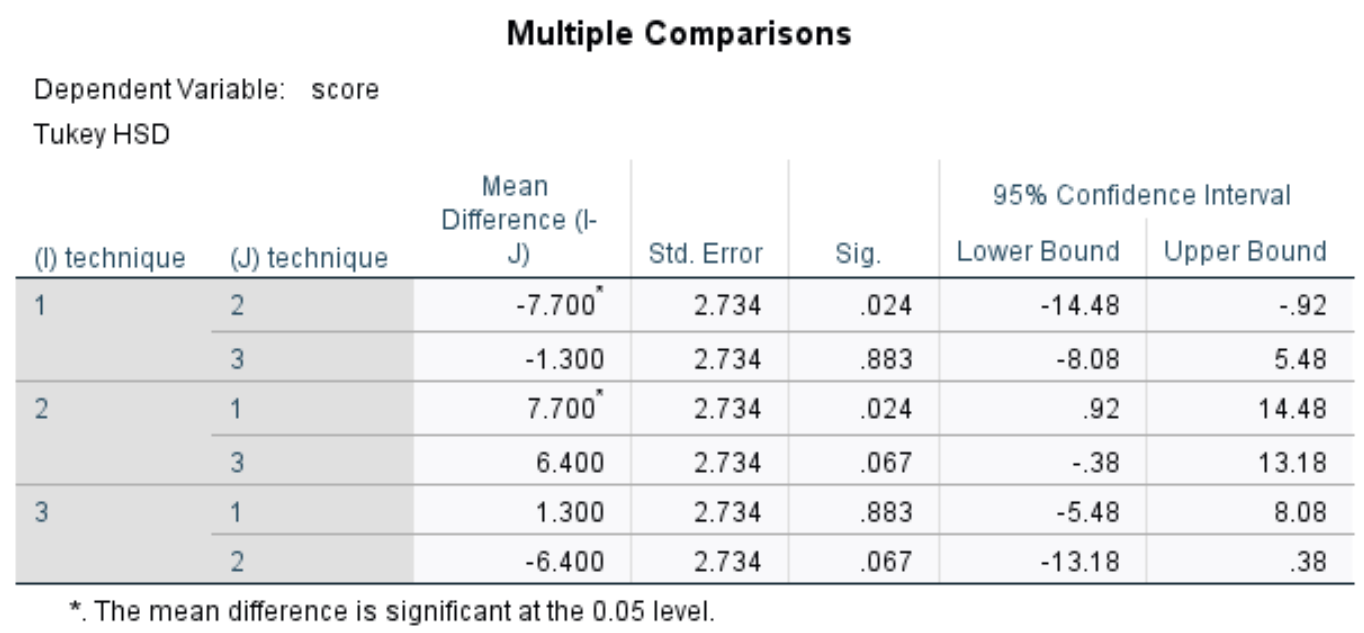
ဇယားတွင် အောက်ပါနှိုင်းယှဉ်မှုများအတွက် p-တန်ဖိုးများကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

• Technique 1 ဆန့်ကျင်ဘက် 2: | p-value = 0.024
• နည်းပညာ 1 ဆန့်ကျင်ဘက် 3 | p-value = 0.883
• Technique 2 ဆန့်ကျင်ဘက် 3 | p-value = 0.067

0.05 ထက်နည်းသော p-value နှင့် တစ်ခုတည်းသောအုပ်စုနှိုင်းယှဉ်မှုသည် Technique 1 နှင့် Technique 2 အကြားဖြစ်သည်။

Technique 1 ကိုအသုံးပြုသောကျောင်းသားများနှင့် Technique 2 ကိုအသုံးပြုသောကျောင်းသားများကြားတွင် ပျမ်းမျှစာမေးပွဲရမှတ်များတွင် ကိန်းဂဏန်းအချက်အလတ်သိသိသာသာကွာခြားမှုရှိကြောင်း ၎င်းကကျွန်ုပ်တို့အားပြောပြသည်။

သို့သော် နည်းစနစ် 1 နှင့် 3 အကြား၊ နည်းစနစ် 2 နှင့် 3 အကြားတွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ကွာခြားချက်မရှိပါ။

အဆင့် 4- ရလဒ်များကို သတင်းပို့ပါ။

နောက်ဆုံးတွင်၊ တစ်လမ်းမောင်း ANOVA ၏ရလဒ်များကို ကျွန်ုပ်တို့အစီရင်ခံနိုင်ပါသည်။ ဤသည်မှာ ဤအရာကို ပြုလုပ်ပုံ၏ ဥပမာတစ်ခုဖြစ်သည်။

မတူညီသော လေ့လာမှုနည်းပညာသုံးမျိုးသည် မတူညီသောစမ်းသပ်မှုရလဒ်များကိုဖြစ်ပေါ်စေခြင်းရှိမရှိ ဆုံးဖြတ်ရန် တစ်လမ်းသွား ANOVA ကို လုပ်ဆောင်ခဲ့သည်။

စုစုပေါင်းကျောင်းသား ၁၀ ဦးသည် တူညီသောစမ်းသပ်မှုမပြုလုပ်မီ တစ်လကြာ လေ့လာမှုသုံးခုမှ တစ်ခုစီကို အသုံးပြုခဲ့သည်။

တစ်ကြောင်း ANOVA သည် အနည်းဆုံးအုပ်စုနှစ်စုကြားရှိ စာမေးပွဲရမှတ်များတွင် ကိန်းဂဏန်းသိသာထင်ရှားသော ကွာခြားချက်ရှိသည် (F(2၊ 27) = 4.545၊ p = 0.020)။

နှိုင်းယှဉ်မှုများစွာအတွက် Tukey ၏စမ်းသပ်မှုတွင် ပျမ်းမျှစာမေးပွဲရမှတ်များသည် Technique 1 နှင့် Technique 2 (p = 0.024၊ 95% CI = [-14.48၊ -0.92]) ကိုအသုံးပြုသောကျောင်းသားများကြားတွင် သိသိသာသာကွာခြားကြောင်း ထုတ်ဖော်ပြသခဲ့သည်။

နည်းစနစ် 1 နှင့် 3 အတွက် ရမှတ်များ (p = 0.883) သို့မဟုတ် နည်းစနစ် 2 နှင့် 3 (p = 0.067) ကြားတွင် ကိန်းဂဏန်း သိသိသာသာ ကွာခြားမှု မရှိခဲ့ပါ။