Excel တွင် p တန်ဖိုးများကို တွက်ချက်နည်း (ဥပမာ 3 ခု)

စာရင်းဇယားများတွင်၊ လူဦးရေကန့်သတ်ချက် တစ်ခု၏ထုတ်ပြန်ချက်သည် မှန်ကန်သည်ဖြစ်စေ မမှန်ကန်ကြောင်း ဆုံးဖြတ်ရန် သီအိုရီစစ်ဆေးမှုကို ကျွန်ုပ်တို့အသုံးပြုသည်။

ကျွန်ုပ်တို့သည် သီအိုရီစမ်းသပ်မှုတစ်ခုကို လုပ်ဆောင်သောအခါ၊ ကျွန်ုပ်တို့သည် T-score စမ်းသပ်မှုစာရင်းအင်းကို ပေးလေ့ရှိသည်။

ဤ t-score စစ်ဆေးမှု ကိန်းဂဏန်းကို ရှာတွေ့သည်နှင့် ၎င်းနှင့် ဆက်စပ်နေသည့် p-value ကို ရှာတွေ့နိုင်ပါသည်။

ဤ p-value သည် သတ်မှတ်ထားသောတန်ဖိုးထက်နည်းနေပါက (ဥပမာ 0.10၊ 0.05၊ 0.01)၊ ထို့နောက် စမ်းသပ်မှု၏ null hypothesis ကို ငြင်းပယ်ပြီး ကျွန်ုပ်တို့၏ရလဒ်များသည် စာရင်းအင်းအရ သိသာထင်ရှားသည်ဟု ကောက်ချက်ချပါသည်။

အောက်ဖော်ပြပါနမူနာများသည် Excel တွင် စမ်းသပ်စာရင်းအင်းတစ်ခုအတွက် p-value ကို ကွဲပြားသောအခြေအနေသုံးမျိုးဖြင့် တွက်ချက်နည်းကို ပြသထားသည်။

ဥပမာ 1- အမြီးနှစ်ကြောင်းစမ်းသပ်မှုအတွက် P တန်ဖိုးကို တွက်ချက်ပါ။

ရုက္ခဗေဒပညာရှင်တစ်ဦးသည် အပင်မျိုးစိတ်များ၏ ပျမ်းမျှအမြင့်သည် 15 လက်မနှင့် ညီမျှသည်ဆိုပါစို့။

အပင် ၁၂ ပင်၏ ကျပန်းနမူနာတစ်ခုတွင် ၊ နမူနာ၏ ပျမ်းမျှအမြင့်မှာ ၁၄.၃၃ လက်မဖြစ်ပြီး နမူနာ၏စံသွေဖည်မှုမှာ ၁.၃၇ လက်မဖြစ်ကြောင်း သူမတွေ့ရှိခဲ့သည်။

၎င်းသည် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြု၍ သီအိုရီစစ်ဆေးမှုကို လုပ်ဆောင်သည်-

H ₀ (null hypothesis): μ= 15 လက်မ

H _A (အစားထိုးယူဆချက်): μ ≠ 15 လက်မ

စာမေးပွဲစာရင်းကို အောက်ပါအတိုင်း တွက်ချက်သည်။

• t = ( X – µ) / (s/ √n )
• t = (14.33-15) / (1.37/√ 12 )
• t = -1.694

ဤစမ်းသပ်မှုစာရင်းအင်းနှင့်ဆက်စပ်သော လွတ်လပ်မှုဒီဂရီများမှာ n-1 = 12-1 = 11 ဖြစ်သည်။

ဤစမ်းသပ်မှုစာရင်းအင်းအတွက် p-value ကိုရှာရန်၊ Excel တွင် အောက်ပါဖော်မြူလာကို အသုံးပြုပါမည်။

 =T.DIST.2T(ABS(-1.694), 11)

အောက်ဖော်ပြပါ ဖန်သားပြင်ဓာတ်ပုံသည် ဤဖော်မြူလာကို လက်တွေ့တွင် အသုံးပြုနည်းကို ပြသထားသည်။

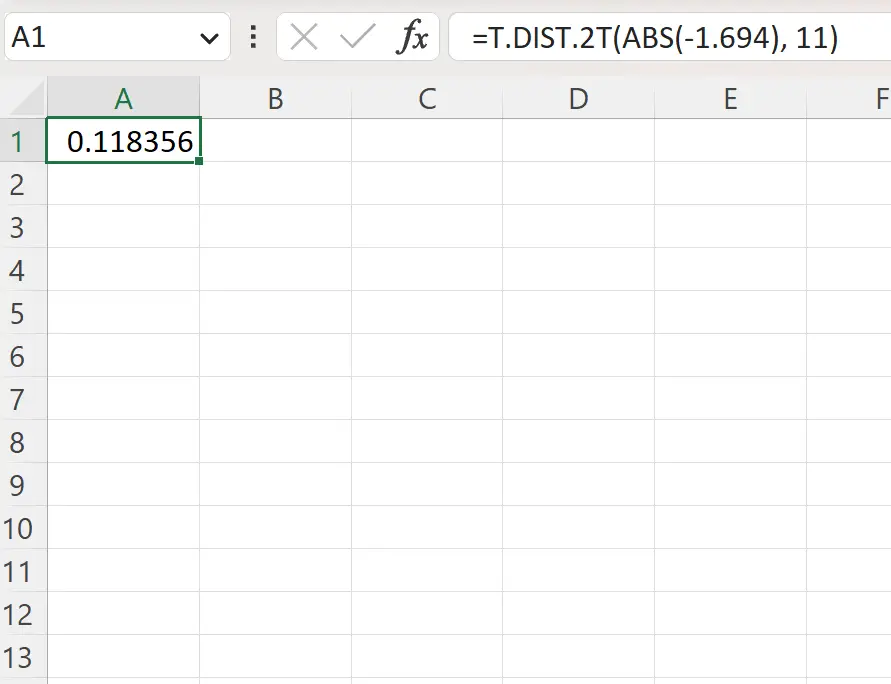
အမြီးနှစ်ချောင်း p-value သည် 0.1184 ဖြစ်သည်။

ဒီကတည်းက တန်ဖိုးရှိတယ်။ 0.05 ထက်မနည်းပါ၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။ ပျမ်းမျှအပင်၏ အမြင့်သည် ၁၅ လက်မထက် ကွာခြားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထား မရှိပါ။

ဥပမာ 2- ဘယ်ဘက်ရှိ စမ်းသပ်မှုအတွက် P တန်ဖိုးကို တွက်ချက်ပါ။

စက်ရုံတစ်ခုတွင်ထုတ်လုပ်သည့် gadget တစ်ခု၏ပျမ်းမျှအလေးချိန်မှာ 20 ဂရမ်ဖြစ်သည်ဆိုပါစို့။ သို့ရာတွင်၊ စစ်ဆေးရေးမှူးတစ်ဦးသည် အမှန်တကယ် ပျမ်းမျှအလေးချိန် 20 ဂရမ်အောက်ရှိမည်ဟု ခန့်မှန်းသည်။

၎င်းကို စမ်းသပ်ရန်၊ ၎င်းသည် ဝစ်ဂျက် 20 ၏ ရိုးရှင်းသော ကျပန်းနမူနာကို အလေးချိန်ပေးပြီး အောက်ပါအချက်အလက်များကို ရရှိသည်-

• n = ဝစ်ဂျက် 20
• x = 19.8 ဂရမ်
• s = 3.1 ဂရမ်

ထို့နောက် ၎င်းသည် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြု၍ သီအိုရီစစ်ဆေးမှုကို လုပ်ဆောင်သည်-

H ₀ (null hypothesis): μ ≥ 20 ဂရမ်

H _A (အခြားယူဆချက်): μ < 20 ဂရမ်

စာမေးပွဲစာရင်းကို အောက်ပါအတိုင်း တွက်ချက်သည်။

• t = ( X – µ) / (s/ √n )
• t = (19.8-20) / (3.1/√ 20 )
• t = -.2885

ဤစမ်းသပ်မှုစာရင်းအင်းနှင့်ဆက်စပ်သော လွတ်လပ်မှုဒီဂရီများမှာ n-1 = 20-1 = 19 ဖြစ်သည်။

ဤစမ်းသပ်မှုစာရင်းအင်းအတွက် p-value ကိုရှာရန်၊ Excel တွင် အောက်ပါဖော်မြူလာကို အသုံးပြုပါမည်။

 =T.DIST(-.2885, 19, TRUE)

အောက်ဖော်ပြပါ ဖန်သားပြင်ဓာတ်ပုံသည် ဤဖော်မြူလာကို လက်တွေ့တွင် အသုံးပြုနည်းကို ပြသထားသည်။

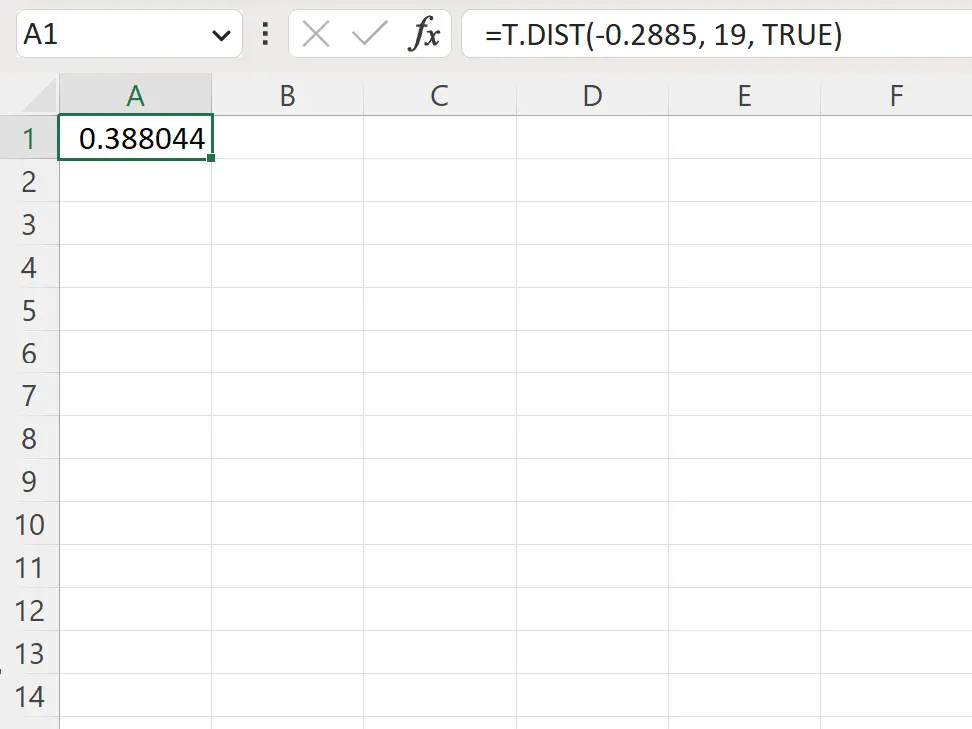
ဘယ်ဘက်ရှိ p-တန်ဖိုးသည် 0.388044 ဖြစ်သည်။

ဒီကတည်းက တန်ဖိုးရှိတယ်။ 0.05 ထက်မနည်းပါ၊ စစ်ဆေးသူသည် null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။ ဤစက်ရုံတွင် ထုတ်လုပ်သည့် ဝစ်ဂျက်များ၏ ပျှမ်းမျှ အလေးချိန်မှာ 20 ဂရမ်ထက် နည်းသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထား မရှိပါ။

မှတ်ချက် – p-value ကို တွက်ချက်ရာတွင် စုစည်းဖြန့်ဝေမှု လုပ်ဆောင်ချက်ကို အသုံးပြုသင့်သည်ဟု သတ်မှတ်ရန် ကျွန်ုပ်တို့သည် TRUE အငြင်းအခုံကို အသုံးပြုခဲ့သည်။

ဥပမာ 3- ညာဘက်အမြီးပိုင်းစမ်းသပ်မှုအတွက် P တန်ဖိုးကို တွက်ချက်ပါ။

အပင်မျိုးစိတ်တစ်ခု၏ ပျမ်းမျှအမြင့်သည် 10 လက်မဟု ယူဆကြပါစို့။ သို့သော် ရုက္ခဗေဒပညာရှင်တစ်ဦး၏ အဆိုအရ ပျမ်းမျှအရပ်သည် ၁၀လက်မကျော်သာရှိသည်။

ဤတိုင်ကြားချက်ကို စမ်းသပ်ရန်၊ သူမသည် ရိုးရိုးကျပန်းနမူနာ ၁၅ ပင်၏ အမြင့်ကို တိုင်းတာပြီး အောက်ပါအချက်အလက်များကို ရယူသည်-

• n=အပင် ၁၅
• x = ၁၁.၄ လက်မ
• s = 2.5 လက်မ

ထို့နောက် ၎င်းသည် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြု၍ သီအိုရီစစ်ဆေးမှုကို လုပ်ဆောင်သည်-

H ₀ (null hypothesis): μ ≤ 10 လက်မ

H _A (အစားထိုးယူဆချက်): μ > 10 လက်မ

စာမေးပွဲစာရင်းကို အောက်ပါအတိုင်း တွက်ချက်သည်။

• t = ( X – µ) / (s/ √n )
• t = (11.4-10) / (2.5/√ 15 )
• t = 2.1689

ဤစမ်းသပ်မှုစာရင်းအင်းနှင့်ဆက်စပ်သော လွတ်လပ်မှုဒီဂရီများမှာ n-1 = 15-1 = 14 ဖြစ်သည်။

ဤစမ်းသပ်မှုစာရင်းအင်းအတွက် p-value ကိုရှာရန်၊ Excel တွင် အောက်ပါဖော်မြူလာကို အသုံးပြုပါမည်။

 =T.DIST.RT(2.1689, 14)

အောက်ဖော်ပြပါ ဖန်သားပြင်ဓာတ်ပုံသည် ဤဖော်မြူလာကို လက်တွေ့တွင် အသုံးပြုနည်းကို ပြသထားသည်။

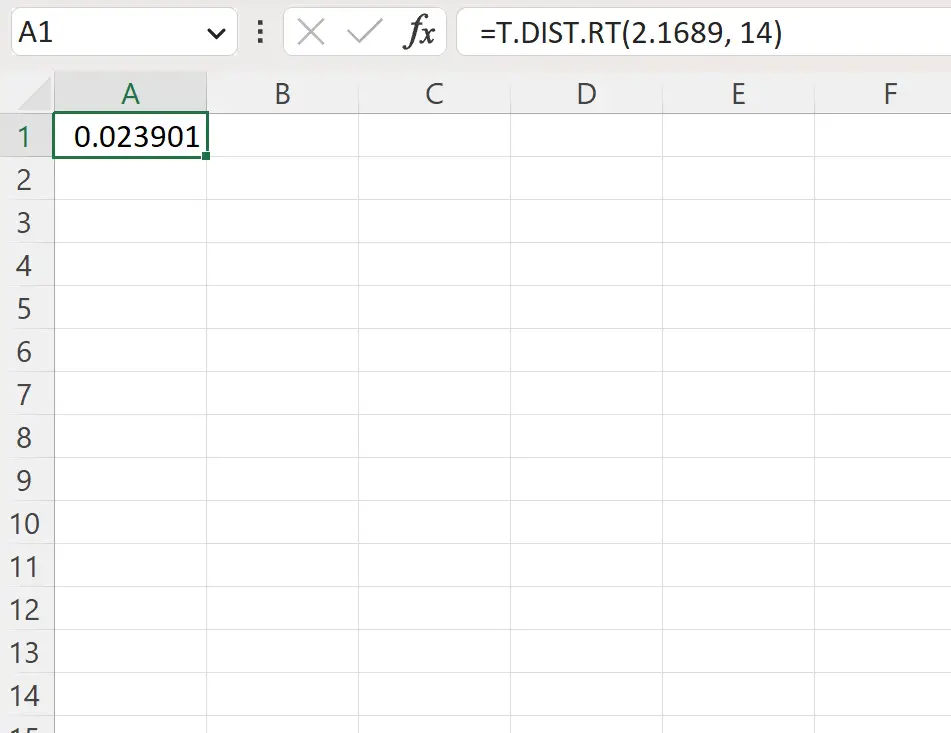
ညာဘက်ရှိ p-တန်ဖိုးသည် 0.023901 ဖြစ်သည်။

ဤတန်ဖိုးသည် 0.05 ထက်နည်းသောကြောင့် ရုက္ခဗေဒပညာရှင်သည် null hypothesis ကို ငြင်းပယ်နိုင်သည်။ ဤအပင်မျိုးစိတ်များ၏ ပျမ်းမျှအမြင့်မှာ ၁၀ လက်မကျော်ရှိသည်ဟု ပြောရန် လုံလောက်သော အထောက်အထားရှိသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် Excel တွင် အခြားသော အသုံးများသော အလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

Excel တွင် Z ရမှတ်မှ P Value ကိုဘယ်လိုရှာမလဲ။
Excel တွင် F ကိန်းဂဏန်းတစ်ခု၏ P တန်ဖိုးကို မည်သို့ရှာမည်နည်း။
Excel တွင် Chi-square ကိန်းဂဏန်းတစ်ခု၏ P တန်ဖိုးကို မည်သို့ရှာမည်နည်း။