Pareto ဖြန့်ဖြူးခြင်း။

အားဖြင့် ဩဂုတ် 3, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် Pareto ဖြန့်ဝေမှုသည် စာရင်းအင်းများတွင် အဘယ်အရာနှင့် ၎င်းကိုအသုံးပြုကြောင်းကို ရှင်းပြထားသည်။ Pareto ဖြန့်ဖြူးရေးဂရပ်နှင့် ဤဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုအမျိုးအစား၏ ဂုဏ်သတ္တိများကိုလည်း သင်တွေ့မြင်နိုင်မည်ဖြစ်ပါသည်။

Pareto ဖြန့်ဖြူးခြင်းဆိုသည်မှာ အဘယ်နည်း။

Pareto ဖြန့်ဝေမှုသည် Pareto နိယာမကို နမူနာယူရန် ကိန်းဂဏန်းစာရင်းဇယားများတွင် အသုံးပြုသည့် စဉ်ဆက်မပြတ်ဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။ ထို့ကြောင့် Pareto ဖြန့်ဖြူးမှုသည် ကျန်တန်ဖိုးများထက် များစွာပို၍ ဖြစ်နိုင်ခြေရှိသော တန်ဖိုးအနည်းငယ်ရှိသော ဖြစ်နိုင်ခြေဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။

80-20 စည်းမျဉ်းဟုလည်း ခေါ်သော Pareto ၏ဥပဒေသည် ဖြစ်စဉ်တစ်ခု၏အကြောင်းရင်းအများစုသည် လူဦးရေ၏အနည်းစုကြောင့်ဖြစ်သည်ဟု ကိန်းဂဏန်းဆိုင်ရာနိယာမတစ်ခုဖြစ်ကြောင်း သတိရပါ။

Pareto ဖြန့်ဖြူးမှုတွင် ထူးခြားသော ကန့်သတ်ဘောင်နှစ်ခု ရှိသည်- စကေး ကန့်သတ်ဘောင် x m နှင့် ပုံသဏ္ဍာန် ကန့်သတ်ချက် α။

X\sim \text{Pareto}(\alpha,x_m)

မူလက Pareto ဖြန့်ဖြူးမှုကို လူဦးရေအတွင်း ကြွယ်ဝချမ်းသာမှု ခွဲဝေမှုကို ဖော်ပြရန်အတွက် အသုံးပြုခဲ့ခြင်းဖြစ်ပြီး အများစုမှာ လူဦးရေအချိုးအစား အနည်းငယ်ကြောင့်ဖြစ်သည်။ သို့သော် လက်ရှိတွင် Pareto ဖြန့်ဖြူးမှုတွင် အရည်အသွေးထိန်းချုပ်မှု၊ စီးပွားရေး၊ သိပ္ပံ၊ လူမှုရေးနယ်ပယ်စသည်ဖြင့် အသုံးချမှုများစွာရှိသည်။

Pareto ဖြန့်ဖြူးမှုကို ဖြန့်ဖြူးမှုကို ရေးဆွဲခဲ့သူ စီးပွားရေးပညာရှင် Vilfredo Pareto ကို အစွဲပြု၍ အမည်ပေးထားသည်။ သို့သော်၊ သူသည် Pareto ဇယားအတွက်အကောင်းဆုံးလူသိများသည်။

Pareto ဖြန့်ဖြူးရေးဇယား

ယခု ကျွန်ုပ်တို့သည် Pareto ဖြန့်ဖြူးခြင်း၏ အဓိပ္ပါယ်ကို သိရှိပြီး၊ ဂရပ်ဖစ်ဖြင့် ကိုယ်စားပြုထားသော Pareto ဖြန့်ဝေမှုများ၏ နမူနာများစွာကို ကြည့်ကြပါစို့။

ထို့ကြောင့်၊ Pareto ဖြန့်ဖြူးမှု၏သိပ်သည်းဆလုပ်ဆောင်မှု၏ဂရပ်သည် ၎င်း၏လက္ခဏာတန်ဖိုးများပေါ်မူတည်၍ အောက်တွင်ဖော်ပြထားသည်ကို သင်မြင်နိုင်သည်-

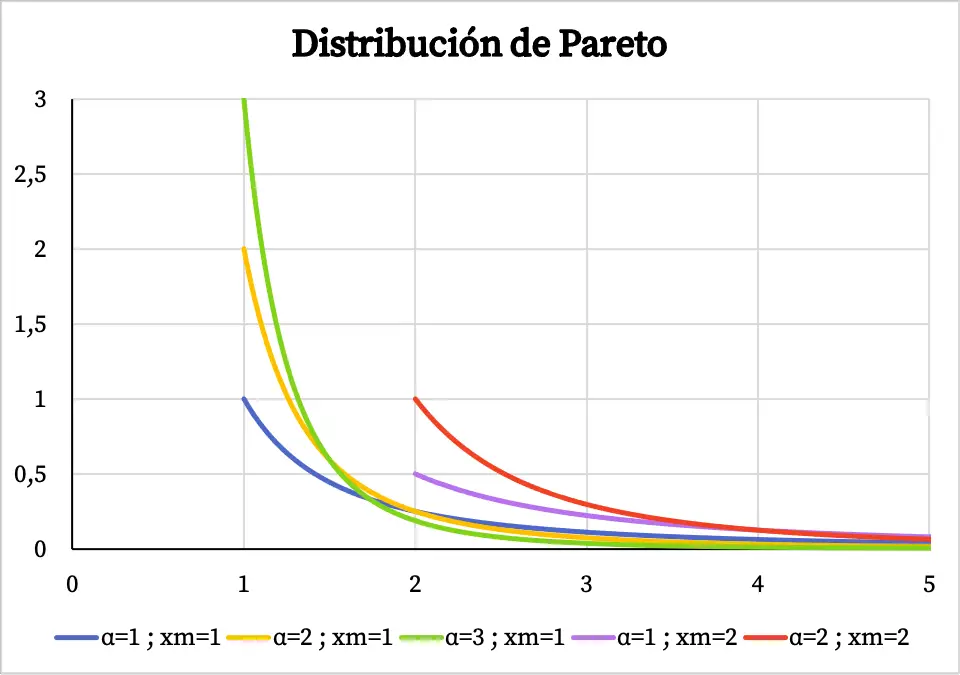
Pareto ဖြန့်ဝေမှုဇယား

Pareto ဖြန့်ဖြူးမှု၏ ဒိုမိန်းသည် x m တန်ဖိုးမှ +∞ သို့သွားသည်၊ ထို့ကြောင့် density function သည် x m တန်ဖိုး မတိုင်မီတွင် ရှိနေသည်ကို သတိပြုပါ။

အခြားတစ်ဖက်တွင်၊ Pareto ဖြန့်ဖြူးမှု၏ တိုးပွားလာနိုင်သည့် ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်၏ ဂရပ်သည် အောက်ပါအတိုင်းဖြစ်သည်-

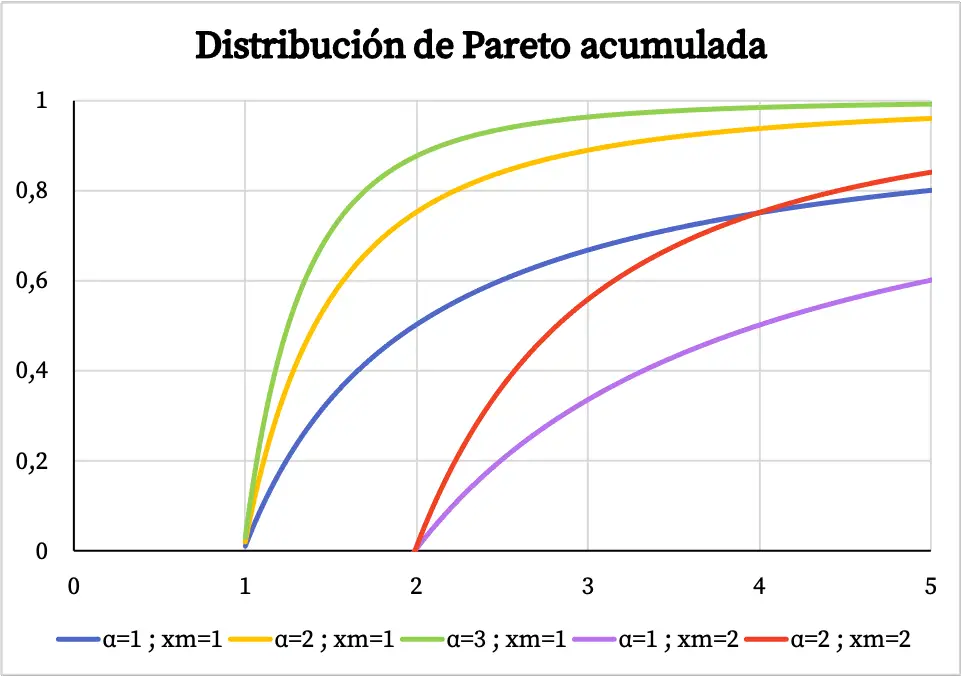
Pareto ဖြန့်ဖြူးမှု၏ စုစည်းဖြစ်နိုင်ခြေ

Pareto ဖြန့်ဖြူးခြင်း၏လက္ခဏာများ

ဖြစ်နိုင်ခြေသီအိုရီနှင့် စာရင်းဇယားများနှင့်ဆက်စပ်သော Pareto ဖြန့်ဖြူးမှု၏ အရေးကြီးဆုံးလက္ခဏာများဖြစ်သည်။

  • Pareto ဖြန့်ဝေမှုတွင် ၎င်း၏မျဉ်းကွေးကို သတ်မှတ်သည့် လက္ခဏာရပ်နှစ်ခု ရှိသည်- စကေး ကန့်သတ်ဘောင် x m နှင့် ပုံသဏ္ဍာန် ဘောင် α။

X\sim \text{Pareto}(\alpha,x_m)

  • Pareto ဖြန့်ဖြူးမှု၏ဒိုမိန်းတွင် စကေးပါရာမီတာမှ အပေါင်း အနန္တအထိ ကိန်းဂဏာန်းများအားလုံး ပါဝင်ပါသည်။

x\in [x_m,+\infty)

  • α သည် 1 ထက် ကြီးပါက၊ Pareto ဖြန့်ဖြူးမှု၏ပျမ်းမျှသည် α အမြှောက် x m နှင့် α အနှုတ် 1 တို့၏ ထုတ်ကုန်နှင့် ညီမျှသည်။

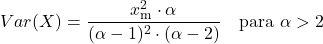
E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=” Rendered by QuickLaTeX.com” height=” 34″ width=” 214″ style=” vertical-align: -12px;” ></p> </p> <ul> <li> Pareto ဖြန့်ဖြူးမှု၏ကွဲလွဲမှုသည် ဖြန့်ဖြူးမှု၏ဝိသေသဘောင်နှစ်ခုအပေါ် မူတည်ပြီး အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-</li> </ul> <p class=\displaystyle Var(X)=\frac{x_\mathrm{m}^2\cdot \alpha}{(\alpha-1)^2\cdot(\alpha-2)}\quad \text{para }\alpha>2″ title=” Rendered by QuickLaTeX.com” height=” 44″ width=” 323″ style=” vertical-align: -17px;” ></p> </p> <ul> <li> Pareto ဖြန့်ဖြူးမှု၏ ပျမ်းမျှအား အောက်ပါစကားရပ်ဖြင့် ဆုံးဖြတ်နိုင်ပါသည်။</li> </ul> <p class=\displaystyle Me=x_\mathrm{m}\cdot \sqrt[\alpha]{2}

  • Pareto ဖြန့်ဖြူးမှု၏မုဒ်သည် ဖြန့်ဖြူးမှု၏ စကေးပါရာမီတာ x m နှင့် ညီမျှသည်။

Mo=x_m

  • Pareto ဖြန့်ဖြူးမှု၏ သိပ်သည်းဆလုပ်ဆောင်မှုအတွက် ဖော်မြူလာမှာ-

\displaystyle P[X=x]=\frac{\alpha\cdot x_m^\alpha}{x^{\alpha+1}}\quad\text{para }x\geq x_m

  • အလားတူပင်၊ Pareto ဖြန့်ဖြူးမှု၏ တိုးပွားလာနိုင်သော ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်အတွက် ဖော်မြူလာမှာ-

\displaystyle P[X\leq x]=1-\left(\frac{x_\mathrm{m}}{x}\right)^\alpha

  • Pareto ဖြန့်ဖြူးမှု၏ အချိုးမညီသောကိန်းဂဏန်းသည် ပုံသဏ္ဍာန်ဘောင် α ပေါ်တွင်သာ မူတည်ပြီး ၎င်း၏ဖော်ပြချက်မှာ-

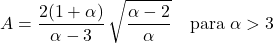
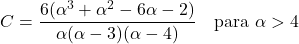
\displaystyle A=\frac{2(1+\alpha)}{\alpha-3}\,\sqrt{\frac{\alpha-2}{\alpha}}\quad\text{para }\alpha>3″ title=” Rendered by QuickLaTeX.com” height=” 43″ width=” 274″ style=” vertical-align: -14px;” ></p> </p> <ul> <li> Pareto ဖြန့်ဖြူးမှု၏ kurtosis ကိန်းဂဏန်းသည် α ဘောင်တန်ဖိုးပေါ်မူတည်၍ ကွဲပြားပြီး အောက်ပါဖော်မြူလာကို အသုံးပြု၍ တွက်ချက်သည်-</li> </ul> <p class=\displaystyle C=\frac{6(\alpha^3+\alpha^2-6\alpha-2)}{\alpha(\alpha-3)(\alpha-4)}\quad\text{para }\alpha>4″ title=” Rendered by QuickLaTeX.com” height=” 44″ width=” 299″ style=” vertical-align: -17px;” ></p></p> </div><!-- End Content --> <!-- Start Author Box --> <div class=

စာရေးသူအကြောင်း

Benjamin Anderson
Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

မှတ်ချက်တစ်ခုထည့်ပါ။

သင့် email လိပ်စာကို ဖော်ပြမည် မဟုတ်ပါ။ လိုအပ်သော ကွက်လပ်များကို * ဖြင့်မှတ်သားထားသည်