Excel တွင် partial f test ဖြေဆိုနည်း
တစ်စိတ်တစ်ပိုင်း F-test ကို regression model နှင့် တူညီသော model ၏ nested ဗားရှင်းကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ရှိမရှိ ဆုံးဖြတ်ရန် အသုံးပြုပါသည်။
nested model သည် ယေဘုယျအားဖြင့် regression model တွင် ကြိုတင်ခန့်မှန်းနိုင်သော variable အစုအဝေးတစ်ခုပါရှိသော မော်ဒယ်တစ်ခုဖြစ်သည်။
ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် ကြိုတင်ခန့်မှန်းကိန်းရှင် လေးခုပါရှိသော အောက်ဖော်ပြပါ ဆုတ်ယုတ်မှုပုံစံ ရှိသည်ဆိုပါစို့။
Y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4 + ε
nested model ၏နမူနာတစ်ခုသည် မူရင်းကြိုတင်ခန့်မှန်းကိန်းရှင်နှစ်ခုသာပါရှိသော အောက်ပါမော်ဒယ်ဖြစ်လိမ့်မည်-
Y = β 0 + β 1 x 1 + β 2 x 2 + ε
ဤမော်ဒယ်နှစ်ခုသည် သိသာထင်ရှားစွာ ခြားနားမှုရှိမရှိ ဆုံးဖြတ်ရန်၊ အောက်ပါ F-test ကိန်းဂဏန်းကို တွက်ချက်သည့် တစ်စိတ်တစ်ပိုင်း F-test ကို လုပ်ဆောင်နိုင်သည်-
F = (( RSS လျှော့ချထားသည် – Full RSS)/p) / ( RSS အပြည့်အစုံ /nk )
ရွှေ-
- လျှော့ချထားသော RSS − လျှော့ထားသော (ဆိုလိုသည်မှာ “nested”) မော်ဒယ်၏ လေးထောင့်အကျန်များ။
- RSS full : မော်ဒယ်အပြည့်၏ ကျန်ရှိသော ပေါင်းလဒ်။
- p- မော်ဒယ်အပြည့်အစုံမှ ကြိုတင်ခန့်မှန်းသူအရေအတွက်ကို ဖယ်ရှားထားသည်။
- n- ဒေတာအတွဲတွင် ကြည့်ရှုမှုစုစုပေါင်း။
- k- မော်ဒယ်အပြည့်အစုံရှိ ကိန်းဂဏန်းများ (ကြားဖြတ်စနစ် အပါအဝင်)။
ဤစမ်းသပ်မှုသည် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြုသည် ။
H 0 : မော်ဒယ်အပြည့်မှ ဖယ်ထားသော coefficient အားလုံးသည် သုညဖြစ်သည်။
H A : ပြီးပြည့်စုံသော မော်ဒယ်မှ ဖယ်ရှားလိုက်သော ကိန်းဂဏန်းများထဲမှ အနည်းဆုံးတစ်ခုသည် သုညမဟုတ်ပေ။
F-test ကိန်းဂဏန်းနှင့် သက်ဆိုင်သော p-value သည် အချို့သော အရေးပါမှုအဆင့် (ဥပမာ- 0.05) အောက်တွင် ရှိနေပါက၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်နိုင်ပြီး မော်ဒယ်အပြည့်မှ ဖယ်ထားသော အနည်းဆုံး coefficients များထဲမှ တစ်ခုသည် သိသာထင်ရှားသည်ဟု ကောက်ချက်ချနိုင်ပါသည်။
အောက်ဖော်ပြပါ ဥပမာသည် Excel တွင် တစ်စိတ်တစ်ပိုင်း F စာမေးပွဲကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသထားသည်။
ဥပမာ- Excel တွင် တစ်စိတ်တစ်ပိုင်း F စမ်းသပ်မှု
Excel တွင်အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။
အောက်ဖော်ပြပါ ဆုတ်ယုတ်မှုပုံစံနှစ်ခုကြား ခြားနားချက်ရှိမရှိ ဆုံးဖြတ်လိုသည်ဆိုပါစို့။
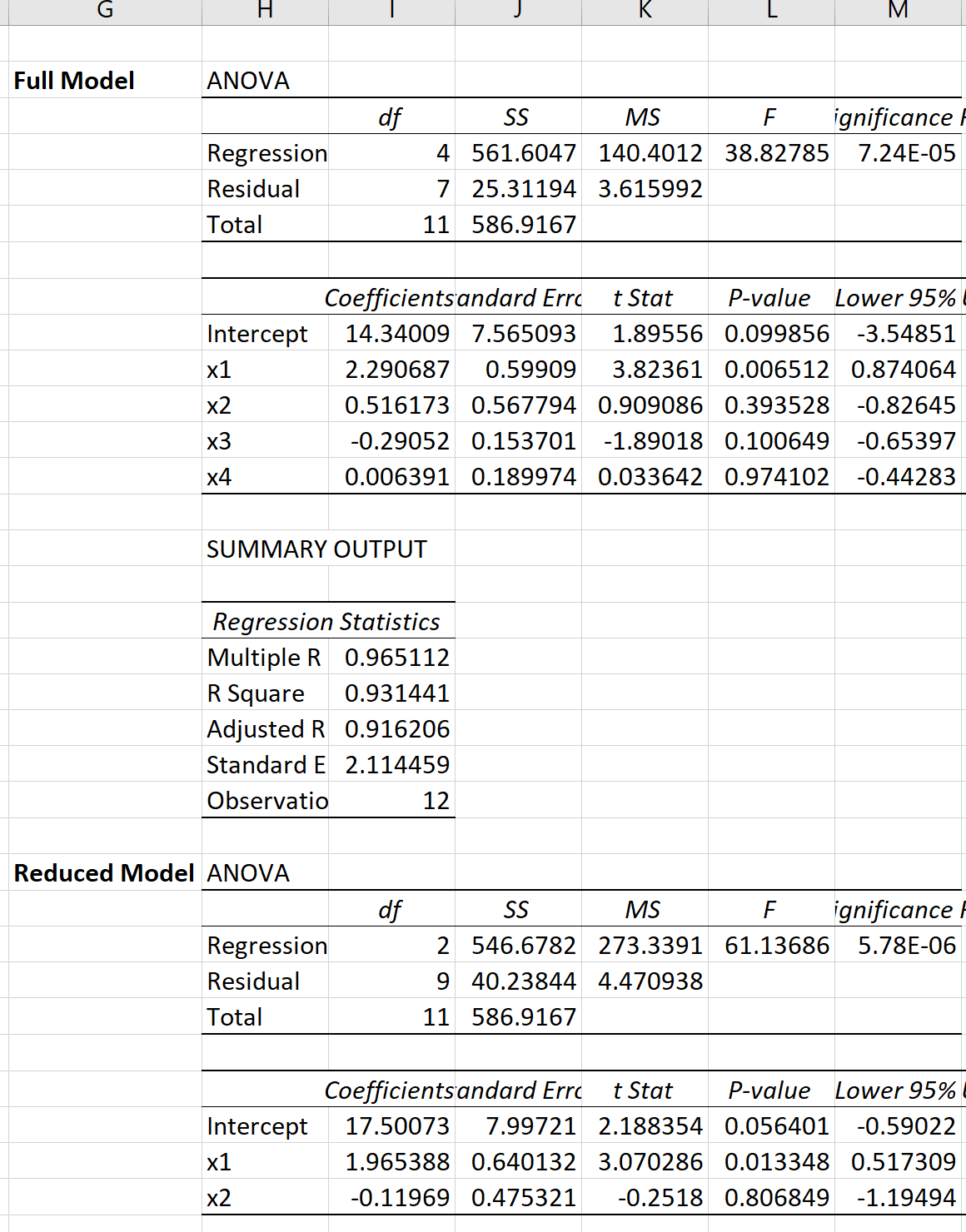
မော်ဒယ်အပြည့်အစုံ- y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4
လျှော့ချထားသော မော်ဒယ်- y = β 0 + β 1 x 1 + β 2 x 2
အောက်ဖော်ပြပါရလဒ်ရရှိရန် မော်ဒယ်တစ်ခုစီအတွက် Excel တွင် မျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှုများစွာကို လုပ်ဆောင်နိုင်သည်-
ထို့နောက် တစ်စိတ်တစ်ပိုင်း F-test အတွက် F-test ကိန်းဂဏန်းကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို အသုံးပြုနိုင်ပါသည်။
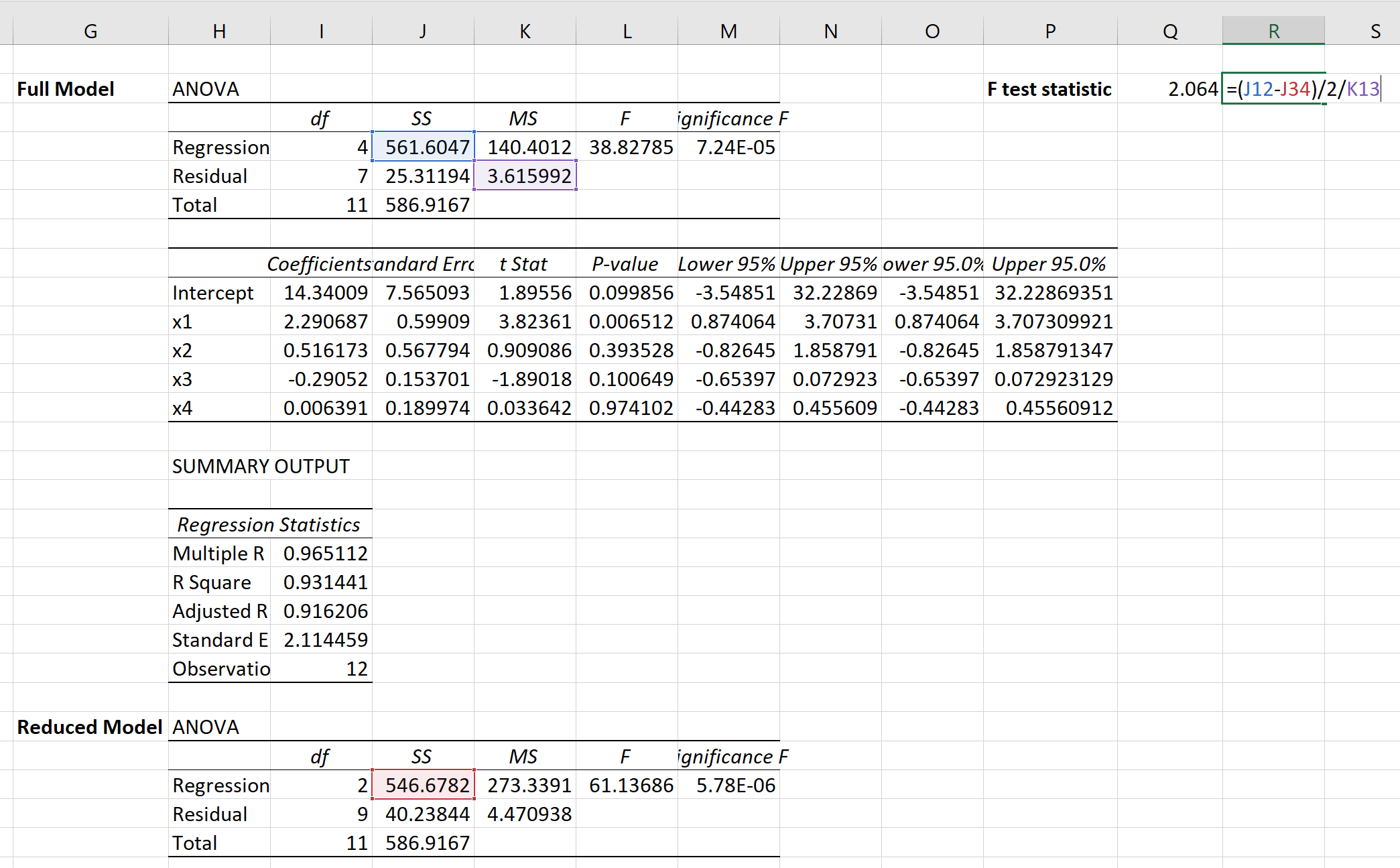
စမ်းသပ်မှုစာရင်းအင်းသည် 2.064 ဖြစ်လာသည်။
ထို့နောက် သက်ဆိုင်ရာ p-value ကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို အသုံးပြုနိုင်ပါသည်။
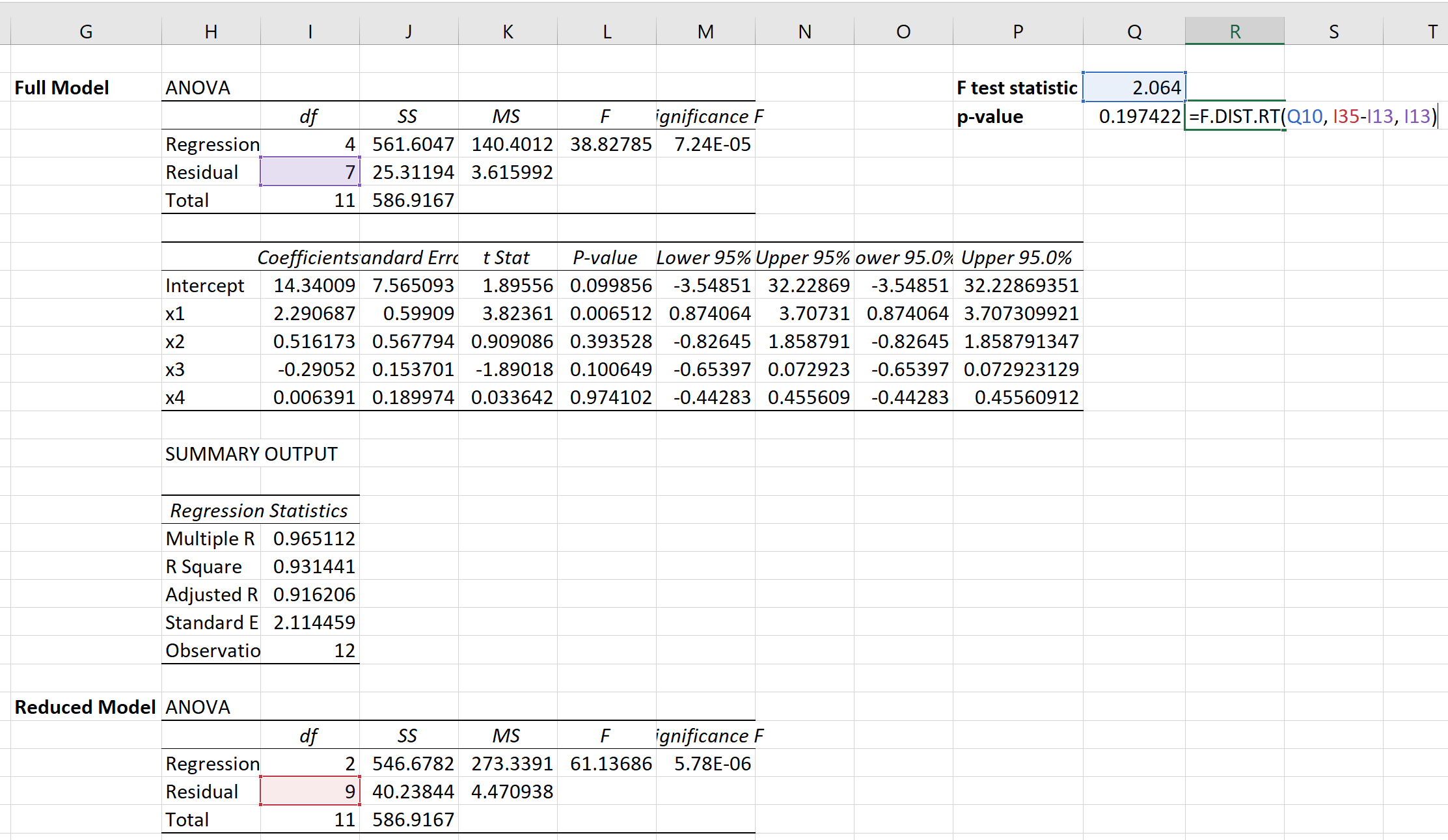
p-value သည် 0.1974 ဖြစ်သည် ။
ဤ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်မည်မဟုတ်ပါ။ ဆိုလိုသည်မှာ x3 သို့မဟုတ် x4 ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်များသည် စာရင်းအင်းအရ သိသာထင်ရှားသည်ဟုဆိုရန် ကျွန်ုပ်တို့တွင် လုံလောက်သောအထောက်အထားမရှိပါ။
တစ်နည်းဆိုရသော်၊ x3 နှင့် x4 ကို regression model သို့ ပေါင်းထည့်ခြင်းသည် model fit ကို သိသိသာသာ တိုးတက်စေခြင်း မရှိပါ။
ထပ်လောင်းအရင်းအမြစ်များ
Excel တွင် ရိုးရှင်းသော linear regression လုပ်နည်း
Excel တွင် linear regression အများအပြားလုပ်ဆောင်နည်း
Excel တွင် Regression ၏ Standard Error တွက်ချက်နည်း
စာရေးသူအကြောင်း
Benjamin Anderson
မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။