Pearson correlation coefficient

Pearson ဆက်စပ်ဆက်စပ်ကိန်း (“ထုတ်ကုန်-အခိုက်အတန့်ဆက်စပ်ကိန်း) သည် ကိန်းရှင် X နှင့် Y နှစ်ခုကြားရှိ မျဉ်းကြောင်းဆက်စပ်မှုဆိုင်ရာ တိုင်းတာမှုတစ်ခုဖြစ်သည်။ ၎င်းတွင် -1 နှင့် 1 အကြားတန်ဖိုးရှိသည်-

• -1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပျက်သဘောဆောင်သော ဆက်စပ်ဆက်နွယ်မှုကို ညွှန်ပြသည်။
• 0 သည် variable နှစ်ခုကြားတွင် linear ဆက်စပ်မှုမရှိဟု ညွှန်ပြသည်။
• 1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပြုသဘောဆောင်သောမျဉ်းကြောင်းဆက်စပ်မှုကို ညွှန်ပြသည်။

Pearson ဆက်စပ်ကိန်းကို ရှာဖွေခြင်းအတွက် ဖော်မြူလာ

ဒေတာနမူနာအတွက် Pearson ဆက်စပ်ဆက်စပ်ကိန်းကို ရှာဖွေရန် ဖော်မြူလာမှာ ( Wikipedia မှတဆင့် ):

သင့်အတွက် ဆော့ဖ်ဝဲလ်ကိုသုံးနိုင်သောကြောင့် ဤဖော်မြူလာကို သင်ဘယ်သောအခါမှ တွက်ချက်ရလိမ့်မည်မဟုတ်သော်လည်း၊ ဥပမာတစ်ခုအားဖြင့် ဤဖော်မြူလာ၏အတိအကျလုပ်ဆောင်ပုံကို နားလည်ရန် အထောက်အကူဖြစ်စေပါသည်။

ကျွန်ုပ်တို့တွင် အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။

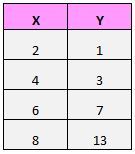
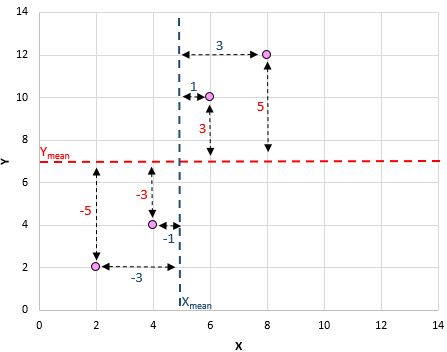
အကယ်၍ ကျွန်ုပ်တို့သည် ဤအတွဲများ (X၊ Y) ကို အကွဲအပြဲတစ်ခုတွင် ပုံဖော်ပါက၊ ၎င်းသည် ဤကဲ့သို့ ဖြစ်လိမ့်မည်-

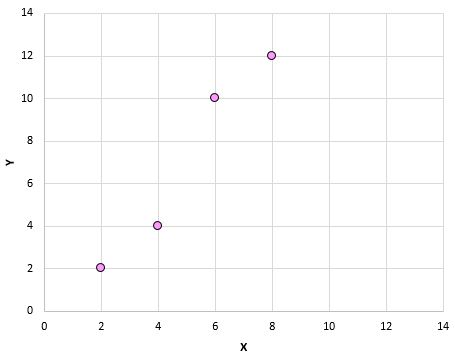
ဤအပိုင်းအစကို ကြည့်ခြင်းဖြင့်၊ X နှင့် Y သည် ကိန်းရှင်များအကြား အပြုသဘောဆောင်သော ဆက်နွယ်မှုရှိကြောင်း ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်- X တိုးလာသည်နှင့်အမျှ Y လည်း တိုးလာပါသည်။ သို့သော် ဤကိန်းရှင်နှစ်ခုသည် မည်မျှအကောင်းဘက်က ဆက်စပ်နေကြောင်း အတိအကျ တွက်ချက်ရန်အတွက် Pearson ဆက်စပ်ကိန်းကို ရှာဖွေရန် လိုအပ်ပါသည်။

ဖော်မြူလာ၏ ပိုင်းဝေကို အာရုံစိုက်ကြည့်ကြပါစို့။

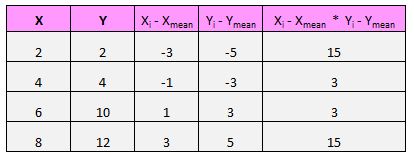
ကျွန်ုပ်တို့၏ဒေတာအတွဲတစ်ခုစီတွင် (X၊ Y) အတွဲတစ်ခုစီအတွက်၊ ကျွန်ုပ်တို့သည် x တန်ဖိုးနှင့် ပျမ်းမျှ x တန်ဖိုးကြားခြားနားချက်၊ y တန်ဖိုးနှင့် ပျမ်းမျှ y တန်ဖိုးကြားခြားနားချက်ကို ရှာဖွေပြီးနောက် ဤဂဏန်းနှစ်လုံးကို ပေါင်းထည့်ရန် လိုအပ်သည်။

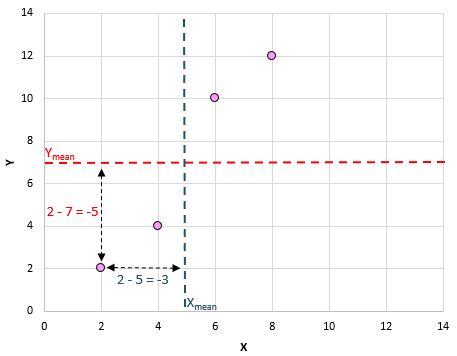
ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့၏ပထမတွဲ (X၊ Y) သည် (၂၊ ၂) ဖြစ်သည်။ ဤဒေတာအတွဲတွင် x ၏ ပျမ်းမျှတန်ဖိုးသည် 5 ဖြစ်ပြီး ဤဒေတာအတွဲရှိ y ၏ပျမ်းမျှတန်ဖိုးမှာ 7 ဖြစ်သည်။ ထို့ကြောင့် ဤအတွဲ၏ x တန်ဖိုးနှင့် x ၏ပျမ်းမျှတန်ဖိုးကြားကွာခြားချက်မှာ 2 – 5 = -3 ဖြစ်သည်။ ဤအတွဲ၏ y တန်ဖိုးနှင့် ပျမ်းမျှ y တန်ဖိုးကြား ကွာခြားချက်မှာ 2 – 7 = -5 ဖြစ်သည်။ အဲဒီ့ဂဏန်းနှစ်လုံးကို မြှောက်လိုက်တဲ့အခါ -3*-5=15 ကိုရသွားတယ်။

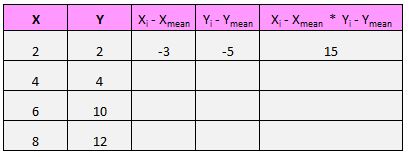
ဤသည်မှာ ကျွန်ုပ်တို့လုပ်ခဲ့သည့်အရာများ၏ အမြင်အာရုံ ခြုံငုံသုံးသပ်ချက်ဖြစ်သည်-

ပြီးရင် အတွဲတစ်ခုစီအတွက် ဒါကိုလုပ်ပါ။

ဖော်မြူလာ၏ ပိုင်းဝေကို ရရှိရန် နောက်ဆုံးအဆင့်မှာ ဤတန်ဖိုးများအားလုံးကို ပေါင်းထည့်ရန်ဖြစ်သည်-

15 + 3 +3 + 15 = 36

ထို့နောက် ဖော်မြူလာ၏ ပိုင်းခြေသည် x နှင့် y အတွက် နှစ်ထပ်ကိန်း ကွဲလွဲချက်အားလုံး၏ ပေါင်းလဒ်ကို ရှာရန် ၊ ထို့နောက် ဤဂဏန်းနှစ်လုံးကို ပေါင်း၍ နှစ်ထပ်ကိန်းကို ယူပါ-

ထို့ကြောင့် x နှင့် y အတွက် ကွဲပြားမှုများ၏ လေးထပ်၏ ပေါင်းလဒ်ကို ဦးစွာ ရှာတွေ့ပါမည်။

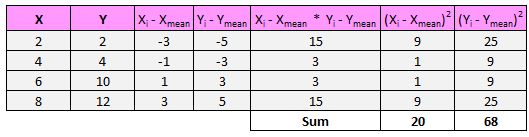
ထို့နောက်၊ ဤဂဏန်းနှစ်လုံးကို ပေါင်းမည်- 20*68 = 1,360။

နောက်ဆုံး၊ ကျွန်ုပ်တို့သည် နှစ်ထပ်ကိန်း- √ 1,360 = 36.88 ကို ယူပါမည်။

ထို့ကြောင့် ဖော်မြူလာ၏ ပိုင်းဝေသည် 36 ဖြစ်ပြီး ပိုင်းခြေမှာ 36.88 ဖြစ်ကြောင်း တွေ့ရှိရပါသည်။ ဆိုလိုသည်မှာ ကျွန်ုပ်တို့၏ Pearson ဆက်စပ်ကိန်းသည် r = 36 / 36.88 = 0.976 ဖြစ်သည်၊

ကျွန်ုပ်တို့၏ကိန်းရှင် X နှင့် Y အကြား ခိုင်မာသော အပြုသဘောဆောင်သော မျဉ်းရိုးဆက်နွယ်မှုရှိကြောင်း ညွှန်ပြသော ဤနံပါတ်သည် 1 နှင့် နီးစပ်ပါသည်။ ၎င်းသည် အပိုင်းအစတွင် ကျွန်ုပ်တို့လေ့လာတွေ့ရှိခဲ့သော ဆက်ဆံရေးကို အတည်ပြုသည်။

ဆက်စပ်မှုများကိုကြည့်ပါ။

Pearson ဆက်စပ်ဆက်စပ်ကိန်းက ကိန်းရှင်နှစ်ခုကြားရှိ မျဉ်းရိုးဆက်နွယ်မှု အမျိုးအစား (အပြုသဘော၊ အနုတ်လက္ခဏာ၊ မရှိ) နှင့် ဤဆက်ဆံရေး၏ ခွန်အား (အားနည်း၊ အလယ်အလတ်၊ အားကောင်း) ကို ပြောပြသည်ကို သတိရပါ။

variable နှစ်ခု၏ scatterplot တစ်ခုကို ဖန်တီးသောအခါ၊ variable နှစ်ခုကြားရှိ စစ်မှန်သော ဆက်နွယ်မှုကို ကျွန်ုပ်တို့ မြင်တွေ့ နိုင်သည်။ ဤသည်မှာ ကျွန်ုပ်တို့ သတိပြုမိနိုင်သော မျဉ်းဖြောင့် ဆက်ဆံရေး အမျိုးအစားများစွာ ဖြစ်သည်-

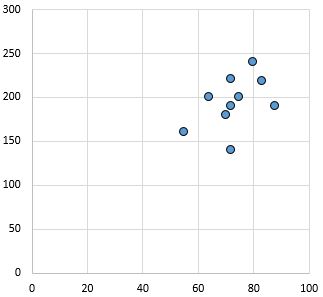
ခိုင်မာပြီး အပြုသဘောဆောင်သော ဆက်ဆံရေး- x-axis ပေါ်ရှိ ကိန်းရှင် တိုးလာသည်နှင့်အမျှ y-ဝင်ရိုးပေါ်ရှိ ကိန်းရှင်သည်လည်း တိုးလာပါသည်။ အချက်များကို အနီးကပ် အစုလိုက်အပြုံလိုက် စုစည်းထားပြီး ခိုင်မာသော ဆက်ဆံရေးကို ညွှန်ပြသည်။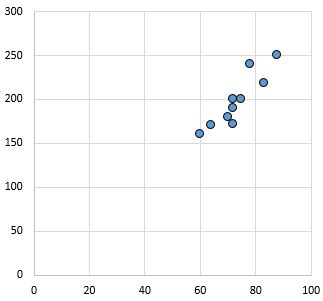

Pearson ဆက်စပ်ကိန်းဂဏန်း- 0.94

အားနည်းပြီး အပြုသဘောဆောင်သော ဆက်ဆံရေး- x-axis ပေါ်ရှိ ကိန်းရှင်များ တိုးလာသည်နှင့်အမျှ y-ဝင်ရိုးပေါ်ရှိ ကိန်းရှင်သည်လည်း တိုးလာပါသည်။ အချက်များသည် ကွဲလွဲနေပြီး ဆက်ဆံရေး အားနည်းမှုကို ညွှန်ပြနေသည်။

Pearson ဆက်စပ်ကိန်းဂဏန်း- 0.44

ဆက်ဆံရေးမရှိခြင်း- ကိန်းရှင်များကြားတွင် ရှင်းလင်းပြတ်သားသော ဆက်ဆံရေး (အပြုသဘော သို့မဟုတ် အနုတ်လက္ခဏာ) မရှိပါ။

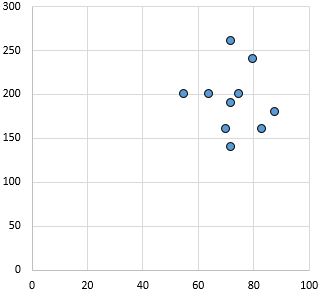
Pearson ဆက်စပ်ကိန်းဂဏန်း- 0.03

ခိုင်ခံ့သော၊ အပျက်သဘောဆောင်သော ဆက်ဆံရေး- x-axis ပေါ်ရှိ ကိန်းရှင် တိုးလာသည်နှင့်အမျှ y-ဝင်ရိုးပေါ်ရှိ ကိန်းရှင်သည် လျော့နည်းသွားသည်။ အချက်များသည် ခိုင်မာသော ဆက်ဆံရေးကို ညွှန်ပြနေပါသည်။

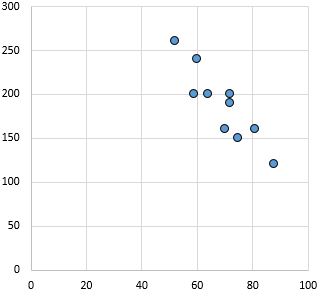
Pearson ဆက်စပ်ဖော်ကိန်း- -0.87

အားနည်းခြင်းနှင့် အနုတ်လက္ခဏာ ဆက်ဆံရေး- x-axis ပေါ်ရှိ ကိန်းရှင်များ တိုးလာသည်နှင့်အမျှ y-ဝင်ရိုးပေါ်ရှိ ကိန်းရှင်သည် လျော့နည်းသွားပါသည်။ အချက်များသည် ကွဲလွဲနေပြီး ဆက်ဆံရေး အားနည်းမှုကို ညွှန်ပြနေသည်။

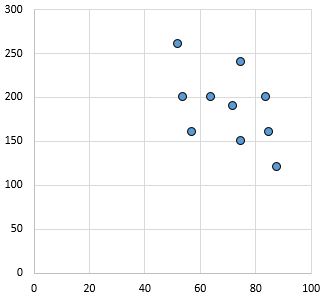
Pearson ဆက်စပ်ဆက်စပ်ကိန်း- 0.46

Pearson ဆက်စပ်ကိန်း၏ အရေးပါမှုကို စမ်းသပ်ခြင်း။

ဒေတာအစုတစ်ခုအတွက် Pearson ဆက်စပ်ကိန်းကို ကျွန်ုပ်တို့ရှာဖွေသောအခါ၊ ကျွန်ုပ်တို့သည် များပြားသော လူဦးရေ ထံမှ ဒေတာ နမူနာ တစ်ခုဖြင့် လုပ်ဆောင်လေ့ရှိသည်။ ဆိုလိုသည်မှာ ၎င်းတို့သည် စုစုပေါင်းလူဦးရေတွင် အမှန်တကယ် ဆက်စပ်မှုမရှိသော်လည်း ကိန်းရှင်နှစ်ခုအတွက် သုညမဟုတ်သော ဆက်စပ်မှုကို ရှာတွေ့နိုင်သည်ဟု ဆိုလိုသည်။

ဥပမာအားဖြင့်၊ လူဦးရေတစ်ခုလုံးရှိ data point တစ်ခုစီအတွက် variable X နှင့် Y အတွက် scatterplot တစ်ခုကို ဖန်တီးထားသည်ဆိုပါစို့။

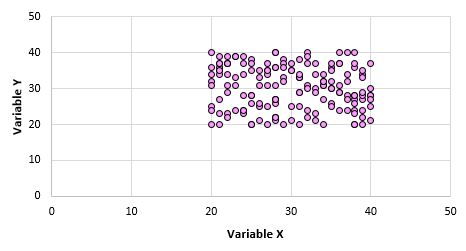
ဤကိန်းရှင်နှစ်ခုသည် ဆက်စပ်မှုမရှိသည်မှာ ထင်ရှားပါသည်။ သို့သော် လူဦးရေထံမှ 10 မှတ်နမူနာယူသောအခါတွင် အောက်ပါအချက်များကို ရွေးချယ်နိုင်သည်-

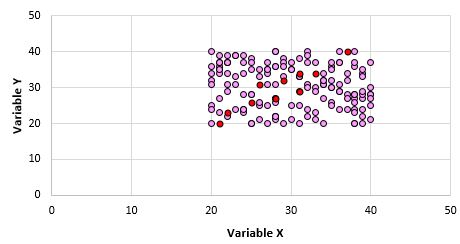
ဤနမူနာအတွက် အမှတ်များအတွက် Pearson ဆက်စပ်ကိန်းဂဏန်းသည် 0.93 ဖြစ်ပြီး လူဦးရေဆက်စပ်မှုမှာ သုညဖြစ်သော်လည်း ခိုင်မာသောအပြုသဘောဆက်စပ်ဆက်စပ်မှုကို ညွှန်ပြနေပါသည်။

ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်ဆက်နွှယ်မှုကို ကိန်းဂဏန်းအရ သိသာထင်ရှားမှုရှိမရှိ စမ်းသပ်ရန်အတွက်၊ ကျွန်ုပ်တို့သည် အောက်ပါစမ်းသပ်စာရင်းအင်းကို ရှာဖွေနိုင်သည်-

စမ်းသပ်စာရင်းအင်း T = r * √ (n-2) / (1-r ² )

ကျွန်ုပ်တို့နမူနာတွင် n သည် အတွဲအရေအတွက်ဖြစ်ပြီး၊ r သည် Pearson ဆက်စပ်ကိန်းဂဏန်းဖြစ်ပြီး T စမ်းသပ်မှုကိန်းဂဏန်းသည် လွတ်လပ်မှု n-2 ဒီဂရီဖြင့် ဖြန့်ဖြူးမှုကို လိုက်နာသည်။

Pearson ဆက်စပ်ကိန်း၏ အရေးပါပုံကို စမ်းသပ်နည်းနမူနာကို သုံးသပ်ကြည့်ကြပါစို့။

ဥပမာ

အောက်ပါဒေတာအတွဲသည် လူ ၁၂ ဦး၏ အရပ်နှင့် အလေးချိန်ကို ပြသသည်-

အောက်ပါ scatterplot သည် ဤကိန်းရှင်နှစ်ခု၏တန်ဖိုးကိုပြသသည်-

ဤကိန်းရှင်နှစ်ခုအတွက် Pearson ဆက်စပ်ဆက်စပ်ကိန်းသည် r = 0.836 ဖြစ်သည်။

စမ်းသပ်စာရင်းအင်း T = 0.836 * √ (12 -2) / (1-0.836 ² ) = 4.804 ။

ကျွန်ုပ်တို့၏ t ဖြန့်ချီရေးဂဏန်းတွက်စက်အရ ၊ လွတ်လပ်မှု 10 ဒီဂရီနှင့် ရမှတ် 4.804 တွင် p-value သည် 0.0007 ဖြစ်သည်။ 0.0007 < 0.05 မှစတင်၍ ဤဥပမာရှိ အလေးချိန်နှင့် အရပ်အမြင့်ကြားဆက်စပ်မှုသည် alpha = 0.05 တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသည်ဟု ကောက်ချက်ချနိုင်ပါသည်။

ကြိုတင်သတိပေးချက်များ

ကိန်းရှင်နှစ်ခုသည် မျဉ်းကြောင်းဆက်စပ်မှုရှိမရှိကို ပြောပြရာတွင် Pearson ဆက်စပ်ကိန်းက အသုံးဝင်နိုင်သော်လည်း Pearson ဆက်စပ်ကိန်းကို ဘာသာပြန်ဆိုရာတွင် အချက်သုံးချက်ကို မှတ်သားထားရန်လိုသည်-

1. ဆက်စပ်မှုသည် အကြောင်းရင်းကို မဆိုလိုပါ။ ကိန်းရှင်နှစ်ခုသည် တစ်ခုနှင့်တစ်ခု မကြာခဏဆိုသလို ပေါ်လာစေရန် သေချာပေါက် ဖြစ်စေသော ကိန်းရှင်နှစ်ခု ဆက်စပ်နေသောကြောင့် မဟုတ်ပါ။ ယင်း၏ ဂန္တဝင်ဥပမာတစ်ခုသည် ရေခဲမုန့်ရောင်းချမှုနှင့် ငါးမန်းတိုက်ခိုက်မှုကြားတွင် အပြုသဘောဆောင်သော ဆက်စပ်ဆက်နွယ်မှုဖြစ်သည်။ ယခုနှစ်၏အချို့သောအချိန်များတွင်ရေခဲမုန့်ရောင်းအားတိုးလာသောအခါ, ငါးမန်းတိုက်ခိုက်မှုလည်းတိုးတတ်သည်.

ရေခဲမုန့်စားခြင်းသည် ငါးမန်းတိုက်ခိုက်ခြင်းကို ဖြစ်စေသည် ဟု ဆိုလိုပါသလား။ ဘယ်ဟုတ်မလဲ! ရိုးရှင်းစွာဆိုလိုသည်မှာ နွေရာသီတွင် ရေခဲစားသုံးမှုနှင့် ငါးမန်းတိုက်ခိုက်မှုများ တိုးလာတတ်သည်ဟု ဆိုလိုသည်မှာ နွေရာသီတွင် ရေခဲသည် ပို၍ရေပန်းစားပြီး နွေရာသီတွင် သမုဒ္ဒရာထဲသို့ လူများပိုများလာသောကြောင့်ဖြစ်သည်။

2. ဆက်စပ်မှုများသည် အစွန်းအထင်းများအတွက် အကဲဆတ်သည်။ လွန်ကဲသော အပြင်ပန်းတစ်ခုသည် Pearson ဆက်စပ်ကိန်းကို သိသိသာသာ ပြောင်းလဲနိုင်သည်။ အောက်ပါ ဥပမာကို သုံးသပ်ကြည့်ပါ။

ကိန်းရှင် X နှင့် Y တွင် Pearson ဆက်စပ်ကိန်း 0.00 ရှိသည်။ သို့သော် ကျွန်ုပ်တို့တွင် ဒေတာအတွဲတွင် အကြမ်းဖျင်းတစ်ခုရှိသည်ကို မြင်ယောင်ကြည့်ပါ-

သို့သော် ဤကိန်းရှင်နှစ်ခုအတွက် Pearson ဆက်စပ်ကိန်းဂဏန်းသည် 0.878 ဖြစ်သည်။ ဒီအချက်က အရာအားလုံးကို ပြောင်းလဲစေတယ်။ ထို့ကြောင့်၊ variable နှစ်ခုအတွက် ဆက်စပ်မှုကို တွက်ချက်သောအခါ၊ outliers ကိုစစ်ဆေးရန် scatterplot ကိုအသုံးပြု၍ variable များကို မြင်သာစေရန် စိတ်ကူးကောင်းပါသည်။

3. Pearson ဆက်စပ်ဆက်စပ်ကိန်းသည် ကိန်းရှင်နှစ်ခုကြားတွင် လိုင်းမဟုတ်သော ဆက်ဆံရေးများကို မဖမ်းယူပါ။ အောက်ပါဆက်နွယ်မှုနှင့်အတူ ကျွန်ုပ်တို့တွင် ကိန်းရှင်နှစ်ခုရှိသည်ကို စိတ်ကူးကြည့်ကြပါစို့။

ဤကိန်းရှင်နှစ်ခုအတွက် Pearson ဆက်စပ်ဆက်စပ်ကိန်းသည် 0.00 ဖြစ်သောကြောင့် ၎င်းတို့တွင် မျဉ်းသားဆက်ဆံရေးမရှိသောကြောင့်ဖြစ်သည်။ သို့ရာတွင်၊ ဤကိန်းရှင်နှစ်ခုသည် မျဉ်းဖြောင့်မဟုတ်သော ဆက်နွယ်မှုရှိသည်။ y တန်ဖိုးများသည် ရိုးရိုး x တန်ဖိုးများ နှစ်ထပ်ကိန်းများဖြစ်သည်။

Pearson correlation coefficient ကိုအသုံးပြုသောအခါ၊ သင်သည် ကိန်းရှင်နှစ်ခုသည် မျဉ်းကြောင်း အတိုင်း ဆက်နွယ်မှုရှိမရှိကို ရိုးရိုးရှင်းရှင်း စမ်းသပ်နေကြောင်း သတိရပါ။ Pearson correlation coefficient သည် ကိန်းရှင်နှစ်ခုသည် ဆက်စပ်မှုမရှိဟု ကျွန်ုပ်တို့အားပြောပြသော်လည်း၊ ၎င်းတို့တွင် လိုင်းမဟုတ်သော ဆက်ဆံရေးအမျိုးအစားအချို့ ရှိသေးသည်။ ဤသည်မှာ ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်မှုကို ခွဲခြမ်းစိတ်ဖြာရာတွင် အပိုင်းခွဲတစ်ခုဖန်တီးရန် အသုံးဝင်သည့် အခြားအကြောင်းရင်းဖြစ်သည်- ၎င်းသည် သင့်အား linear မဟုတ်သော ဆက်ဆံရေးကို ရှာဖွေတွေ့ရှိရန် ကူညီပေးနိုင်ပါသည်။