Pearson correlation coefficient

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် Pearson ဆက်စပ်ဆက်စပ်ကိန်း (သို့မဟုတ် linear correlation coefficient) သည် အဘယ်အရာနှင့် ၎င်းကိုအသုံးပြုသည်ကို ရှင်းပြထားသည်။ အဆင့်ဆင့်လေ့ကျင့်ခန်းနှင့်အတူ Pearson ဆက်စပ်ကိန်းကို တွက်ချက်နည်းကို သင်ရှာဖွေတွေ့ရှိမည်ဖြစ်ပါသည်။ ထို့အပြင်၊ အဆုံးတွင် အွန်လိုင်းဂဏန်းတွက်စက်ဖြင့် မည်သည့်ဒေတာအတွဲ၏ Pearson Correlation Coefficient တန်ဖိုးကို သင်တွေ့နိုင်သည်။

Pearson ၏ ဆက်စပ်ကိန်း ဆိုသည်မှာ အဘယ်နည်း။

Pearson correlation coefficient သည် linear correlation coefficient သို့မဟုတ် ရိုးရှင်းသော correlation coefficient သည် ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်မှုကို ညွှန်ပြသည့် ကိန်းဂဏန်းဆိုင်ရာတိုင်းတာမှုတစ်ခုဖြစ်သည်။

ကိန်းရှင်နှစ်ခုကြားရှိ Pearson ဆက်စပ်ကိန်းကို တွက်ချက်ရန်၊ ၎င်းတို့ကွဲလွဲချက်များ၏ ထုတ်ကုန်၏ နှစ်ထပ်ကိန်းဖြင့် ပြောကြားထားသော ကိန်းရှင်များ၏ ကွဲလွဲမှုကို ပိုင်းခြားရပါမည်။

ထို့ကြောင့်၊ Pearson ဆက်စပ်ကိန်းဂဏန်းသည် ပမာဏကျပန်းကိန်းရှင်နှစ်ခုကြားရှိ မျဉ်းကြောင်းအတိုင်းမှီခိုမှုကို တွက်ချက်ရန် ကြိုးပမ်းသည်။ ဦးစားပေးတစ်ခု၊ ကိန်းရှင်များကြားဆက်စပ်မှုကို ကိန်းဂဏန်းများဖြင့်အကဲဖြတ်ရန်မှာ ကိန်းရှင်အတွဲများကြားတွင် ပိုမိုဆက်စပ်နေကြောင်း ဆုံးဖြတ်ရန်ခက်ခဲသောကြောင့် အကယ်၍ Pearson ၏ဆက်စပ်ကိန်း၏အရာဝတ္ထုသည် ကိန်းရှင်များကြားဆက်စပ်မှုကို တန်ဖိုးသတ်မှတ်ရန်ခက်ခဲသောကြောင့်ဖြစ်သည်။ သူတို့ကြားမှာ နှိုင်းယှဉ်ပါ။

Pearson ဆက်စပ်အညွှန်းကိန်း၏တန်ဖိုးသည် -1 နှင့် +1 အကြားတွင် ပါဝင်သည်။ Pearson correlation coefficient ၏တန်ဖိုးကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုသည်ကို အောက်တွင်ကြည့်ပါမည်။

Pearson Correlation Coefficient ဖော်မြူလာ

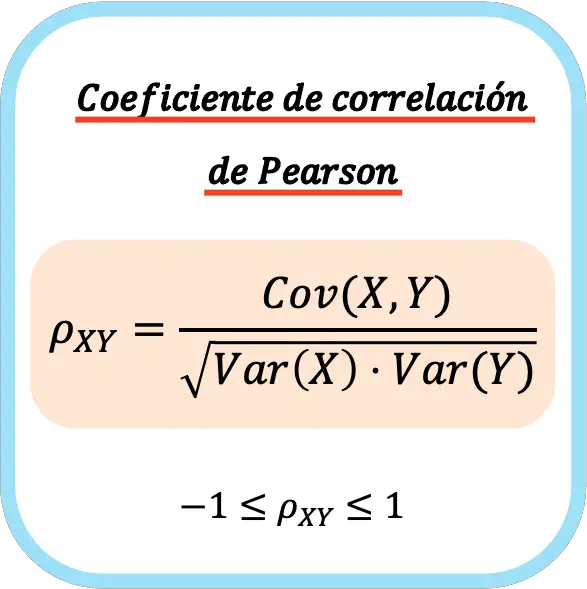
ကိန်းရှင်ကိန်းရှင်နှစ်ခု၏ Pearson ဆက်စပ်ဆက်စပ်ကိန်းသည် ကိန်းရှင်များ၏ကွဲလွဲချက်တစ်ခုစီ၏ကွဲလွဲမှုတစ်ခုစီ၏ကွဲလွဲမှု၏ထုတ်ကုန်၏နှစ်ထပ်ကိန်းကြားနှင့်ညီမျှသည်။

ထို့ကြောင့်၊ Pearson ဆက်စပ်ကိန်းကို တွက်ချက်ရန် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

Pearson correlation coefficient, linear correlation coefficient

👉 မည်သည့်ဒေတာအတွဲအတွက်မဆို Pearson ဆက်စပ်ကိန်းကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို အသုံးပြုနိုင်သည်။

လူဦးရေအပေါ် Pearson ဆက်စပ်ကိန်းကို တွက်ချက်သောအခါ၊ ယေဘုယျအားဖြင့် ဂရိအက္ခရာ ρ ဖြင့် ဖော်ပြသည်။ သို့သော် နမူနာတစ်ခုနှင့် ဆက်စပ်တွက်ချက်သော ကိန်းဂဏန်းအား r ကို သင်္ကေတအဖြစ် အသုံးပြုသည်။

Pearson ဆက်စပ်ကိန်းကို ဆုံးဖြတ်ရန်၊ variable နှစ်ခုနှင့် variable တစ်ခု၏ကွဲလွဲမှုကို တွက်ချက်နည်းကို သင်သိထားရန် လိုအပ်ကြောင်း သတိရပါ။ ထို့အပြင်၊ ဤစာရင်းအင်းဆိုင်ရာ အစီအမံများက ဘာကိုဆိုလိုသည်ကို နားလည်ရန် လိုအပ်ပါသည်။ ထို့ကြောင့် ရှင်းလင်းချက်ကို ဆက်လက်မလုပ်ဆောင်မီ အောက်ပါဆောင်းပါးနှစ်ခုကို ဖတ်ရန် အကြံပြုလိုသည်-

➤ ကွဲလွဲမှုကို တွက်ချက်နည်းကို ကြည့်ပါ။
➤ ကွာဟချက်ကို တွက်ချက်နည်းကို ကြည့်ပါ ။

Pearson ဆက်စပ်ကိန်းကို တွက်ချက်ခြင်း ဥပမာ

Pearson ၏ ဆက်စပ်ကိန်းကို အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်း၏ဖော်မြူလာကို ထည့်သွင်းစဉ်းစားခြင်းဖြင့်၊ အောက်တွင် အဆင့်ဆင့်သော ဥပမာတစ်ခုဖြစ်သောကြောင့် ၎င်းကို တွက်ချက်ပုံကို သင်ကြည့်ရှုနိုင်ပါသည်။

အောက်ပါ ဆက်တိုက်ကိန်းရှင်နှစ်ခုကြားရှိ Pearson ဆက်စပ်ကိန်းကို တွက်ချက်ပါ-

Pearson ဆက်စပ်ကိန်းကို မတွက်ချက်မီ၊ ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်မှုကို ပိုင်းခြားစိတ်ဖြာရန် ကျွန်ုပ်တို့သည် ဒေတာအတွဲကို ခွဲခြမ်းစိတ်ဖြာရန်အတွက် ဒေတာအတွဲကို ကိုယ်စားပြုပါမည်။

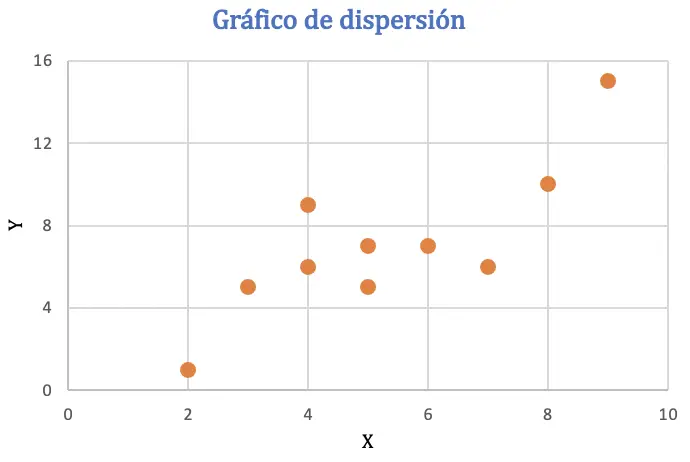
scatter plot မှ data သည် positive trend ဖြစ်နိုင်သည်၊ သို့မဟုတ် တနည်းအားဖြင့်၊ variable တစ်ခုသည် value တိုးလာသောအခါတွင် အခြားသော variable သည်လည်း တိုးလာသည်ဟု ကောက်ချက်ချနိုင်ပါသည်။ ဆက်စပ်မှုကို စစ်ဆေးရန်၊ Pearson coefficient ကို တွေ့ရပါမည်။

ပထမဆုံးလုပ်ရမှာက variable တစ်ခုစီရဲ့ ဂဏန်းသင်္ချာပျမ်းမျှကို သီးခြားစီရှာပြီး လေ့လာမှုအရေအတွက်နဲ့ ခွဲထားတဲ့ data စုစုပေါင်းပေါင်းလဒ်နဲ့ညီမျှပါတယ်။

$\overline{x}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}=\cfrac{53}{10}=5,3$

$\overline{y}=\cfrac{\displaystyle \sum_{i=1}^n y_i}{n}=\cfrac{71}{10}=7,1$

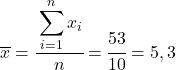
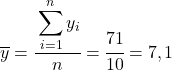
ယခု ကျွန်ုပ်တို့သည် ကိန်းရှင်တစ်ခုစီ၏ ဆိုလိုရင်းကို သိလာသောအခါ၊ ဒေတာဇယားတွင် အောက်ပါကော်လံများကို ထည့်ရန် လိုအပ်သည်-

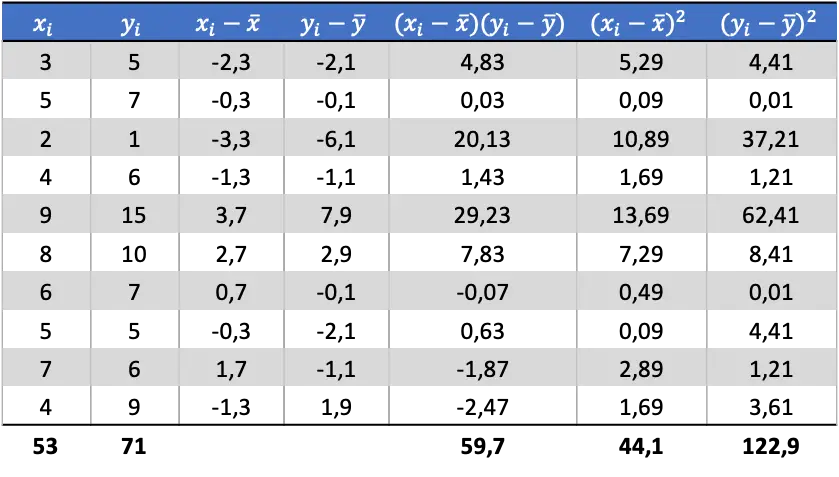
ဇယားရှိတွက်ချက်ထားသောဒေတာမှ၊ ကျွန်ုပ်တို့သည် ကွဲလွဲမှု နှင့် ကွဲလွဲမှုများ၏ တန်ဖိုးများကို ဆုံးဖြတ်သည် (၎င်းကို မည်သို့လုပ်ဆောင်ခဲ့သည်ကို မမှတ်မိပါက၊ ဤအရာအား အသေးစိတ်ရှင်းပြထားသည့် အထက်တွင် လင့်ခ်နှစ်ခုရှိသည်)။

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}=\cfrac{59,7}{10}=5,97$

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}=\cfrac{44,1}{10}=4,41$

$Var(Y)=\cfrac{\displaystyle\sum_{i=1}^n\left(y_i-\overline{y}\right)^2}{n}=\cfrac{122,9}{10}=12,29$

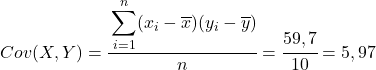
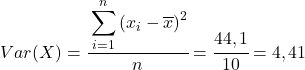
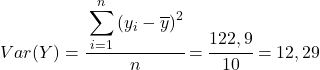
နောက်ဆုံးတွင်၊ ၎င်း၏တန်ဖိုးကိုရရှိရန် Pearson correlation coefficient ဖော်မြူလာကို ရိုးရှင်းစွာအသုံးပြုပါ-

$\rho_{XY}=\cfrac{Cov(X,Y)}{\sqrt{Var(X)\cdot Var(Y)}}=\cfrac{5,97}{\sqrt{4,41\cdot 12,29}}=0,81$

Pearson ဆက်စပ်ဆက်စပ်ကိန်းသည် 1 နှင့် အလွန်နီးစပ်သောတန်ဖိုးရှိသည်၊ ဆိုလိုသည်မှာ ဤကိန်းရှင်နှစ်ခုသည် အတော်အတန်ခိုင်မာသောအပြုသဘောဆက်စပ်မှုရှိသည်ဟု ဆိုလိုသည်။

သင်တွေ့မြင်ရသည့်အတိုင်း Pearson ဆက်စပ်ကိန်းကို ဆုံးဖြတ်ရန် ကော်လံတွက်ချက်မှုများကို ပိုမိုမြန်ဆန်စွာလုပ်ဆောင်ရန် Excel ကဲ့သို့သော ပရိုဂရမ်များကို အသုံးပြုခြင်းသည် အလွန်အသုံးဝင်ပါသည်။

Pearson Correlation Coefficient ဂဏန်းတွက်စက်

ကိန်းရှင်နှစ်ခုကြားရှိ Pearson ဆက်စပ်ကိန်းကို တွက်ချက်ရန် အောက်ပါဂဏန်းပေါင်းစက်ထဲသို့ ကိန်းဂဏန်းအချက်အလက်အစုတစ်စုကို ထည့်သွင်းပါ။ ဒေတာအတွဲများကို ခွဲခြားထားရန် လိုအပ်သည်၊ ထို့ကြောင့် ပထမအကွက်တွင် ကိန်းရှင်တစ်ခု၏ တန်ဖိုးများသာ ရှိပြီး ဒုတိယအကွက်တွင် ဒုတိယကိန်းရှင်၏ တန်ဖိုးများသာ ရှိနေမည်ဖြစ်သည်။

ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

Pearson Correlation Coefficient ကို ဘာသာပြန်ခြင်း။

၎င်း၏တန်ဖိုးကို သိရန် မလုံလောက်သောကြောင့် ၎င်းသည် Pearson ဆက်စပ်ကိန်းကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုရမည်ကို ဤအပိုင်းတွင် ကျွန်ုပ်တို့တွေ့မြင်ရမည်ဖြစ်ပြီး ၎င်း၏အဓိပ္ပာယ်ကို ခွဲခြမ်းစိတ်ဖြာနည်းကို သင်သိရမည်ဖြစ်သည်။

ထို့ကြောင့် Pearson ဆက်စပ်ကိန်းကို အနက်ဖွင့်ခြင်းသည် ၎င်း၏တန်ဖိုးပေါ်တွင် မူတည်သည်-

r=-1 : variable နှစ်ခုသည် ပြီးပြည့်စုံသော အနုတ်လက္ခဏာဆက်စပ်မှုရှိသည်၊ ထို့ကြောင့် အမှတ်အားလုံးချိတ်ဆက်သည့် negative slope ဖြင့်မျဉ်းကိုဆွဲနိုင်သည်။
-1<r<0 : variable နှစ်ခုကြား ဆက်စပ်မှုသည် အနှုတ်ဖြစ်ပြီး၊ ထို့ကြောင့် ကိန်းရှင်တစ်ခု တိုးလာသောအခါ အခြားတစ်ခု လျော့နည်းသွားသည်။ တန်ဖိုးသည် -1 နှင့် ပိုနီးစပ်လေ၊ ကိန်းရှင်များသည် အနုတ်လက္ခဏာနှင့် ဆက်စပ်လေလေဖြစ်သည်။
r=0 : variable နှစ်ခုကြား ဆက်စပ်မှုသည် အလွန်အားနည်းသည်၊ တကယ်တော့ ၎င်းတို့ကြားရှိ linear ဆက်ဆံရေးသည် သုညဖြစ်သည်။ ကိန်းရှင်များသည် အမှီအခိုကင်းသည်ဟု မဆိုလိုပါ၊ ၎င်းတို့သည် လိုင်းမဟုတ်သော ဆက်ဆံရေးရှိနိုင်သောကြောင့်ဖြစ်သည်။
0<r<1 : ကိန်းရှင်နှစ်ခုကြား ဆက်စပ်မှုသည် အပြုသဘောဖြစ်ပြီး၊ တန်ဖိုးသည် +1 နှင့် ပိုနီးစပ်လေ၊ ကိန်းရှင်များကြား ဆက်ဆံရေး အားကောင်းလေဖြစ်သည်။ ဤအခြေအနေမျိုးတွင်၊ အခြားတစ်ခုသည် တိုးလာသောအခါ ကိန်းရှင်တစ်ခုသည် တန်ဖိုးတက်လာတတ်သည်။
r=1 : ကိန်းရှင်နှစ်ခုသည် ပြီးပြည့်စုံသော အပြုသဘောဆက်စပ်ဆက်စပ်မှုရှိသည်၊ ဆိုလိုသည်မှာ ၎င်းတို့သည် အပြုသဘောဆောင်သောမျဉ်းကြောင်းဆိုင်ရာ ဆက်နွယ်မှုရှိသည်။

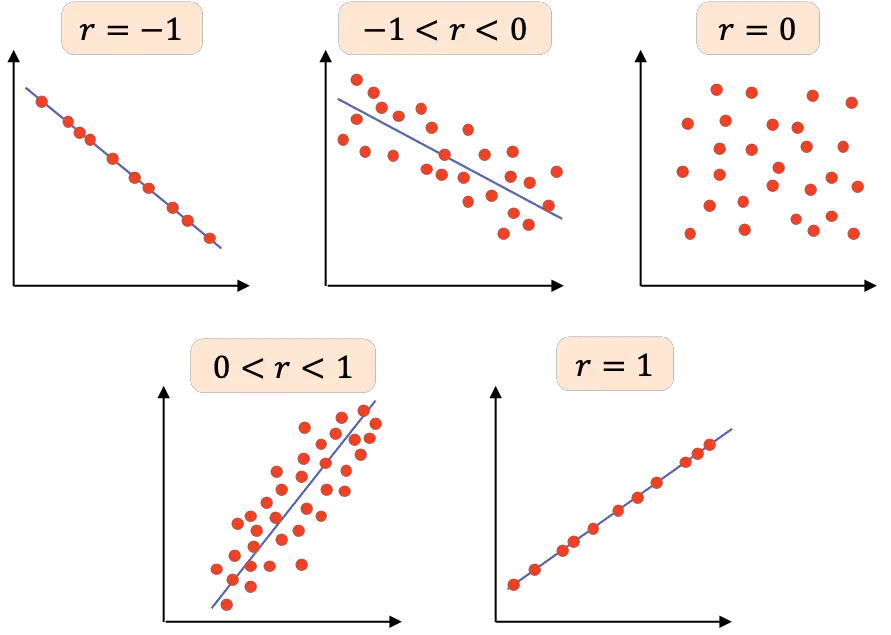
Pearson ဆက်စပ်ကိန်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်

အနှစ်ချုပ်အားဖြင့်၊ အောက်ပါဇယားကို Pearson ဆက်စပ်ဆက်စပ်ကိန်း၏ မတူညီသောအဓိပ္ပာယ်ဖွင့်ဆိုချက်များဖြင့် တင်ပြထားပါသည်။

တန်ဖိုး	စကားပြန်
r=-1	ပြီးပြည့်စုံသော အနုတ်လက္ခဏာဆက်စပ်မှု။
-1<r<0	အနုတ်လက္ခဏာဆက်စပ်ဆက်နွယ်မှု- ဆက်စပ်ဆက်နွယ်မှုသည် -1 နှင့်ပိုမိုနီးကပ်လေလေ၊ အားကောင်းလေဖြစ်သည်။
r=0	သုညမျဉ်းကြောင်းဆက်စပ်မှု။
0<r<၁	အပြုသဘောဆောင်သောဆက်စပ်ဆက်နွယ်မှု- ဆက်စပ်ဆက်နွယ်မှုသည် +1 နှင့်ပိုမိုနီးကပ်လေလေ၊ အားကောင်းလေဖြစ်သည်။
r=1	ပြီးပြည့်စုံသော အပြုသဘောဆက်စပ်မှု။

variable နှစ်ခုကြားတွင် ဆက်နွယ်မှုရှိလျှင်ပင် ၎င်းတို့ကြားတွင် အကြောင်းရင်းခံရှိနေသည်ဟု မဆိုလိုပါ ၊ ဆိုလိုသည်မှာ variable နှစ်ခုကြား ဆက်စပ်မှုသည် variable တစ်ခု၏ပြောင်းလဲမှုသည် variable ၏ပြောင်းလဲမှု၏အကြောင်းရင်းဖြစ်သည်ဟု မဆိုလိုပါ။ အခြားပြောင်းလဲမှု။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် ခန္ဓာကိုယ်အတွင်း မတူညီသော ဟော်မုန်းနှစ်မျိုး၏ ထုတ်လုပ်မှုကြားတွင် အပြုသဘောဆောင်သော ဆက်ဆံရေးရှိကြောင်း တွေ့ရှိပါက၊ ဟော်မုန်းတစ်ခု တိုးလာခြင်းသည် အခြားဟော်မုန်းတစ်ခု တိုးလာရန် မလိုအပ်ပါ။ ဖျားနာမှုကို တိုက်ဖျက်ရန် နှစ်မျိုးလုံးလိုအပ်သောကြောင့် ခန္ဓာကိုယ်မှ ဟော်မုန်းနှစ်မျိုးလုံးကို ထုတ်လုပ်နိုင်သောကြောင့် နှစ်မျိုးလုံး၏အဆင့်ကို တစ်ပြိုင်နက် တိုးမြင့်လာခြင်းကြောင့် ဖြစ်ရသည့်အကြောင်းရင်းမှာ ရောဂါဖြစ်နိုင်သည်။ ဟော်မုန်း နှစ်ခုကြား ဆက်စပ်မှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန်၊ နောက်ထပ် လေ့လာမှုများ ပြုလုပ်သင့်သည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။