Pearson ၏ဆက်စပ်မှု၏ယူဆချက်ငါးခု

Pearson ဆက်စပ်ဆက်စပ်ကိန်း (“ထုတ်ကုန်-အခိုက်အတန့်ဆက်နွှယ်မှုကိန်းဂဏန်း”) သည် ကိန်းရှင်နှစ်ခုကြားရှိ မျဉ်းသားဆက်စပ်မှုကို တိုင်းတာသည်။

၎င်းသည် အမြဲတမ်း -1 နှင့် 1 အကြား တန်ဖိုးတစ်ခုကို ယူသည်-

• -1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပျက်သဘောဆောင်သော ဆက်စပ်ဆက်နွယ်မှုကို ညွှန်ပြသည်။
• 0 သည် variable နှစ်ခုကြားတွင် linear ဆက်စပ်မှုမရှိဟု ညွှန်ပြသည်။
• 1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပြုသဘောဆောင်သောမျဉ်းကြောင်းဆက်စပ်မှုကို ညွှန်ပြသည်။

သို့သော်လည်း၊ ကိန်းရှင်နှစ်ခုကြားရှိ Pearson ဆက်စပ်ကိန်းကို မတွက်ချက်မီ၊ ယူဆချက်ငါးခုနှင့် ကိုက်ညီကြောင်း သေချာရပါမည်။

1. တိုင်းတာမှုအဆင့်- ကိန်းရှင်နှစ်ခုလုံးကို ကြားကာလ သို့မဟုတ် အချိုး အဆင့်တွင် တိုင်းတာသင့်သည်။

2. Linear ဆက်ဆံရေး- ကိန်းရှင်နှစ်ခုကြားတွင် linear ဆက်ဆံရေးရှိရမည်။

3. Normality- ကိန်းရှင်နှစ်ခုလုံးသည် ခန့်မှန်းခြေအားဖြင့် ပုံမှန်ဖြန့်ဖြူးမှုရှိသင့်သည်။

4. ဆက်စပ်အတွဲများ- ဒေတာအတွဲတွင် ကြည့်ရှုမှုတစ်ခုစီတွင် တန်ဖိုးတစ်စုံစီရှိရမည်။

5. အစွန်းထွက်များမရှိပါ- ဒေတာအစုံတွင် လွန်ကဲသောအစွန်းထွက်များ မရှိသင့်ပါ။

ဤဆောင်းပါးတွင်၊ ကျွန်ုပ်တို့သည် ယူဆချက်တစ်ခုစီ၏ ရှင်းလင်းချက်အပြင် ယူဆချက်နှင့်ကိုက်ညီခြင်းရှိမရှိကို မည်သို့ဆုံးဖြတ်ရမည်နည်း။

အယူအဆ 1- တိုင်းတာမှုအဆင့်

ကိန်းရှင်နှစ်ခုကြားရှိ Pearson ဆက်စပ်ကိန်းကို တွက်ချက်ရန်၊ ကိန်းရှင်နှစ်ခုလုံးကို ကြားကာလ သို့မဟုတ် အချိုး အဆင့်တွင် တိုင်းတာရပါမည်။

အောက်ဖော်ပြပါ ဂရပ်ဖစ်သည် ကိန်းရှင်များကို တိုင်းတာနိုင်သည့် အဆင့်လေးဆင့်ကို လျင်မြန်စွာ ရှင်းပြပေးသည်-

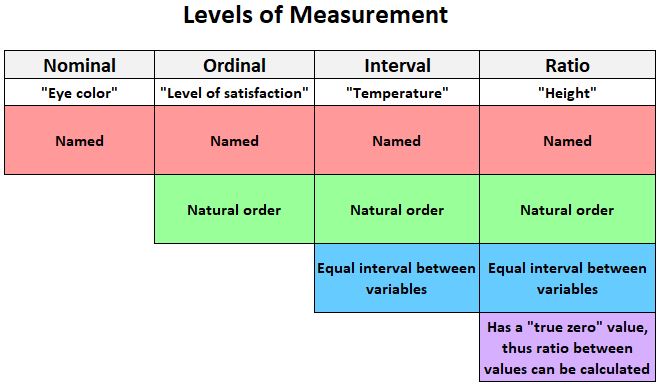
ဤသည်မှာ ကြားကာလ စကေးပေါ်တွင် တိုင်းတာနိုင်သော ကိန်းရှင်အချို့၏ ဥပမာများဖြစ်သည်။

• အပူချိန်- ဖာရင်ဟိုက် သို့မဟုတ် စင်တီဂရိတ်ဖြင့် တိုင်းတာသည်။
• ခရက်ဒစ်ရမှတ်များ- ၃၀၀ မှ ၈၅၀ အထိ တိုင်းတာသည်။
• SAT ရမှတ်များ- 400 မှ 1,600 အထိ တိုင်းတာသည်။

ဤသည်မှာ အချိုး စကေးပေါ်တွင် တိုင်းတာနိုင်သော ကိန်းရှင်အချို့၏ ဥပမာများဖြစ်သည်-

• အမြင့်- စင်တီမီတာ၊ လက်မ၊ ခြေ၊ စသည်ဖြင့် တိုင်းတာသည်။
• အလေးချိန်- ကီလိုဂရမ်၊ ပေါင် စသဖြင့် တိုင်းတာသည်။
• အရှည်- စင်တီမီတာ၊ လက်မ၊ ခြေ၊ စသည်တို့ဖြင့် တိုင်းတာသည်။

ကိန်းရှင်များကို သာမန် အဆင့်ဖြင့် တိုင်းတာပါက ၎င်းတို့ကြားရှိ Spearman ဆက်စပ်ကိန်းကို တွက်ချက်ရန် လိုအပ်သည်။

ဆက်စပ်- တိုင်းတာမှုအဆင့်များ- အမည်ခံ၊ ပုံမှန်၊ ကြားကာလနှင့် အချိုး

Hypothesis 2- Linear ဆက်ဆံရေး

ကိန်းရှင်နှစ်ခုကြားရှိ Pearson ဆက်စပ်ကိန်းကို တွက်ချက်ရန်၊ ကိန်းရှင်နှစ်ခုကြားတွင် မျဉ်းကြောင်းဆက်နွယ်မှုရှိရပါမည်။

ဤယူဆချက်အား စမ်းသပ်ရန် အလွယ်ကူဆုံးနည်းလမ်းမှာ ကိန်းရှင်နှစ်ခု၏ အပိုင်းအစတစ်ခုကို ဖန်တီးရန်ဖြစ်သည်။ ဇာတ်ကွက်ပေါ်ရှိ အမှတ်များသည် ခန့်မှန်းခြေအားဖြင့် မျဉ်းဖြောင့်အတိုင်း လိုက်ပါက၊ linear ဆက်နွယ်မှု ရှိနေသည်-

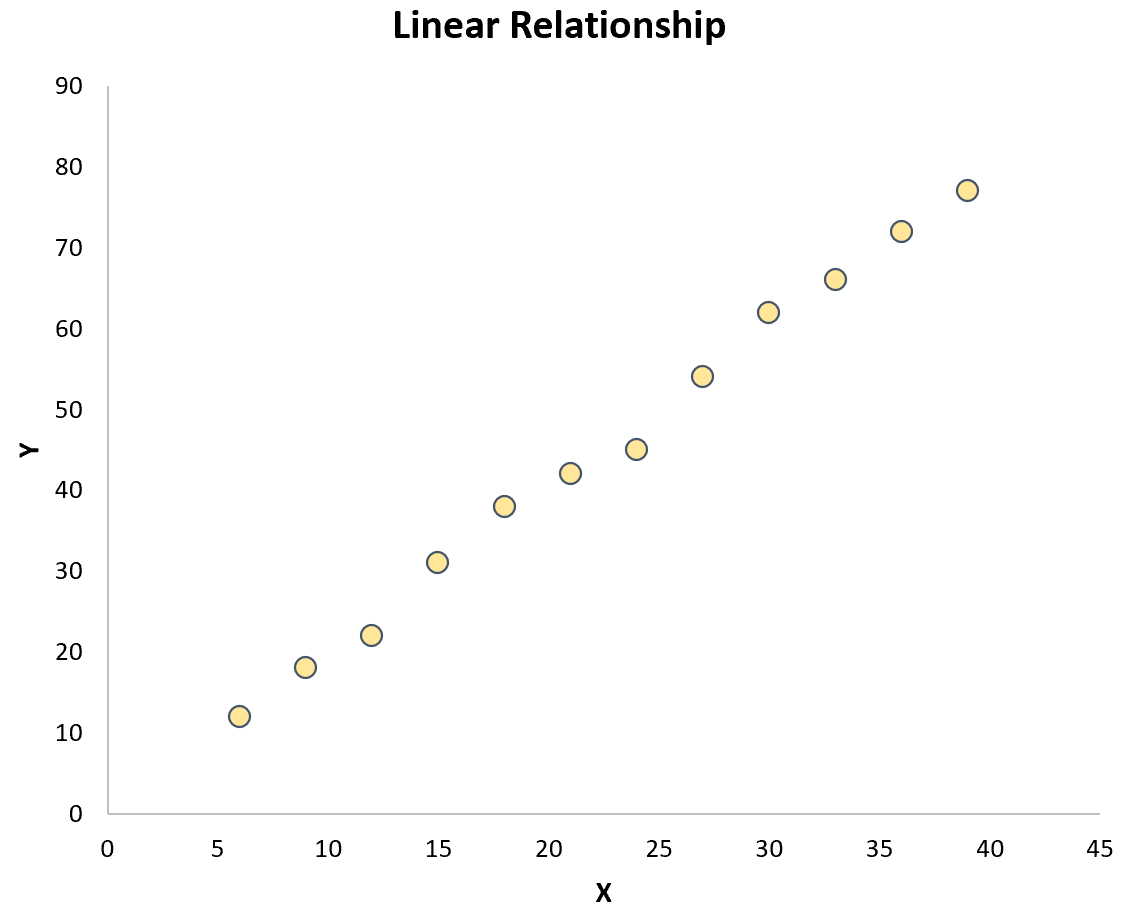
သို့သော်၊ အကယ်၍ အမှတ်များသည် ကွက်ကွက်တစ်ခွင်တွင် ကျပန်းကျပန်း ကွဲပြားသွားပါက သို့မဟုတ် အခြားသော ဆက်နွယ်မှု အမျိုးအစားအချို့ (ဥပမာ-လေးထောင့်ပုံ) ရှိပါက၊ ကိန်းရှင်များကြားတွင် linear ဆက်ဆံရေး မရှိပါ။

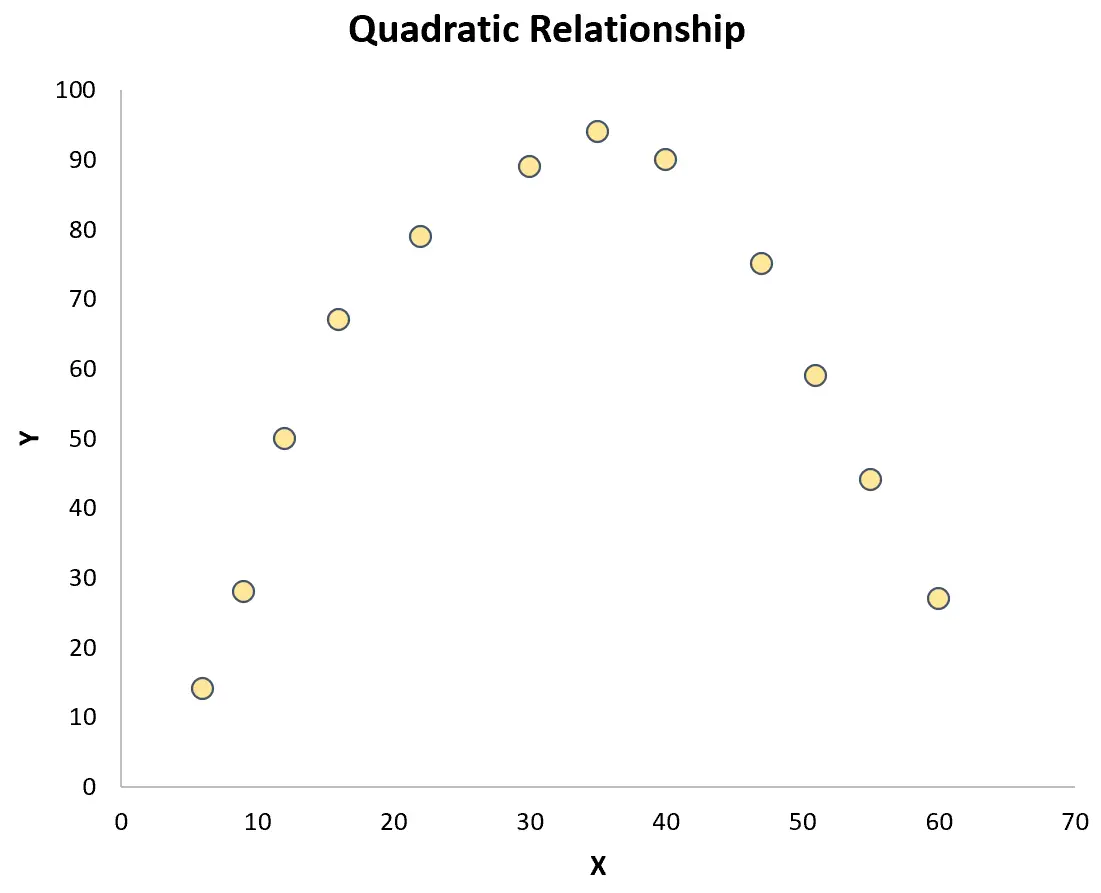
ဤကိစ္စတွင်၊ Pearson ဆက်စပ်ကိန်းဂဏန်းသည် ကိန်းရှင်များကြားရှိ ဆက်နွယ်မှုကို လုံလောက်စွာ ဖမ်းယူမည်မဟုတ်ပါ။

အယူအဆ 3- ပုံမှန်အခြေအနေ

Pearson correlation coefficient သည် ကိန်းရှင်နှစ်ခုအား ခန့်မှန်းခြေအားဖြင့် ပုံမှန်အတိုင်း ဖြန့်ဝေသည်ဟု လည်း ယူဆသည်။

ကိန်းရှင်တစ်ခုစီအတွက် histogram သို့မဟုတ် QQ ကွက်ကွက်ဖန်တီးခြင်းဖြင့် ဤယူဆချက်ကို အမြင်အာရုံဖြင့် အတည်ပြုနိုင်သည်။

1. Histogram

ဒေတာအစုတစ်ခု၏ ဟီစတိုဂရမ်သည် အကြမ်းဖျင်းအားဖြင့် ခေါင်းလောင်းပုံသဏ္ဌာန်ဖြစ်နေပါက၊ ဒေတာကို ပုံမှန်အားဖြင့် ဖြန့်ဝေနိုင်ဖွယ်ရှိသည်။

2. QQLand

“ quantile-quantile” ၏ အတိုကောက် QQ ကွက်ကွက်သည် x-axis တစ်လျှောက် သီအိုရီဆိုင်ရာ ကိန်းသေများကို ပြသသည့် ကွက်ကွက်အမျိုးအစားတစ်ခု (ဆိုလိုသည်မှာ သင့်ဒေတာသည် ပုံမှန်ဖြန့်ဝေမှုအတိုင်း ဖြစ်ပါက မည်သည့်နေရာတွင်ရှိမည်) နှင့် y-ဝင်ရိုးတစ်လျှောက် နမူနာအရေအတွက်များ။ (ဆိုလိုသည်မှာ သင့်ဒေတာ အမှန်တကယ် နေထိုင်သည့်နေရာ)။

ဒေတာတန်ဖိုးများသည် 45 ဒီဂရီထောင့်ဖြင့် ဖွဲ့စည်းထားသော အကြမ်းဖျင်းဖြောင့်မျဉ်းအတိုင်း လိုက်နာပါက ဒေတာကို ပုံမှန်အတိုင်း ဖြန့်ဝေသည်ဟု ယူဆပါသည်။

ကိန်းရှင်တစ်ခုအား ပုံမှန်ဖြန့်ဝေခြင်းရှိ၊

အကယ်၍ စမ်းသပ်မှု၏ p-value သည် အချို့သော အရေးပါမှုအဆင့် (ဥပမာ α = 0.05) အောက်တွင် ရှိနေပါက၊ ဒေတာကို ပုံမှန်အတိုင်း ဖြန့်ဝေခြင်း မဟုတ်ကြောင်း ပြောရန် သင့်တွင် လုံလောက်သော အထောက်အထားရှိသည်။

ပုံမှန်နှုန်းကို စမ်းသပ်ရန်အတွက် အသုံးများသော ကိန်းဂဏန်းစမ်းသပ်မှု သုံးခုရှိသည်။

1. Jarque-Bera စမ်းသပ်မှု

• Excel တွင် Jarque-Bera Test ကိုမည်သို့လုပ်ဆောင်ရမည်နည်း။
• R တွင် Jarque-Bera စမ်းသပ်မှုပြုလုပ်နည်း
• Python တွင် Jarque-Bera စမ်းသပ်မှုပြုလုပ်နည်း

2. Shapiro-Wilk စမ်းသပ်မှု

• R တွင် Shapiro-Wilk စမ်းသပ်မှုပြုလုပ်နည်း
• Python တွင် Shapiro-Wilk Test ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။

3. Kolmogorov-Smirnov စမ်းသပ်မှု

• R တွင် Kolmogorov-Smirnov စမ်းသပ်မှုပြုလုပ်နည်း
• Python တွင် Kolmogorov-Smirnov စမ်းသပ်မှုပြုလုပ်နည်း

Hypothesis 4- ဆက်စပ်အတွဲများ

Pearson ဆက်စပ်ကိန်းဂဏန်းတစ်ခုသည် ဒေတာအစုံရှိ စောင့်ကြည့်မှု တစ်ခုစီတွင် တန်ဖိုးတစ်စုံစီရှိရမည်ဟုလည်း ယူဆသည်။

ဤယူဆချက်သည် အတည်ပြုရန် လွယ်ကူသည်။ ဥပမာအားဖြင့်၊ သင်သည် ကိုယ်အလေးချိန်နှင့် အရပ်အကြား ဆက်စပ်မှုကို တွက်ချက်နေပါက၊ ဒေတာအတွဲရှိ ရှုမြင်မှုတစ်ခုစီတွင် အလေးချိန်အတွက် အတိုင်းအတာတစ်ခုနှင့် အမြင့်တိုင်းတာမှုရှိကြောင်း ရိုးရှင်းစွာစစ်ဆေးပါ။

Hypothesis 5- အစွန်းအထင်းမရှိပါ။

Pearson ဆက်စပ်ကိန်းဂဏန်းသည် ဒေတာအတွဲတွင် လွန်ကဲသောအစွန်းထွက်များမရှိဟုလည်း ယူဆသည်၊ အကြောင်းမှာ အစွန်းများသည် ဆက်နွယ်မှုကိန်းဂဏန်းတွက်ချက်မှုကို ပြင်းထန်စွာအကျိုးသက်ရောက်သောကြောင့်ဖြစ်သည်။

ယင်းကို သရုပ်ဖော်ရန်၊ အောက်ပါဒေတာအတွဲကို ထည့်သွင်းစဉ်းစားပါ။

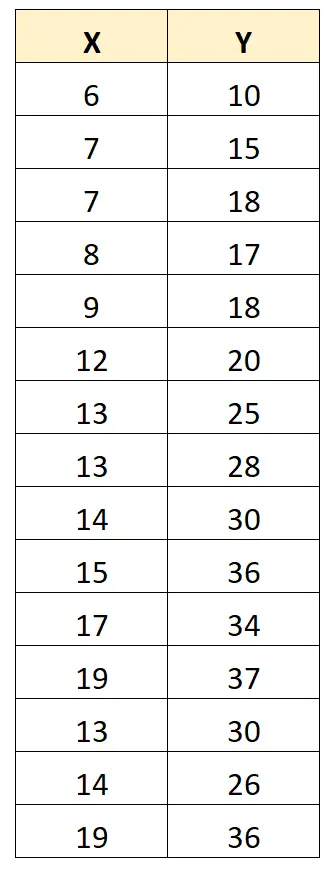
X နှင့် Y အကြားရှိ Pearson ဆက်စပ်ကိန်းသည် 0.949 ဖြစ်သည်။

သို့သော်၊ ကျွန်ုပ်တို့တွင် ဒေတာအတွဲတွင် အကြမ်းဖျင်းတစ်ခုရှိသည်ဆိုပါစို့။

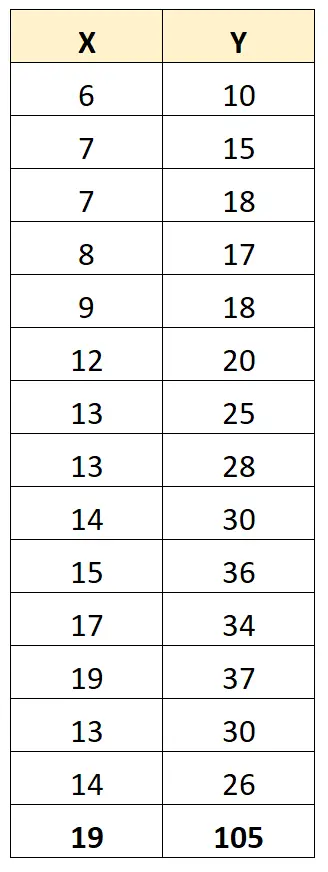
X နှင့် Y အကြားရှိ Pearson ဆက်စပ်ကိန်းသည် ယခုအခါ 0.711 ဖြစ်သည်။

ကိန်းရှင်နှစ်ခုကြားရှိ Pearson ဆက်စပ်ကိန်းကို သိသိသာသာ ပြောင်းလဲစေသည်။ ဤကိစ္စတွင်၊ ဒေတာအတွဲမှ အကြမ်းဖျင်းကို ဖယ်ရှားခြင်းသည် အဓိပ္ပာယ်ရှိပေမည်။

ဆက်စပ်- ပြီးပြည့်စုံသော လမ်းညွှန်- ဒေတာရှိ Outliers များကို မည်သည့်အချိန်တွင် ဖယ်ရှားမည်နည်း။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် Pearson ဆက်စပ်မှုဆိုင်ရာ နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

Pearson Correlation Coefficient ကို နိဒါန်း
APA ဖော်မတ်ဖြင့် Pearson ဆက်စပ်မှုကို မည်သို့အစီရင်ခံမည်နည်း။
Pearson Correlation Coefficient ကို ကိုယ်တိုင် တွက်ချက်နည်း