စာရင်းဇယားများတွင် ဖြစ်နိုင်ခြေအစုလိုက်အပြုံလိုက်လုပ်ဆောင်မှု (pmf) ဆိုသည်မှာ အဘယ်နည်း။

ဖြစ်နိုင်ခြေ အစုလိုက်အပြုံလိုက် လုပ်ဆောင်ချက် ၊ မကြာခဏ အတိုကောက် PMF သည် သီးခြားကျပန်းကိန်းရှင်သည် အချို့သော တန်ဖိုးတစ်ခုအပေါ် သက်ရောက်နိုင်ခြေကို ပြောပြသည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် သေတ္တာကို တစ်ကြိမ်လိပ်သည်ဆိုပါစို့။ အကယ်၍ ကျွန်ုပ်တို့သည် x တွင် ကိန်းဂဏာန်းများကို ဖော်ပြခွင့်ပြုပါက၊ x သည် မတူညီသောတန်ဖိုးများနှင့် တန်းတူဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း ဖော်ပြနိုင်သည်။

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

အန်စာတုံးများသည် 1 နှင့် 6 အကြား မည်သည့်နံပါတ်ပေါ်မဆို ဆင်းသက်ရန် တူညီသောအခွင့်အရေးရှိသည်။

ဤဖြစ်နိုင်ချေများကို ဖြစ်နိုင်ခြေအစုလိုက်အပြုံလိုက် လုပ်ဆောင်မှုအဖြစ် ကျွန်ုပ်တို့ မည်သို့ရေးသားနိုင်မည်နည်း။

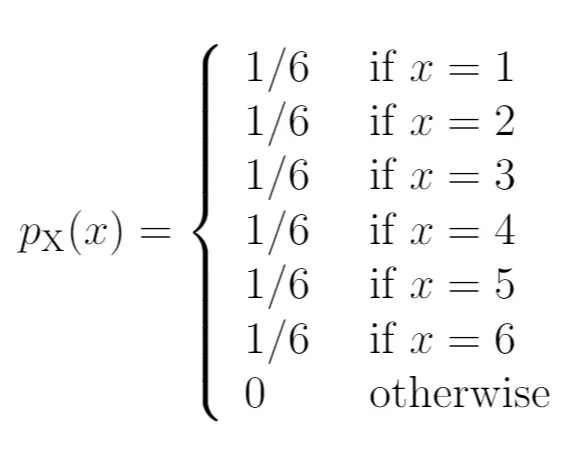
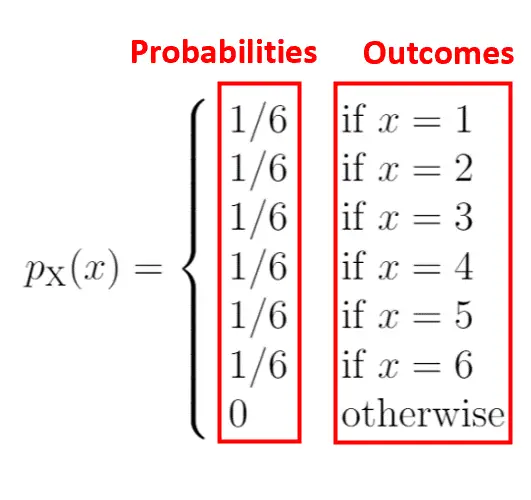
ပုံကြမ်း၏ ဘယ်ဘက်ခြမ်းသည် ညာဘက်ခြမ်းရှိ ရလဒ်များနှင့် ဆက်စပ်နိုင်ခြေကို ပြသည်-

ဖြစ်နိုင်ခြေအစုလိုက်အပြုံလိုက်လုပ်ဆောင်မှု၏ လက္ခဏာရပ်တစ်ခုမှာ ဖြစ်နိုင်ခြေအားလုံးကို 1 နှင့် ပေါင်းစည်းရမည်ဖြစ်သည်။

ဖြစ်နိုင်ခြေပေါင်းလဒ် = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1။

ဖြစ်နိုင်ခြေအစုလိုက်အပြုံလိုက်လုပ်ဆောင်မှုတစ်ခုအတွက် ပံ့ပိုးမှုသည် ခွဲခြမ်းစိတ်ဖြာသောကျပန်းကိန်းရှင်ယူနိုင်သည့်တန်ဖိုးများအစုကို ရည်ညွှန်းသည်။ ဤဥပမာတွင်၊ အသေခံတန်ဖိုးသည် ဤတန်ဖိုးများထဲမှ တစ်ခုခုကို ယူနိုင်သောကြောင့် ပံ့ပိုးမှုသည် {1၊ 2၊ 3၊ 4၊ 5၊ 6} ဖြစ်လိမ့်မည်။

ပံ့ပိုးမှုအပြင် PMF တန်ဖိုးသည် သုညဖြစ်သည်။ ဥပမာအားဖြင့်၊ ဤနံပါတ်များအနက်မှတစ်ခုမျှမပါဝင်သောကြောင့် “ 0” သို့မဟုတ် “ 7” သို့မဟုတ် “ 8” တွင်သေဆုံးခြင်းဖြစ်နိုင်ခြေသည် သုညဖြစ်သည်။

လက်တွေ့တွင်ဖြစ်နိုင်ခြေအစုလိုက်အပြုံလိုက်လုပ်ဆောင်ချက်များ

လက်တွေ့တွင်ဖြစ်နိုင်ခြေအစုလိုက်အပြုံလိုက်လုပ်ဆောင်မှုများ၏အသုံးအများဆုံးနမူနာနှစ်ခုသည် binomial ဖြန့်ဖြူးမှု နှင့် Poisson ဖြန့်ဖြူးမှုနှင့် ပတ်သက်သည်။

Binomial ဖြန့်ဖြူးခြင်း။

ကျပန်း variable X သည် binomial distribution ကို လိုက်နာပါက၊ X = k အောင်မြင်မှု ဖြစ်နိုင်ခြေကို အောက်ပါဖော်မြူလာဖြင့် ရှာတွေ့နိုင်သည်-

P(X=k) = _n C _k * p ^k * (1-p) ^nk

ရွှေ-

• n: စမ်းသပ်မှုအရေအတွက်
• k: အောင်မြင်မှုအရေအတွက်
• p- ပေးထားသော စမ်းသပ်မှုတစ်ခုတွင် အောင်မြင်နိုင်ခြေ
• _n C _k : n စမ်းသပ်မှုများတွင် k အောင်မြင်မှုများရရှိရန် နည်းလမ်းများ

ဥပမာ၊ အကြွေစေ့ကို ၃ ကြိမ်လှန်တယ်ဆိုပါစို့။ ဤ 3 ကြိမ်တွင် 0၊ 1၊ 2 နှင့် 3 ခေါင်းများကို ရယူရန် ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန် အထက်ဖော်ပြပါ ဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။

• P(X=0) = ₃ C ₀ * 0.5 ⁰ * (1-0.5) ^3-0 = 1 * 1 * (0.5) ³ = 0.125၊
• P(X=1) = ₃ C ₁ * 0.5 ¹ * (1-0.5) ^3-1 = 1 * 1 * (0.5) ² = 0.375၊
• P(X=2) = ₃ C ₂ * 0.5 ² * (1-0.5) ^3-2 = 1 * 1 * (0.5) ¹ = 0.375၊
• P(X=3) = ₃ C ₃ * 0.5 ³ * (1-0.5) ^3-3 = 1 * 1 * (0.5) ⁰ = 0.125၊

ငါးဖြန့်ဖြူးရေး

ကျပန်းပြောင်းလဲနိုင်သော X သည် Poisson ဖြန့်ဝေမှုကို လိုက်နာပါက၊ ထို့နောက် X = k အောင်မြင်မှုဖြစ်နိုင်ခြေကို အောက်ပါဖော်မြူလာဖြင့် ရှာတွေ့နိုင်သည်-

P(X=k) = λ ^k * e ^{– λ} / k!

ရွှေ-

• λ: တိကျသောကြားကာလတစ်ခုအတွင်း ဖြစ်ပေါ်သည့် ပျမ်းမျှအောင်မြင်မှုအရေအတွက်
• k: အောင်မြင်မှုအရေအတွက်
• e- ခန့်မှန်းခြေအားဖြင့် 2.71828 နှင့်ညီမျှသော ကိန်းသေတစ်ခု

ဥပမာအားဖြင့်၊ ဆေးရုံတစ်ခုသည် တစ်နာရီလျှင် ပျမ်းမျှ မွေးဖွားမှု ၂ ခု ခံစားရသည်ဆိုပါစို့။ 0၊ 1၊ 2၊ 3 မွေးဖွားမှု စသည်ဖြင့် တွေ့ကြုံရနိုင်ခြေကို ဆုံးဖြတ်ရန် အထက်ဖော်ပြပါ ဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။ သတ်မှတ်နာရီအတွင်း

• P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0.1353
• P(X=1) = 2 ¹ * e ^{– 2/1} ! = 0.2707
• P(X=2) = 2 ² * e ^{– 2/2} ! = 0.2707
• P(X=3) = 2 ³ * e ^{– 2/3} ! = 0.1805

PMF ကိုကြည့်ပါ။

ဘားဂရပ်များဖြင့် ကျွန်ုပ်တို့သည် ဖြစ်နိုင်ခြေအစုလိုက်အပြုံလိုက် လုပ်ဆောင်ချက်များကို မြင်ယောင်လေ့ရှိသည်။

ဥပမာအားဖြင့်၊ အောက်ဖော်ပြပါဘားဇယားသည် ယခင်ဥပမာတွင်ဖော်ပြထားသော Poisson ဖြန့်ဖြူးမှုအတွက် တစ်နာရီလျှင်မွေးဖွားမှုအရေအတွက်နှင့်ဆက်စပ်နိုင်ခြေများကိုပြသသည်-

မွေးဖွားမှုအရေအတွက်သည် အဆုံးမရှိအထိ တိုးသွားနိုင်သည်ကို သတိပြုပါ သို့သော် ဖြစ်နိုင်ခြေများသည် 10 နောက်ပိုင်းတွင် အလွန်နည်းပါးသွားသည့်အတွက် ၎င်းတို့ကို ဘားဂရပ်ပေါ်တွင်ပင် မမြင်နိုင်ပေ။

PMF ၏ ဂုဏ်သတ္တိများ

ဖြစ်နိုင်ခြေအစုလိုက်အပြုံလိုက်လုပ်ဆောင်ချက်တွင် အောက်ပါဂုဏ်သတ္တိများရှိသည်။

1. ဖြစ်နိုင်ခြေအားလုံးသည် အပြုသဘောဆောင်သော ထောက်ခံမှုဖြစ်သည်။ ဥပမာအားဖြင့်၊ 1 နှင့် 6 အကြားကျသောသေဆုံးခြင်း၏ဖြစ်နိုင်ခြေသည် အပြုသဘောဖြစ်ပြီး အခြားရလဒ်များအားလုံး၏ဖြစ်နိုင်ခြေမှာ သုညဖြစ်သည်။

2. ရလဒ်များအားလုံးတွင် 0 နှင့် 1 အကြားဖြစ်နိုင်ခြေရှိသည်။ ဥပမာအားဖြင့်၊ 1 နှင့် 6 အကြားတွင် သေဆုံးမှုဖြစ်နိုင်ခြေသည် 1/6 သို့မဟုတ် 0.1666666 ရလဒ်တစ်ခုစီအတွက်ဖြစ်သည်။

3. ဖြစ်နိုင်ခြေအားလုံး၏ ပေါင်းလဒ်သည် 1 နှင့် ညီမျှရပါမည်။ ဥပမာ၊ အချို့သောကိန်းတစ်ခုပေါ်တွင် ကျလာသော ဖြစ်နိုင်ခြေများ ပေါင်းလဒ်သည် 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1 ဖြစ်သည်။ /၆=၁။

ထပ်လောင်းအရင်းအမြစ်များ

Random variable တွေက ဘာတွေလဲ။
CDF သို့မဟုတ် PDF- ကွာခြားချက်ကား အဘယ်နည်း။
binomial ဖြန့်ဖြူးခြင်းအတွက် နိဒါန်းတစ်ခု
Poisson ဖြန့်ဖြူးမှုမိတ်ဆက်