Polynomial ဆုတ်ယုတ်မှု

အားဖြင့် Benjamin Anderson ဩဂုတ် 2, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ကိန်းဂဏန်းများဆိုင်ရာ ကိန်းဂဏန်းများ ဆုတ်ယုတ်မှုဟူသည် မည်ကဲ့သို့ လုပ်ဆောင်ကြောင်းကို ရှင်းပြထားသည်။ ထို့အပြင်၊ polynomial regression လုပ်ဆောင်သည့် ဥပမာတစ်ခုကို သင်တွေ့မြင်နိုင်မည်ဖြစ်ပါသည်။

polynomial regression ဆိုတာ ဘာလဲ။

Polynomial regression သို့မဟုတ် polynomial regression သည် အမှီအခိုကင်းသော variable X နှင့် dependent variable Y အကြား ဆက်နွယ်မှုကို polynomial ကို အသုံးပြု၍ စံနမူနာပြုသည့် ဆုတ်ယုတ်မှုပုံစံတစ်ခုဖြစ်သည်။

ဥပမာအားဖြင့်၊ လေးထောင့်ကိန်းဂဏန်း ဆုတ်ယုတ်မှုပုံစံအတွက် ညီမျှခြင်းမှာ y=β ₀ +β ₁ x+β ₂ x ² +ε ဖြစ်သည်။

Polynomial regression သည် ကိန်းဂရပ်များဖြစ်သည့် polynomial မျဉ်းကွေးများဖြစ်သည့် ဒေတာအတွဲများနှင့် ကိုက်ညီရန်အတွက် အသုံးဝင်သည်။ ထို့ကြောင့်၊ ဒေတာနမူနာတစ်ခု၏ အစက်ကွက်ကွက်တွင် parabola ပုံသဏ္ဍာန်ရှိနေပါက၊ linear regression model ထက် quadratic regression model ကို တည်ဆောက်ခြင်းသည် ပိုကောင်းပါလိမ့်မည်။ ဤနည်းအားဖြင့်၊ regression model equation သည် data sample နှင့် ပိုအဆင်ပြေလိမ့်မည်။

polynomial regression သည် exponential regression နှင့် logarithmic regression တို့ကဲ့သို့ linear nonlinear regression အမျိုးအစားတစ်ခုဖြစ်ကြောင်း သတိပြုပါ။

Polynomial Regression ဖော်မြူလာ

ကိန်းဂဏန်း ဆုတ်ယုတ်မှုပုံစံအတွက် ညီမျှခြင်းမှာ y=β ₀ +β ₁ x+β ₂ x ² +β ₃ x ³ …+β _m x ^m +ε ဖြစ်သည်။

$y=\beta_0+\beta_1 x+\beta_2 x^2+\beta_3 x^3+\dots+\beta_m x^m+\varepsilon$

ရွှေ-

$y$

dependent variable ဖြစ်ပါတယ်။
$x$

လွတ်လပ်သောကိန်းရှင်ဖြစ်သည်။
$\beta_0$

polynomial regression equation ၏ ကိန်းသေဖြစ်ပါသည်။
$\beta_i$

ကိန်းရှင်နှင့်ဆက်စပ်နေသော ဆုတ်ယုတ်မှုကိန်းဂဏန်းဖြစ်သည်။

$x^i$

.
$\bm{\varepsilon}$

၎င်းသည် အမှားအယွင်း သို့မဟုတ် ကျန်ရှိနေသော၊ ဆိုလိုသည်မှာ သတိပြုမိသောတန်ဖိုးနှင့် မော်ဒယ်မှ ခန့်မှန်းတန်ဖိုးကြား ကွာခြားချက်ကို ဆိုလိုသည်။

ဒီတော့ စုစုပေါင်းနမူနာတစ်ခုရရင်

$n$

လေ့လာချက်များအရ၊ ကျွန်ုပ်တို့သည် မက်ထရစ်ပုံစံဖြင့် polynomial regression model ကို အဆိုပြုနိုင်သည်-

$\begin{pmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{pmatrix}=\begin{pmatrix}1&x_1&x_1^2&\dots&x_1^m\\1&x_2&x_2^2&\dots&x_2^m\\1&x_3&x_3^2&\dots&x_3^m\\ \vdots&\vdots&\ddots&\vdots\\1&x_{n}&x_n^2&\dots&x_n^m\end{pmatrix}\cdot\begin{pmatrix}\beta_0\\\beta_1\\\beta_2\\\vdots\\\beta_m\end{pmatrix}+\begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\vdots\\\varepsilon_n\end{pmatrix}$

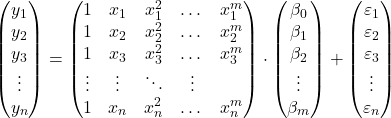
အထက်ဖော်ပြပါ မက်ထရစ်အသုံးအနှုန်းကို မက်ထရစ်တစ်ခုစီသို့ စာလုံးတစ်လုံးစီ သတ်မှတ်ခြင်းဖြင့် ပြန်လည်ရေးသားနိုင်သည်-

$Y=X\beta+\varepsilon$

ထို့ကြောင့်၊ အနည်းဆုံး စတုရန်းစံသတ်မှတ်ချက်ကို ကျင့်သုံးခြင်းဖြင့်၊ ပေါလီnomial ဆုတ်ယုတ်မှုပုံစံ၏ ဖော်မြူလာကို ခန့်မှန်းခြင်းအတွက် ဖော်မြူလာ သို့ ရောက်ရှိနိုင်သည်-

$\widehat{\beta}=\left(X^tX\right)^{-1}X^tY$

သို့သော်၊ ဤတွက်ချက်မှုများကို လက်ဖြင့်ပြုလုပ်ခြင်းသည် အလွန်ပင်ပန်းပြီး အချိန်ကုန်သောကြောင့်၊ သင်သည် polynomial regression model ကိုပိုမိုမြန်ဆန်စွာလုပ်ဆောင်နိုင်စေသည့်ကွန်ပြူတာဆော့ဖ်ဝဲ (Minitab သို့မဟုတ် Excel ကဲ့သို့) အသုံးပြုရန် ပို၍အဆင်ပြေပါသည်။

polynomial regression model ၏ ဥပမာ

ယခု ကျွန်ုပ်တို့သည် များစွာသော ဆုတ်ယုတ်ခြင်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်းကို မည်သို့လုပ်ဆောင်ကြောင်းကို သိရှိပြီး သဘောတရားကို အပြည့်အဝနားလည်ရန် လက်တွေ့ဘဝဥပမာကို ကြည့်ကြပါစို့။

ပထမဦးစွာ၊ ဒေတာဂရပ်တွင် ပေါလီအမည်မျဉ်းကွေးပုံသဏ္ဍာန်ရှိသောအခါတွင် ကိန်းဂဏန်းများ ဆုတ်ယုတ်မှုပုံစံကို လုပ်ဆောင်သင့်သည်ဟု မှတ်သားထားသင့်သည်။ ဥပမာအားဖြင့်၊ dotplot သည် ကုဗမျဉ်းပုံစံဖြစ်ပြီး၊ ကျွန်ုပ်တို့သည် တတိယဒီဂရီ polynomial regression ပုံစံကို တည်ဆောက်ရန် လိုအပ်သည်။

ထို့ကြောင့် အောက်ပါပုံတွင် သင်မြင်ရသည့်အတိုင်း၊ ကျွန်ုပ်တို့၏ဒေတာ၏ အစက်ချကွက်သည် လေးထောင့်ပုံသဏ္ဍာန်ရှိပြီး၊ အမှီအခိုကင်းသော variable ၏တန်ဖိုးကို ကျွန်ုပ်တို့တိုးလာသည်နှင့်အမျှ မှီခိုသောကိန်းရှင်သည် ပိုမိုလျင်မြန်စွာကြီးထွားလာသောကြောင့်ဖြစ်သည်။ ဤကိစ္စတွင်၊ linear regression model ကိုလုပ်ဆောင်ခဲ့ပြီး၊ သင်တွေ့မြင်ရသည့်အတိုင်း ၎င်းသည် အမှတ်များအားလုံးနှင့် မျဉ်း၏အထက်တွင်ရှိသော အပိုင်းများနှင့် မျဉ်းအောက်ရှိ အပိုင်းများပါရှိသောကြောင့် ၎င်းတွင် အမှတ်များ ကောင်းစွာမကိုက်ညီပါ။

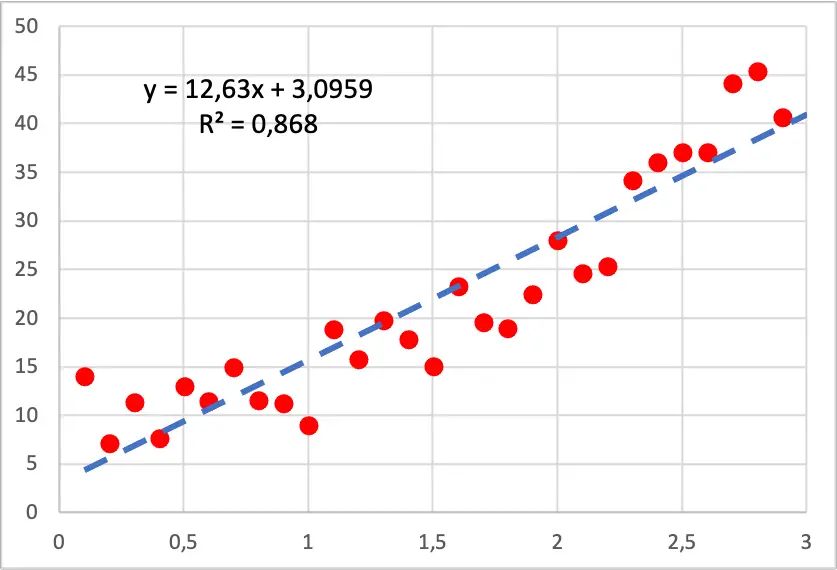
အခြားတစ်ဖက်တွင်၊ ကျွန်ုပ်တို့သည် လေးထောင့်ကိန်းဂဏန်းများ ဆုတ်ယုတ်မှုပုံစံကို လုပ်ဆောင်ပါက၊ ၎င်းသည် အောက်ဖော်ပြပါပုံတွင်မြင်ရသည့်အတိုင်း နမူနာဒေတာနှင့် ပိုမိုကိုက်ညီပါသည်။

ထို့အပြင်၊ polynomial regression model ကို တီထွင်သောအခါ၊ ဆုံးဖြတ်ခြင်း၏ coefficient သည် 86.80% မှ 94.05% သို့ သိသိသာသာ တိုးတက်လာသည်။ ထို့ကြောင့်၊ ဆုတ်ယုတ်မှုပုံစံအသစ်သည် ဒေတာအတွဲကို များစွာပိုကောင်းအောင် ရှင်းပြသည်။

အခြားတစ်ဖက်တွင်၊ ကျွန်ုပ်တို့သည် polynomial regression ကိုလုပ်ဆောင်ရန် လိုအပ်သည့်နောက်ထပ်အချက်တစ်ချက်မှာ အကြွင်းအကျန်များကို ပုံဖော်ခြင်းပင်ဖြစ်သည်။ မျဉ်းကြောင်း ဆုတ်ယုတ်မှုတစ်ခုတွင် ကျန်ရှိသောဂရပ်သည် parabola ပုံသဏ္ဍာန် သို့မဟုတ် အခြားပိုလီအမည်တစ်မျိုး၏ ပုံသဏ္ဍာန်ရှိပါက၊ ကိန်းဂဏန်းများ ဆုတ်ယုတ်မှုပုံစံသည် လေ့လာထားသော အချက်အလက်နှင့် ပိုကိုက်ညီမည်မှာ သေချာပါသည်။

အခြားလိုင်းမဟုတ်သော ဆုတ်ယုတ်မှုအမျိုးအစားများ

အဓိကအားဖြင့် nonlinear regression အမျိုးအစားသုံးမျိုးရှိသည်။

Polynomial Regression – ဆုတ်ယုတ်မှုပုံစံ ညီမျှခြင်းသည် ပေါင်းကိန်းတစ်ခု၏ ပုံစံဖြစ်သည်။
လော့ဂရစ်သမ်ဆုတ်ယုတ်မှု – လွတ်လပ်သောကိန်းရှင်၏ လော့ဂရစ်သမ်ကို ယူသည်။
Exponential Regression : အမှီအခိုကင်းသော ကိန်းရှင်ကို ညီမျှခြင်း၏ ထပ်ကိန်းတွင် တွေ့နိုင်သည်။

➤ လော့ဂရစ်သမ် ဆုတ်ယုတ်မှုကို ကြည့်ပါ။
➤- Exponential Regression ကိုကြည့်ပါ။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။