Google sheets ရှိ polynomial regression (တစ်ဆင့်ပြီးတစ်ဆင့်)

ဆုတ်ယုတ်မှု ခွဲခြမ်းစိတ်ဖြာခြင်းကို တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် တုံ့ပြန်မှုကိန်းရှင် တစ်ခုကြား ဆက်စပ်မှုကို အရေအတွက်သတ်မှတ်ရန်အတွက် အသုံးပြုသည်။

ဆုတ်ယုတ်မှုခွဲခြမ်းစိတ်ဖြာမှု၏ အသုံးအများဆုံးအမျိုးအစားမှာ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှု ဖြစ်ပြီး၊ ခန့်မှန်းသူကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်သည် မျဉ်းကြောင်းဆက်စပ်မှုရှိသည့်အခါ အသုံးပြုသည်။

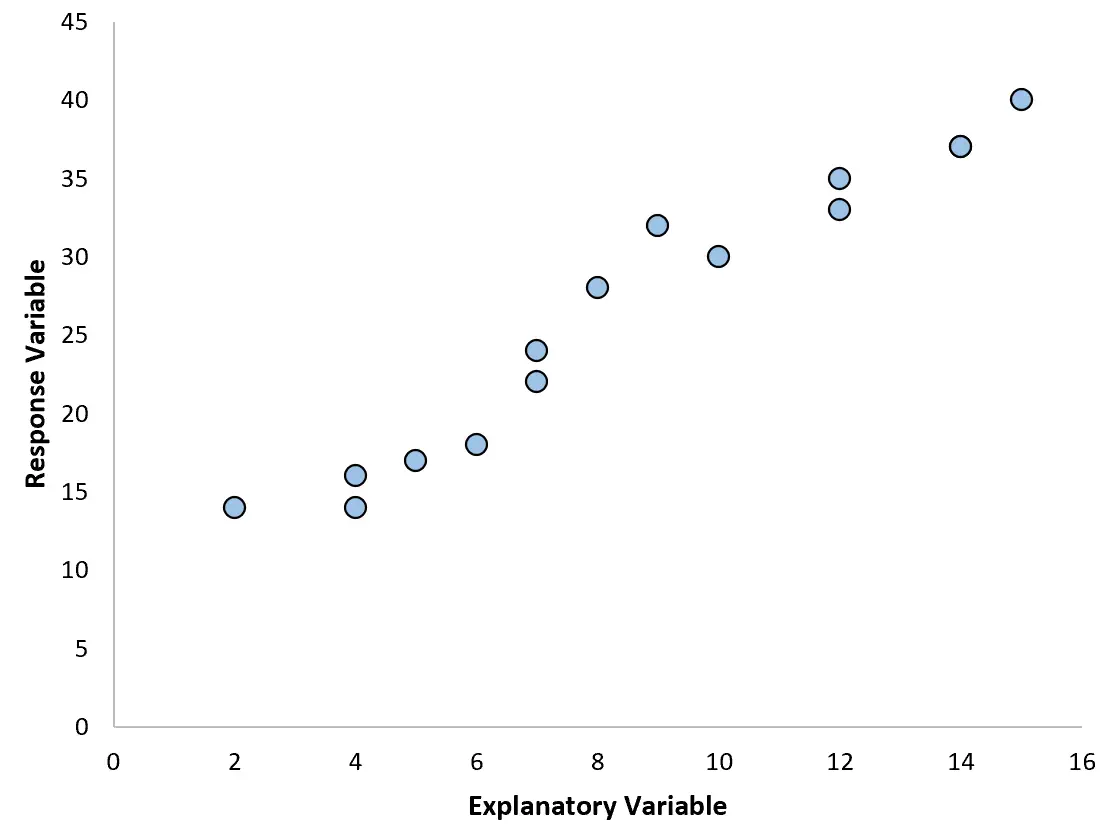
သို့သော် တစ်ခါတစ်ရံတွင် ကြိုတင်ခန့်မှန်းကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်ကြား ဆက်ဆံရေးသည် လိုင်းမဟုတ်ပေ။

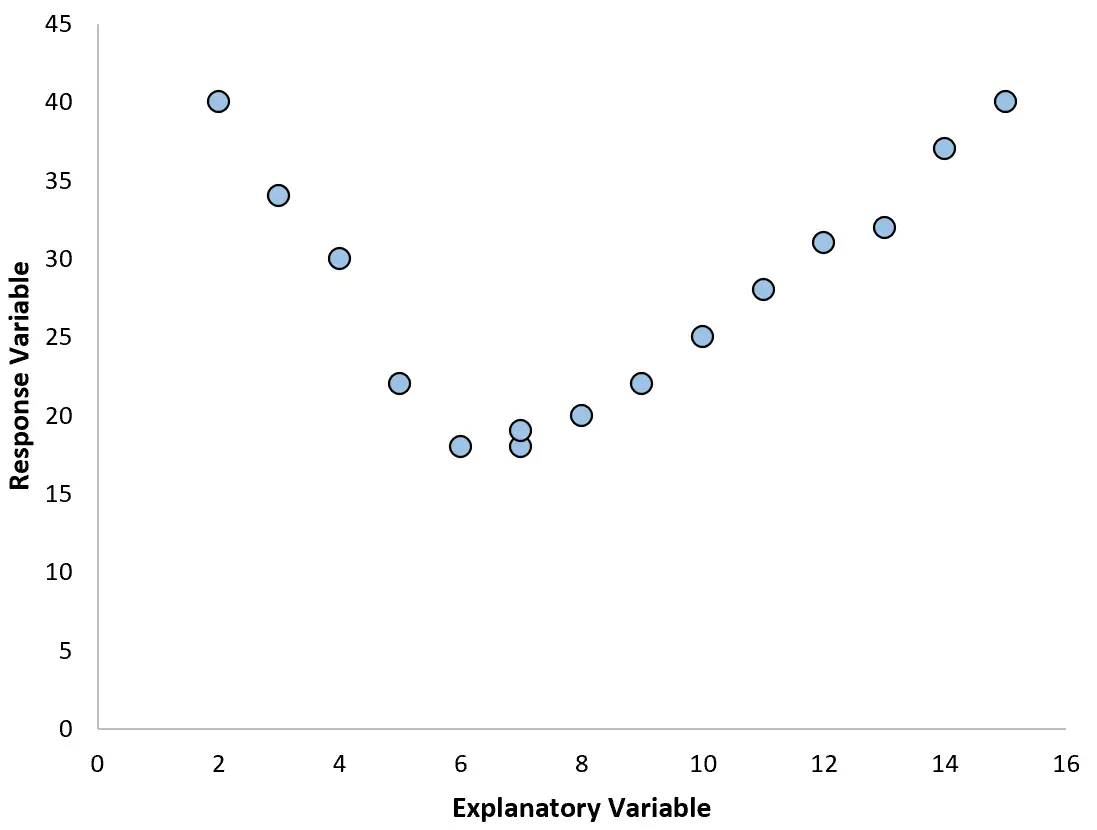
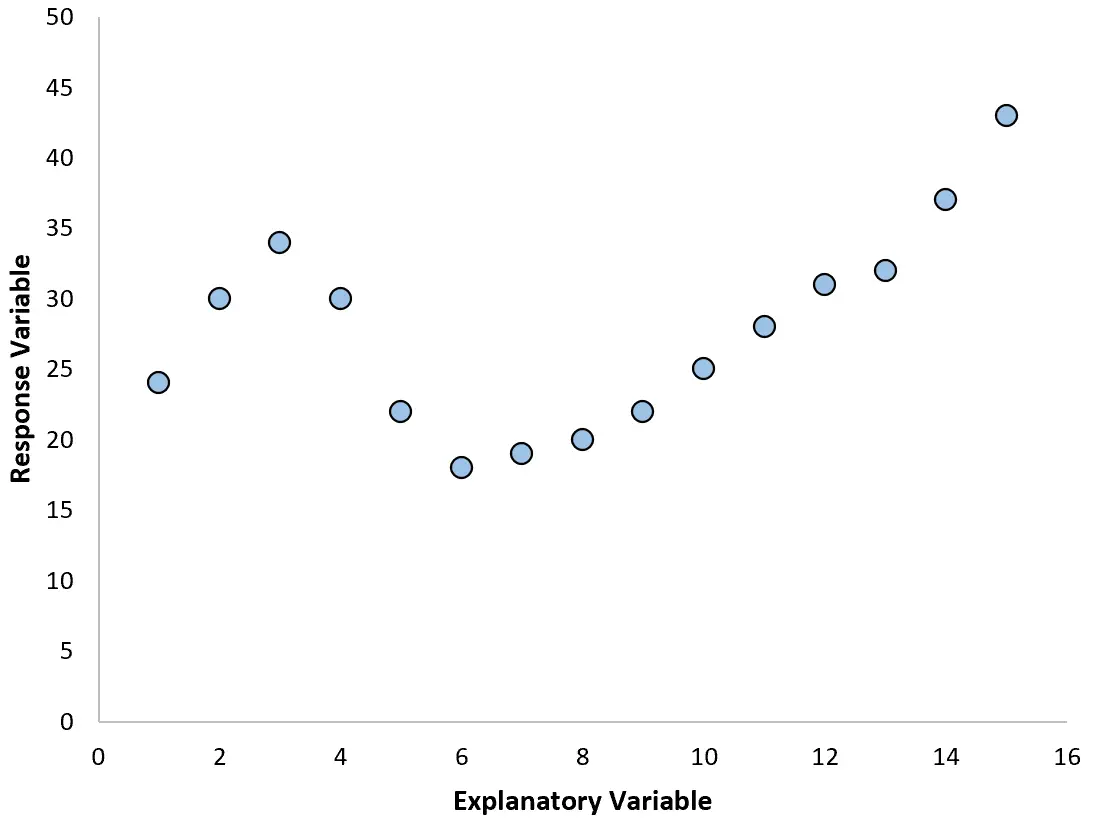
ဤကိစ္စများတွင်၊ ကိန်းရှင်များကြားတွင် linear မဟုတ်သော ဆက်နွယ်မှုကို တွက်ချက်နိုင်သည့် polynomial regression ကို အသုံးပြုခြင်းသည် အဓိပ္ပါယ်ရှိစေသည်။

ဤသင်ခန်းစာသည် Google Sheets တွင် polynomial regression လုပ်ဆောင်ပုံအဆင့်ဆင့်ကို ဥပမာပေးပါသည်။

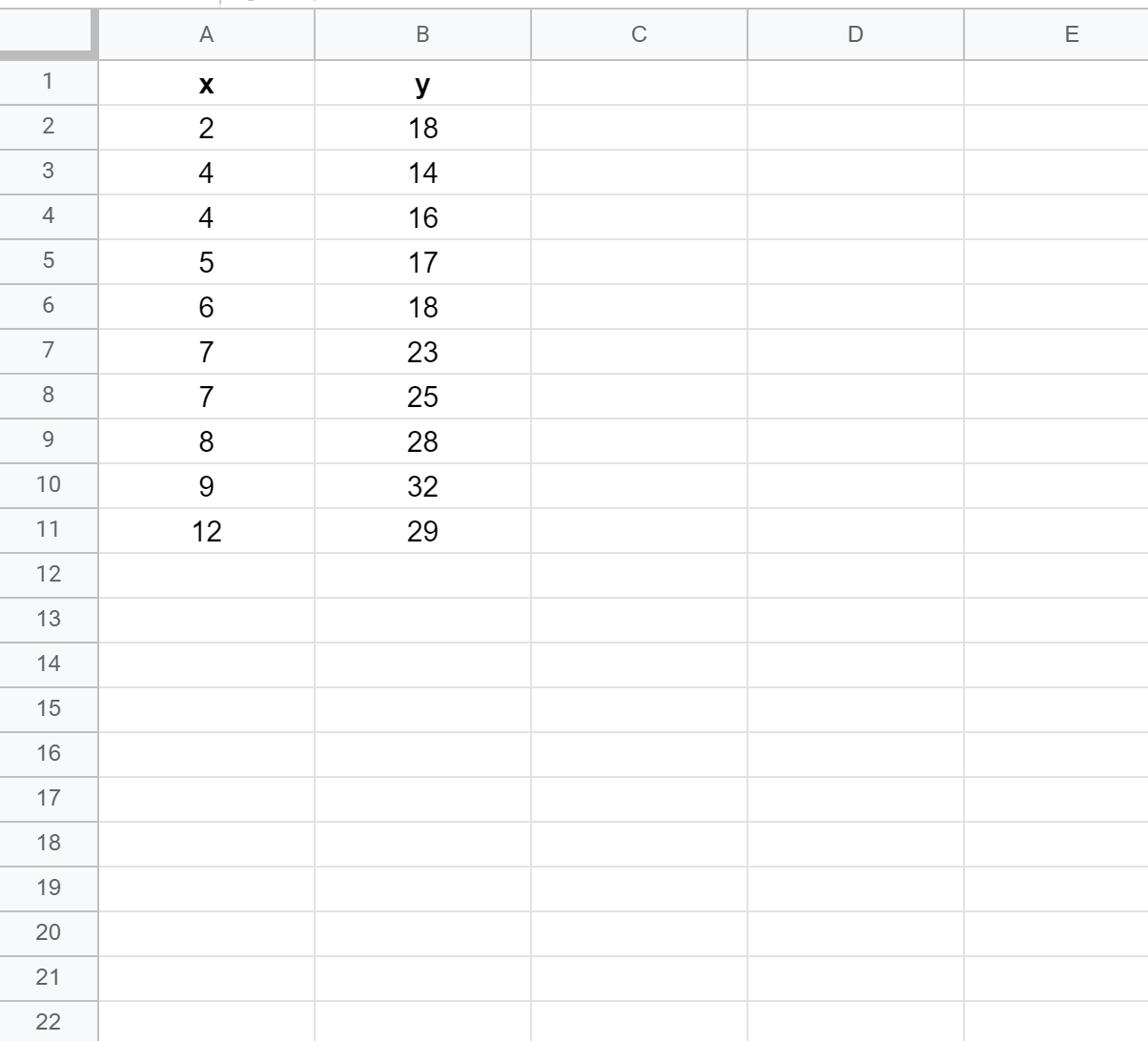
အဆင့် 1: ဒေတာကိုဖန်တီးပါ။

ဦးစွာ၊ အောက်ပါတန်ဖိုးများဖြင့် ဒေတာအတွဲအတုတစ်ခုကို ဖန်တီးကြပါစို့။

အဆင့် 2- အပိုင်းအစတစ်ခုကို ဖန်တီးပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် ဒေတာကိုမြင်ယောင်နိုင်ရန် အပိုင်းအစတစ်ခုကို ဖန်တီးပါမည်။

ပထမဦးစွာ အောက်ပါအတိုင်း ဆဲလ် A2:B11 ကို မီးမောင်းထိုးပြပါ ။

ထို့နောက် Insert tab ကိုနှိပ်ပါ၊ ထို့နောက် drop-down menu မှ Chart ကို နှိပ်ပါ။

မူရင်းအားဖြင့်၊ Google Sheets သည် အပိုင်းအစတစ်ခုကို ထည့်သွင်းပါမည်-

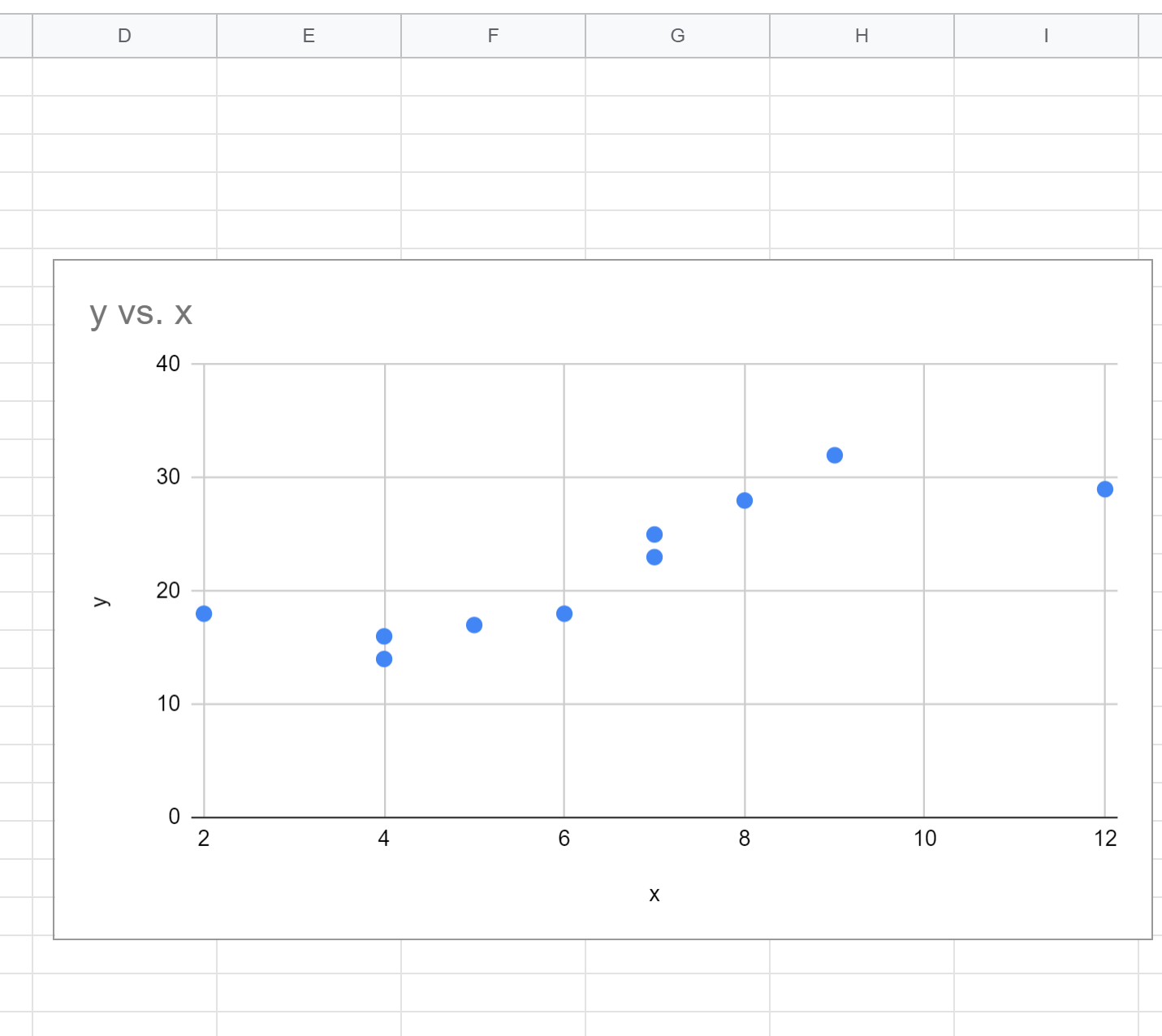
အဆင့် 3- Polynomial Regression Equation ကိုရှာပါ။

ထို့နောက်၊ ညာဘက်ရှိ ဂရပ်ဖစ်အယ်ဒီတာ ဝင်းဒိုးကိုပြသရန် scatterplot ပေါ်ရှိ မည်သည့်နေရာကိုမဆို နှစ်ချက်နှိပ်ပါ။

ထို့နောက် စီးရီးကို နှိပ်ပါ ။ ထို့နောက် အောက်သို့ဆင်းပြီး Trendline ဘေးရှိ အကွက်ကို အမှန်ခြစ်ပြီး Type ကို Polynomial သို့ ပြောင်းပါ။ အညွှန်းအတွက်၊ Use Equation ကို ရွေးပါ၊ ထို့နောက် Show ^R2 ဘေးရှိ အကွက်ကို အမှန်ခြစ်ပါ။

၎င်းသည် အောက်ပါပုံသေနည်းကို scatterplot ၏အထက်တွင် ပေါ်လာစေလိမ့်မည်-

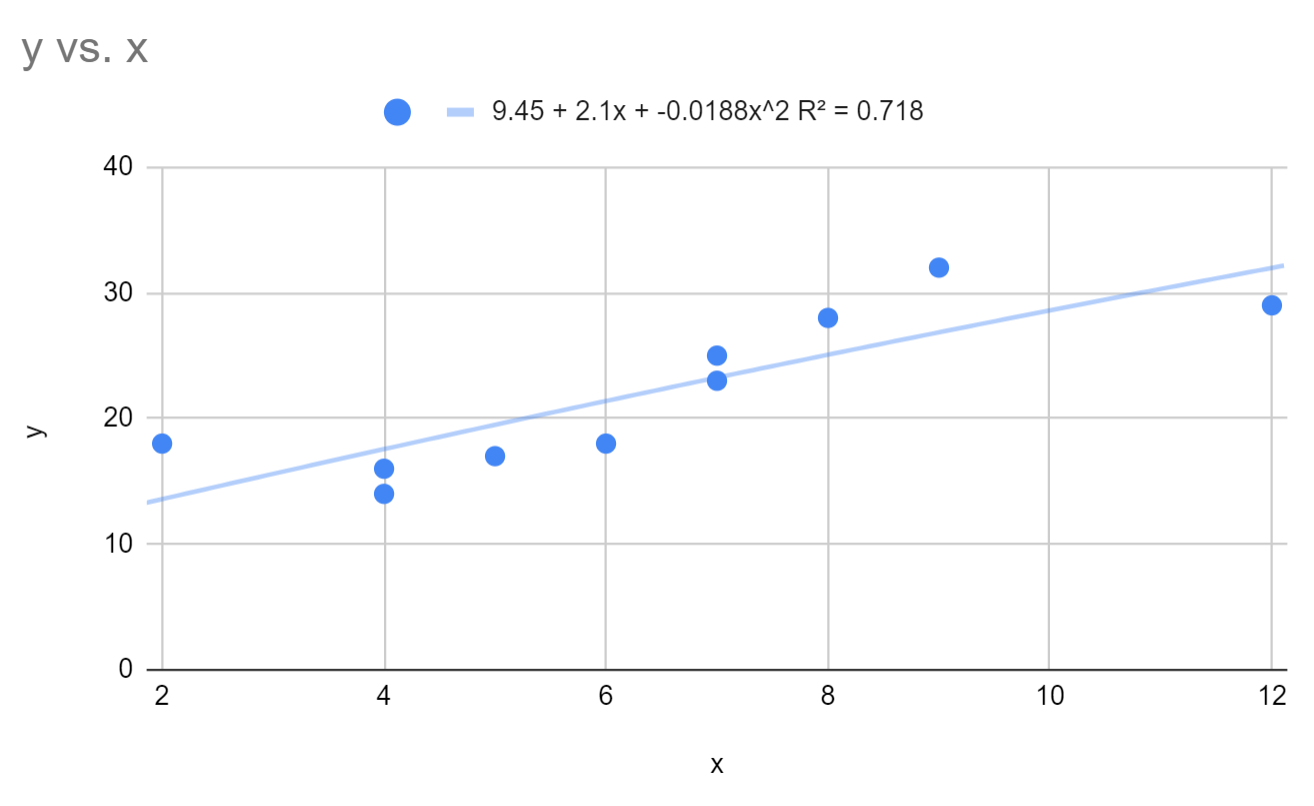
တပ်ဆင်ထားသော polynomial regression equation သည်-

y = 9.45 + 2.1x – 0.0188x ^၂

ဤမော်ဒယ်အတွက် R-squared သည် 0.718 ဖြစ်သည်။

R နှစ်ထပ်ကိန်း သည် ခန့်မှန်းသူကိန်းရှင်များဖြင့် ရှင်းပြနိုင်သည့် တုံ့ပြန်မှုကိန်းရှင်တွင် ကွဲလွဲမှုရာခိုင်နှုန်းကို ပြောပြသည်ကို သတိရပါ။ တန်ဖိုးမြင့်လေ မော်ဒယ်က ပိုကောင်းလေပါပဲ။

ထို့နောက်၊ ဂရပ်တည်းဖြတ်မှုတွင် polynomial ၏ဒီဂရီကို 3 သို့ပြောင်းပါ-

၎င်းသည် အောက်ပါပုံသေနည်းကို scatterplot ၏အထက်တွင် ပေါ်လာစေလိမ့်မည်-

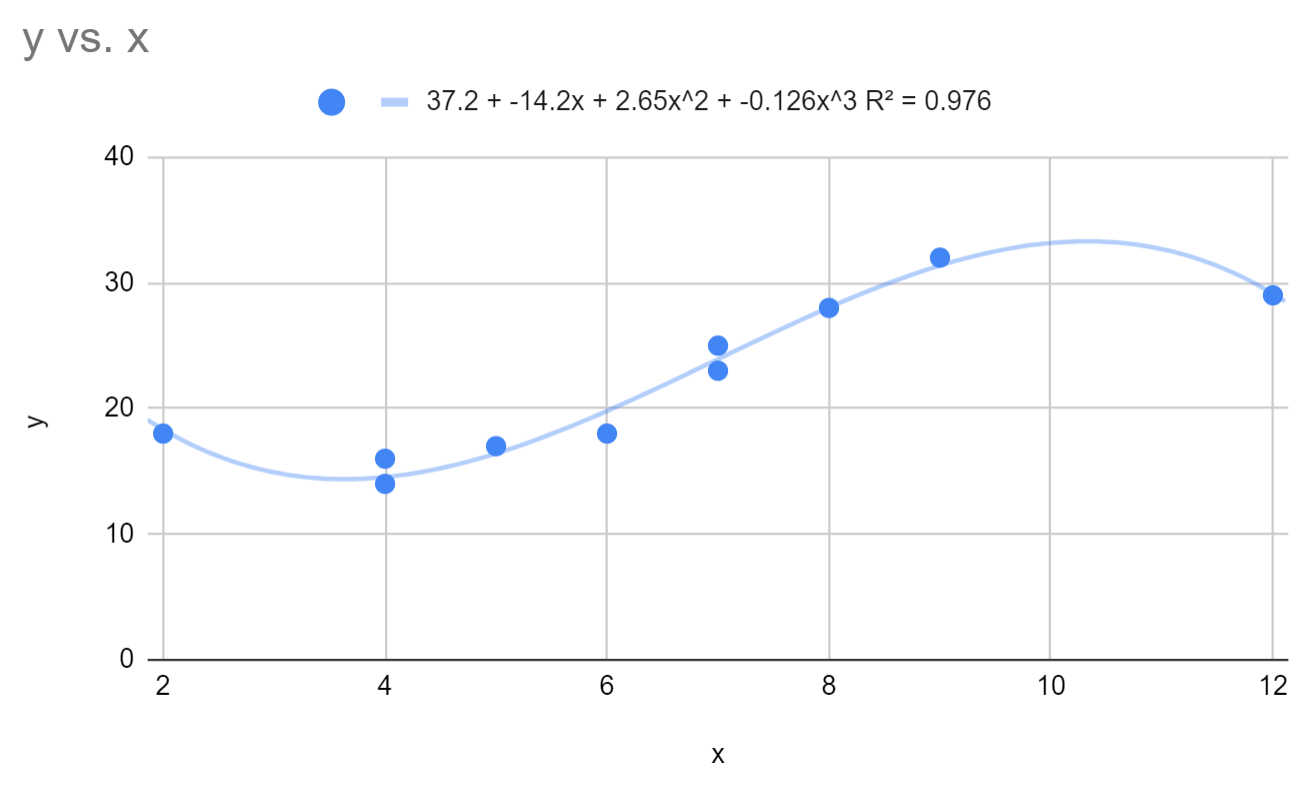
၎င်းသည် တပ်ဆင်ထားသော polynomial regression equation ကို ပြောင်းလဲသည်-

y = 37.2 – 14.2x + 2.64x ² – 0.126x ³

ဤမော်ဒယ်အတွက် R-squared သည် 0.976 ဖြစ်သည်။

ဤမော်ဒယ်၏ R-squared သည် ဒီဂရီ 2 ရှိသော polynomial regression model ထက် သိသိသာသာ မြင့်မားသည်ကို သတိပြုပါ။ ၎င်းသည် ဤဆုတ်ယုတ်မှုပုံစံသည် အရင်းခံဒေတာ၏လမ်းကြောင်းကို ဖမ်းယူရာတွင် သိသိသာသာ ကောင်းမွန်ကြောင်း ညွှန်ပြနေသည်။

polynomial ၏ဒီဂရီကို 4 သို့ပြောင်းပါက R နှစ်ထပ်ကိန်းသည် 0.981 သို့ တိုးလာပါသည်။ ၎င်းသည် ဒီဂရီ 3 ကိန်းဂဏန်းများ ဆုတ်ယုတ်မှုပုံစံသည် ဤဒေတာရှိလမ်းကြောင်းကို ဖမ်းယူရန် လုံလောက်သည်ဟု အကြံပြုထားသည်။

ကြိုတင်ခန့်မှန်းကိန်းရှင်၏တန်ဖိုးတစ်ခုပေးထားသည့် တုံ့ပြန်မှုကိန်းရှင်၏မျှော်မှန်းတန်ဖိုးကိုရှာဖွေရန် တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုညီမျှခြင်းကို ကျွန်ုပ်တို့အသုံးပြုနိုင်သည်။ ဥပမာ၊ x = 4 ဆိုရင် y အတွက် မျှော်မှန်းတန်ဖိုးက-

y = 37.2 – 14.2(4) + 2.64(4) ² – 0.126(4) ³ = 14.576

အခြား Google Sheets သင်ခန်းစာများကို ဤစာမျက်နှာတွင် သင်တွေ့နိုင်ပါသည်။