R တွင် polynomial regression (တစ်ဆင့်ပြီးတစ်ဆင့်)

Polynomial regression သည် ကြိုတင်ခန့်မှန်းကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင် သည် linear မဟုတ်သည့်အခါ ကျွန်ုပ်တို့အသုံးပြုနိုင်သည့် နည်းလမ်းတစ်ခုဖြစ်သည်။

ဤဆုတ်ယုတ်မှုအမျိုးအစားသည် ပုံစံယူသည်-

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

h သည် polynomial ၏ “ ဒီဂရီ” ဖြစ်သည်။

ဤသင်ခန်းစာသည် R တွင် polynomial regression လုပ်ဆောင်ပုံအဆင့်ဆင့်ကို ဥပမာပေးထားသည်။

အဆင့် 1: ဒေတာကိုဖန်တီးပါ။

ဤဥပမာအတွက်၊ ကျွန်ုပ်တို့သည် ကျောင်းသား 50 ၏အတန်းတစ်တန်းအတွက် လေ့လာချိန်နာရီအရေအတွက်နှင့် နောက်ဆုံးစာမေးပွဲအဆင့်ပါရှိသော ဒေတာအတွဲတစ်ခုကို ဖန်တီးပါမည်။

 #make this example reproducible
set.seed(1)

#create dataset
df <- data.frame(hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(data)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

အဆင့် 2- ဒေတာကို မြင်ယောင်ကြည့်ပါ။

ဒေတာနှင့် ဆုတ်ယုတ်မှုပုံစံကို အံမကိုက်မီ၊ လေ့လာခဲ့သော နာရီနှင့် စာမေးပွဲရမှတ်အကြား ဆက်စပ်မှုကို မြင်သာစေရန် အပိုင်းအစတစ်ခု ဖန်တီးကြပါစို့။

 library (ggplot2)

ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

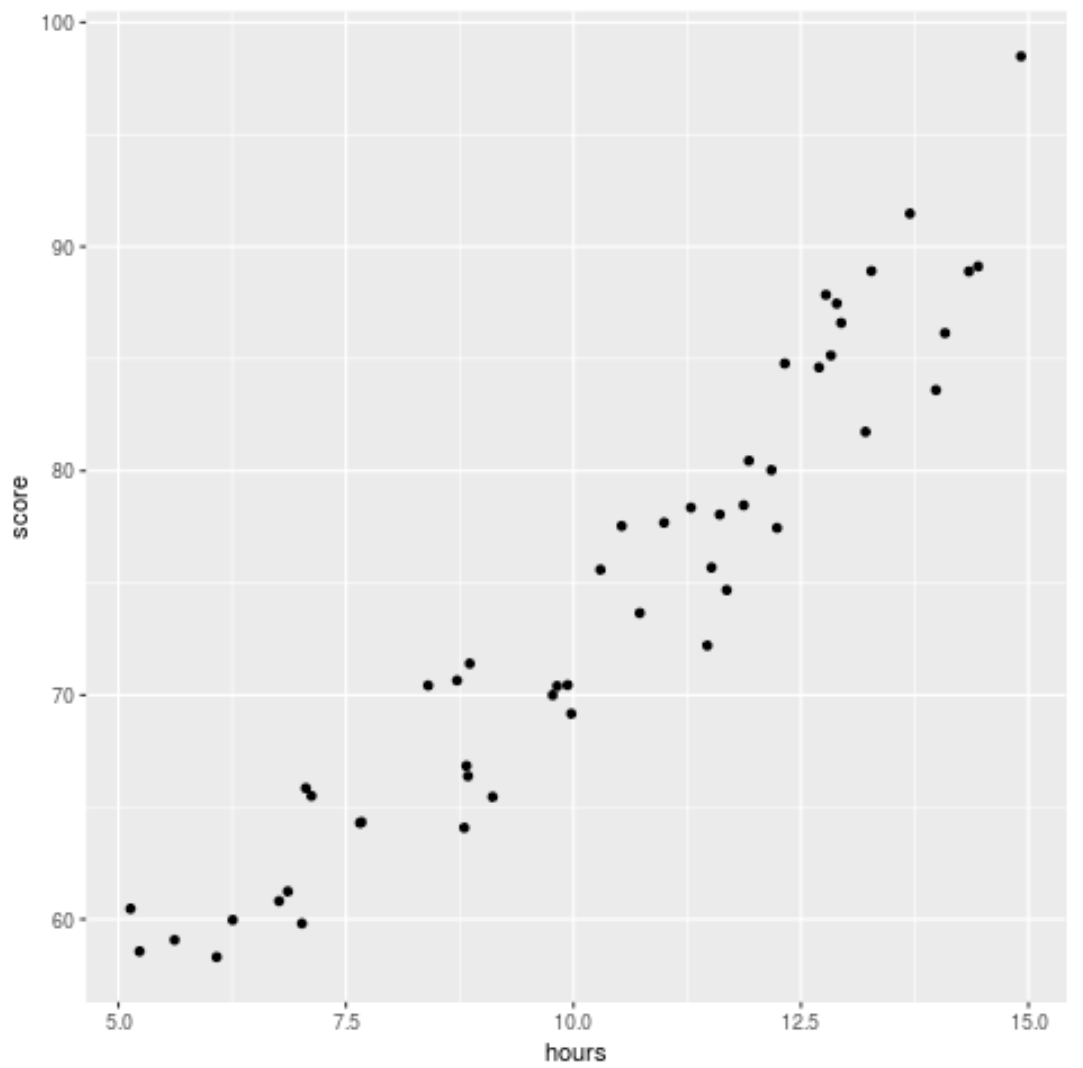
ဒေတာသည် မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းထက် သာလွန်ကောင်းမွန်သော ကိန်းဂဏန်းများ ဆုတ်ယုတ်မှုအား ညွှန်ပြသည်မှာ ဒေတာသည် အနည်းငယ်လေးထောင့်ပုံစံ ဆက်နွယ်မှုရှိကြောင်း ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

အဆင့် 3- polynomial ဆုတ်ယုတ်မှုပုံစံများကို ကွက်တိပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် ဒီဂရီ h = 1…5 ဖြင့် မတူညီသော polynomial regression မော်ဒယ်ငါးခုကို ဖြည့်သွင်းပြီး မော်ဒယ်တစ်ခုစီအတွက် MSE စမ်းသပ်မှုကို တွက်ချက်ရန် k-fold cross-validation ကို k = 10 ကြိမ် အသုံးပြုပါမည်-

 #randomly shuffle data
df.shuffled <- df[ sample ( nrow (df)),]

#define number of folds to use for k-fold cross-validation
K <- 10 

#define degree of polynomials to fit
degree <- 5

#create k equal-sized folds
folds <- cut( seq (1, nrow (df.shuffled)), breaks=K, labels= FALSE )

#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)

#Perform K-fold cross validation
for (i in 1:K){
    
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
    testData <- df.shuffled[testIndexes, ]
    trainData <- df.shuffled[-testIndexes, ]
    
#use k-fold cv to evaluate models
for (j in 1:degree){
        fit.train = lm (score ~ poly (hours,d), data=trainData)
        fit.test = predict (fit.train, newdata=testData)
        mse[i,j] = mean ((fit.test-testData$score)^2) 
    }
}

#find MSE for each degree 
colMeans(mse)

[1] 9.802397 8.748666 9.601865 10.592569 13.545547

ရလဒ်မှ မော်ဒယ်တစ်ခုစီအတွက် MSE စမ်းသပ်မှုကို ကျွန်ုပ်တို့ မြင်တွေ့နိုင်သည်-

• ဒီဂရီ h = 1: 9.80 ဖြင့် MSE စာမေးပွဲ
• ဒီဂရီ h = 2: 8.75 ဖြင့် MSE စာမေးပွဲ
• ဒီဂရီ h = 3: 9.60 ဖြင့် MSE စာမေးပွဲ
• ဒီဂရီ h = 4: 10.59 ဖြင့် MSE စာမေးပွဲ
• ဒီဂရီ h = 5: 13.55 ဖြင့် MSE စာမေးပွဲ

အနိမ့်ဆုံးစမ်းသပ်မှု MSE မော်ဒယ်သည် ဒီဂရီ h = 2 ရှိသော polynomial regression မော်ဒယ်ဖြစ်လာသည်။

၎င်းသည် မူရင်း scatterplot မှ ကျွန်ုပ်တို့၏ ပင်ကိုယ်သဘောနှင့် ကိုက်ညီသည်- လေးပုံတစ်ပုံ ဆုတ်ယုတ်မှုပုံစံသည် ဒေတာနှင့် အသင့်တော်ဆုံးဖြစ်သည်။

အဆင့် 4- နောက်ဆုံးပုံစံကို ပိုင်းခြားစိတ်ဖြာပါ။

နောက်ဆုံးတွင်၊ အကောင်းဆုံးစွမ်းဆောင်ရည်မော်ဒယ်၏ ကိန်းဂဏန်းများကို ကျွန်ုပ်တို့ရရှိနိုင်သည်-

 #fit best model
best = lm (score ~ poly (hours,2, raw= T ), data=df)

#view summary of best model
summary(best)

Call:
lm(formula = score ~ poly(hours, 2, raw = T), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-5.6589 -2.0770 -0.4599 2.5923 4.5122 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) 54.00526 5.52855 9.768 6.78e-13 ***
poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569    
poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ရလဒ်အနေဖြင့်၊ နောက်ဆုံးတပ်ဆင်ထားသောပုံစံကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်-

ရမှတ် = 54.00526 – 0.07904*(နာရီ) + 0.18596*(နာရီ) ²

သင်ကြားသည့်နာရီအရေအတွက်ပေါ်မူတည်၍ ကျောင်းသားတစ်ဦးရရှိမည့်ရမှတ်ကို ခန့်မှန်းရန် ဤညီမျှခြင်းအား ကျွန်ုပ်တို့အသုံးပြုနိုင်ပါသည်။

ဥပမာအားဖြင့်၊ 10 နာရီ စာသင်သော ကျောင်းသားသည် 71.81 အဆင့် ရသင့်သည် ။

ရမှတ် = 54.00526 – 0.07904*(10) + 0.18596*(10) ² = 71.81

ဒေတာအကြမ်း မည်မျှ ကိုက်ညီမှုရှိသည်ကို ကြည့်ရန် တပ်ဆင်ထားသော မော်ဒယ်ကိုလည်း ရေးဆွဲနိုင်သည်-

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

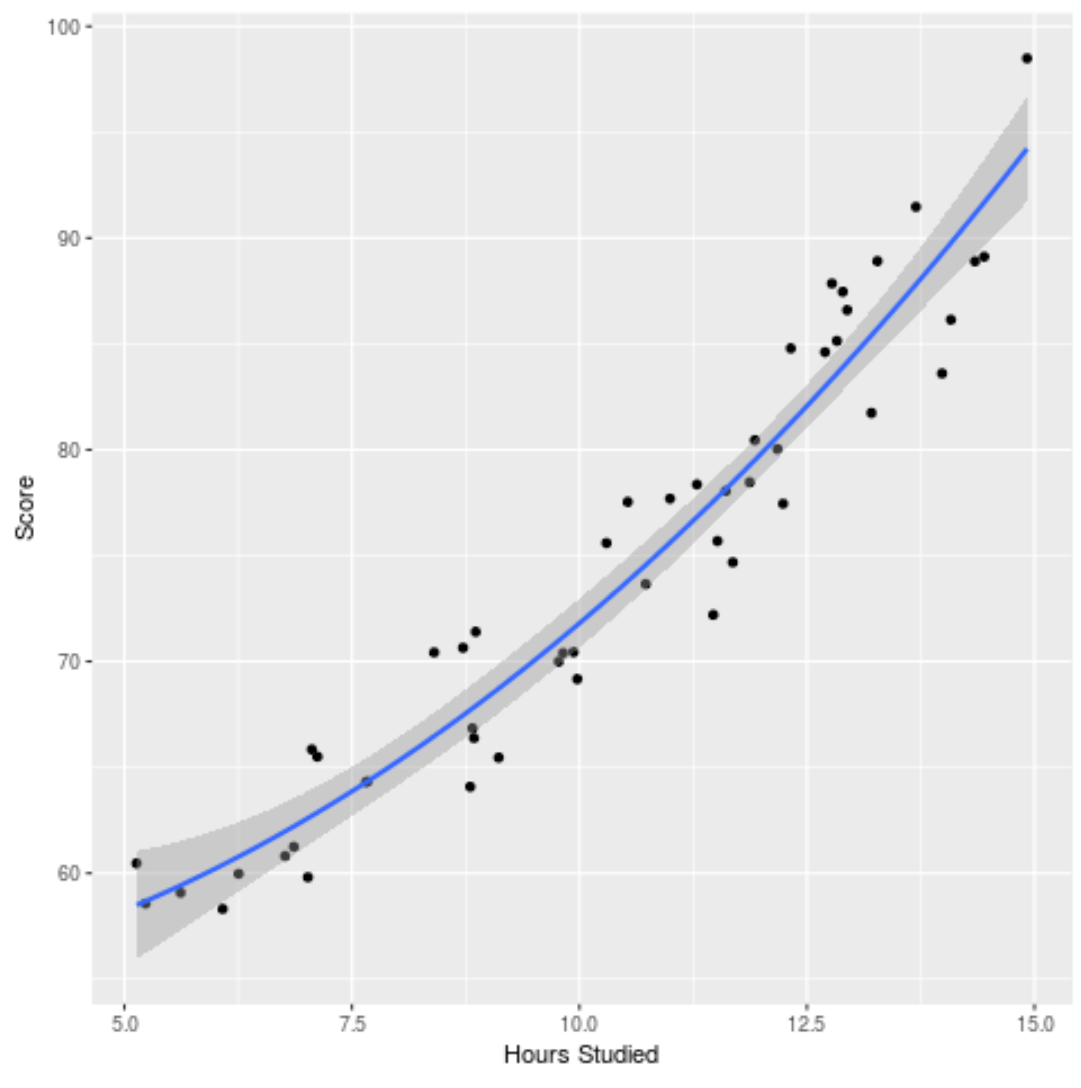
ဤဥပမာတွင်အသုံးပြုထားသော R ကုဒ်အပြည့်အစုံကို ဤနေရာတွင် ရှာတွေ့နိုင်ပါသည်။