Python တွင် polynomial regression လုပ်နည်း

ဆုတ်ယုတ်မှု ခွဲခြမ်းစိတ်ဖြာခြင်းကို တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ရှင်းပြကိန်းရှင်များနှင့် တုံ့ပြန်မှုကိန်းရှင်တို့ကြား ဆက်နွယ်မှုကို အရေအတွက်သတ်မှတ်ရန်အတွက် အသုံးပြုသည်။

ဆုတ်ယုတ်မှုခွဲခြမ်းစိတ်ဖြာမှု၏ အသုံးအများဆုံးအမျိုးအစားမှာ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှု ဖြစ်ပြီး၊ ခန့်မှန်းသူကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်သည် မျဉ်းကြောင်းဆက်စပ်မှုရှိသည့်အခါ အသုံးပြုသည်။

သို့သော် တစ်ခါတစ်ရံတွင် ကြိုတင်ခန့်မှန်းကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်ကြား ဆက်ဆံရေးသည် လိုင်းမဟုတ်ပေ။

ဥပမာအားဖြင့်၊ စစ်မှန်သောဆက်ဆံရေးသည် လေးထောင့်ပုံဖြစ်နိုင်သည်-

သို့မဟုတ် ၎င်းသည် ကုဗိလ်ဖြစ်နိုင်သည်။

ဤကိစ္စများတွင်၊ ကိန်းရှင်များကြားတွင် linear မဟုတ်သော ဆက်နွယ်မှုကို တွက်ချက်နိုင်သည့် polynomial regression ကို အသုံးပြုခြင်းသည် အဓိပ္ပါယ်ရှိစေသည်။

ဤသင်ခန်းစာတွင် Python တွင် polynomial regression လုပ်နည်းကို ရှင်းပြထားသည်။

ဥပမာ- Python ရှိ Polynomial Regression

Python တွင် အောက်ပါ ခန့်မှန်းချက် ကိန်းရှင် (x) နှင့် တုံ့ပြန်မှု ကိန်းရှင် (y) ရှိသည် ဆိုပါစို့။

 x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]
y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]

ဤဒေတာ၏ ရိုးရှင်းသော ခွဲခြမ်းစိပ်ဖြာမှုတစ်ခုကို ဖန်တီးပါက၊ x နှင့် y အကြား ဆက်နွယ်မှုမှာ linear မဟုတ်ကြောင်း ရှင်းရှင်းလင်းလင်း သိမြင်နိုင်သည်-

 import matplotlib.pyplot as plt

#create scatterplot 
plt.scatter(x, y)

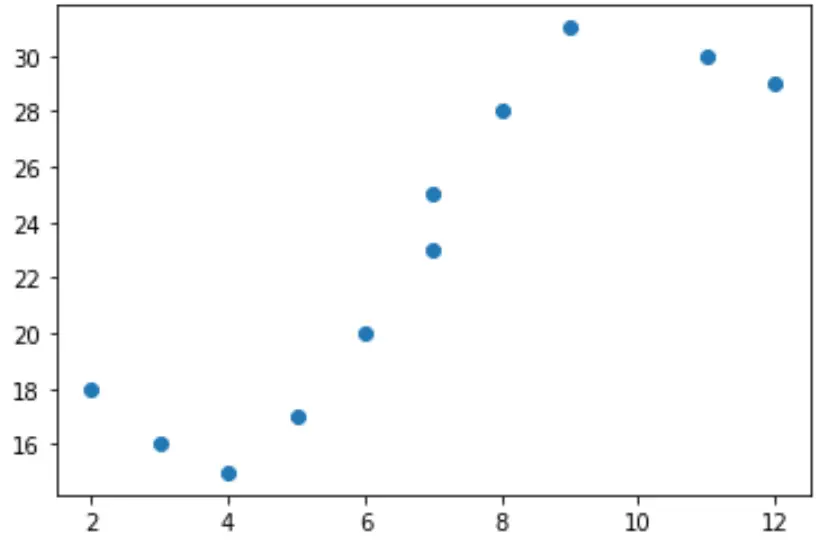
ထို့ကြောင့် ဤဒေတာအတွက် linear regression model ကို ကိုက်ညီရန် အဓိပ္ပါယ်မရှိပေ။ ယင်းအစား၊ numpy.polyfit() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ ဒီဂရီ 3 နှင့် polynomial ဆုတ်ယုတ်မှုပုံစံကို အံဝင်ခွင်ကျဖြစ်အောင် ကြိုးပမ်းနိုင်သည်-

 import numpy as np

#polynomial fit with degree = 3
model = np.poly1d(np.polyfit(x, y, 3))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 12, 50)
plt.scatter(x, y)
plt.plot(polyline, model(polyline))
plt.show() 

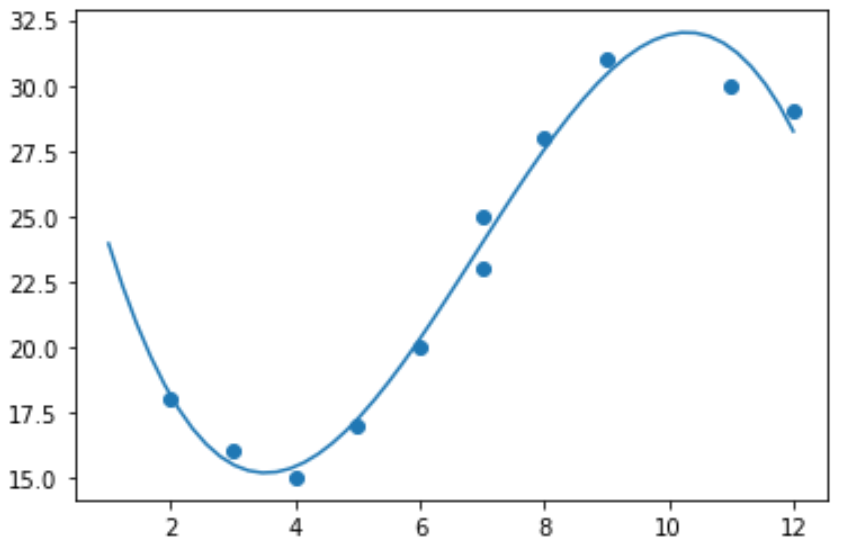
မော်ဒယ် coefficients ကို ရိုက်နှိပ်ခြင်းဖြင့် တပ်ဆင်ထားသော polynomial regression equation ကို ရယူနိုင်ပါသည်။

 print(model)

poly1d([ -0.10889554, 2.25592957, -11.83877127, 33.62640038])

တပ်ဆင်ထားသော polynomial ဆုတ်ယုတ်မှုညီမျှခြင်းမှာ-

y = -0.109x ³ + 2.256x ² – 11.839x + 33.626

ဤညီမျှခြင်းအား ရှင်းလင်းချက်ကိန်းရှင်၏ ပေးထားသောတန်ဖိုးတစ်ခုပေးထားသည့် တုံ့ပြန်မှုကိန်းရှင်၏မျှော်မှန်းတန်ဖိုးကို ရှာဖွေရန် အသုံးပြုနိုင်သည်။

ဥပမာ၊ x = 4 ဟုယူဆပါ။ တုံ့ပြန်မှုကိန်းရှင်အတွက် မျှော်မှန်းတန်ဖိုးမှာ y ဖြစ်လိမ့်မည်-

y = -0.109(4) ³ + 2.256(4) ² – 11.839(4) + 33.626= 15.39 ။

မော်ဒယ်၏ R-squared ကိုရရန် အတိုချုံးရေးနိုင်သည်၊ ၎င်းသည် ခန့်မှန်းသူကိန်းရှင်များဖြင့် ရှင်းပြနိုင်သော တုံ့ပြန်မှုကိန်းရှင်ရှိ ကွဲလွဲမှု၏အချိုးအစားဖြစ်သည်။

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = numpy.polyfit(x, y, degree)
    p = numpy.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = numpy.sum(y)/len(y)
    ssreg = numpy.sum((yhat-ybar)**2)
    sstot = numpy.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(x, y, 3)

{'r_squared': 0.9841113454245183}

ဤဥပမာတွင်၊ မော်ဒယ်၏ R စတုရန်းသည် 0.9841 ဖြစ်သည်။

ဆိုလိုသည်မှာ တုံ့ပြန်မှုကိန်းရှင်၏ 98.41% သည် ကြိုတင်ခန့်မှန်းကိန်းရှင်များဖြင့် ရှင်းပြနိုင်သည်။