Python တွင် ကျောင်းသားဖြစ်ထားသော အကြွင်းအကျန်များကို တွက်ချက်နည်း

ကျောင်းသားအကြွင်းအကျန် သည် ၎င်း၏ခန့်မှန်းစံသွေဖည်မှုဖြင့် ပိုင်းခြားထားသော အကြွင်းတစ်ခုဖြစ်သည်။

လက်တွေ့တွင်၊ ကျောင်းသားအကြွင်းအကျန်သည် 3 ၏ ပကတိတန်ဖိုးထက် ပိုများသော ဒေတာအတွဲတစ်ခုတွင် စောင့်ကြည့်မှု တိုင်းသည် သာလွန်သည်ဟု ကျွန်ုပ်တို့ယေဘုယျအားဖြင့် ဆိုကြသည်။

အောက်ပါ syntax ကိုအသုံးပြုသည့် statsmodels ၏ OLSResults.outlier_test() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ Python ရှိ ဆုတ်ယုတ်မှုပုံစံ၏ ကျောင်းသားဖြစ်ကျန်နေသေးသော အကြွင်းအကျန်များကို ကျွန်ုပ်တို့ အမြန်ရနိုင်သည်-

OLSResults.outlier_test()

OLSResults သည် statsmodels ols() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ ကိုက်ညီသော linear model တစ်ခု၏ အမည်ဖြစ်သည်။

ဥပမာ- Python တွင် ကျောင်းသားဖြစ်ကျန်နေသေးသော တွက်ချက်မှု

Python တွင် အောက်ပါ ရိုးရှင်းသော linear regression model ကို ကျွန်ုပ်တို့တည်ဆောက်သည်ဆိုပါစို့။

 #import necessary packages and functions
import numpy as np
import pandas as pd
import statsmodels. api as sm
from statsmodels. formula . api import ols

#create dataset
df = pd. DataFrame ({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19]})

#fit simple linear regression model
model = ols('rating ~ points', data=df). fit ()

ဒေတာအတွဲတွင် လေ့လာမှုတစ်ခုစီအတွက် ကျောင်းသားဖြစ်ကျန်နေသေးသော DataFrame တစ်ခုထုတ်လုပ်ရန် outlier_test() လုပ်ဆောင်ချက်ကို ကျွန်ုပ်တို့အသုံးပြုနိုင်သည်-

 #calculate studentized residuals
stud_res = model. outlier_test ()

#display studentized residuals
print(stud_res)

    student_resid unadj_p bonf(p)
0 -0.486471 0.641494 1.000000
1 -0.491937 0.637814 1.000000
2 0.172006 0.868300 1.000000
3 1.287711 0.238781 1.000000
4 0.106923 0.917850 1.000000
5 0.748842 0.478355 1.000000
6 -0.968124 0.365234 1.000000
7 -2.409911 0.046780 0.467801
8 1.688046 0.135258 1.000000
9 -0.014163 0.989095 1.000000

ဤ DataFrame သည် dataset တွင်ကြည့်ရှုမှုတစ်ခုစီအတွက်အောက်ပါတန်ဖိုးများကိုပြသသည်-

• ကျောင်သားအကြွင်းအကျန်
• ကျောင်းသားအဖြစ်မှ ကျန်ရှိသော p-value ကို ချိန်ညှိမထားသော p-value
• ကျန်ရှိသော ကျောင်းသား၏ Bonferroni-ပြင်ဆင်ထားသော p-တန်ဖိုး

ဒေတာအတွဲတွင် ပထမလေ့လာချက်အတွက် ကျောင်းသားဖြစ်ကျန်ကျန်သည် -0.486471 ၊ ဒုတိယလေ့လာရေးအတွက် ကျောင်းသားကျန်ကျန်သည် -0.491937 စသည်တို့ဖြစ်သည်။

သက်ဆိုင်သော ကျောင်းသားပြုထားသော အကြွင်းအကျန်များနှင့် ပတ်သက်သော ကြိုတင်ခန့်မှန်းကိန်းရှင်များ၏ တန်ဖိုးများကို အမြန်ကွက်ကွက် ဖန်တီးနိုင်သည်။

 import matplotlib. pyplot as plt

#define predictor variable values and studentized residuals
x = df[' points ']
y = stud_res[' student_resid ']

#create scatterplot of predictor variable vs. studentized residuals
plt. scatter (x,y)
plt. axhline (y=0, color=' black ', linestyle=' -- ')
plt. xlabel (' Points ')
plt. ylabel (' Studentized Residuals ') 

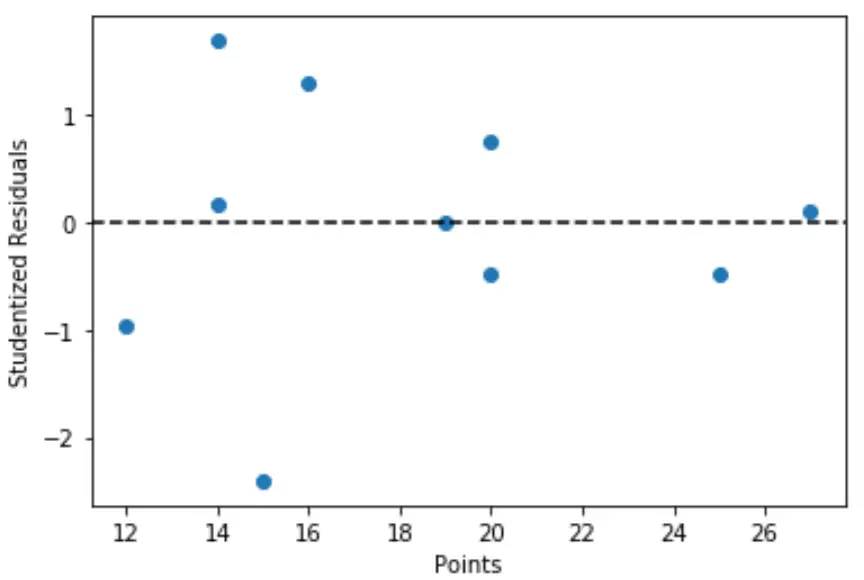
ဂရပ်မှလေ့လာတွေ့ရှိချက်များတွင် 3 ထက်ကြီးသော ပကတိတန်ဖိုးရှိသော ကျောင်းသားအကြွင်းအကျန်မရှိသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်၊ ထို့ကြောင့် ဒေတာအတွဲတွင် ရှင်းရှင်းလင်းလင်းအစွန်းအထင်းများမရှိပါ။

ထပ်လောင်းအရင်းအမြစ်များ

Python တွင် ရိုးရှင်းသော linear regression လုပ်နည်း
Python တွင် မျဉ်းကြောင်း ဆုတ်ယုတ်မှု အများအပြား လုပ်ဆောင်နည်း
Python တွင် Residual Plot ဖန်တီးနည်း