Python တွင် covariance matrix ဖန်တီးနည်း
Covariance သည် ကိန်းရှင်တစ်ခုရှိ ပြောင်းလဲမှုများနှင့် ဒုတိယကိန်းရှင်တစ်ခုရှိ အပြောင်းအလဲများနှင့် ဆက်စပ်နေပုံကို တိုင်းတာခြင်းဖြစ်သည်။ ပို၍တိကျသည်မှာ၊ ၎င်းသည် ကိန်းရှင်နှစ်ခုအား မျဉ်းသားဆက်စပ်နေသည့်အတိုင်းအတာကို တိုင်းတာခြင်းဖြစ်သည်။
covariance matrix သည် မတူညီသော variable များစွာကြားတွင် ကွဲလွဲမှုကိုပြသသော စတုရန်း matrix တစ်ခုဖြစ်သည်။ ၎င်းသည် ဒေတာအတွဲတစ်ခုတွင် မတူညီသော variable များ မည်သို့ဆက်စပ်ကြောင်း နားလည်ရန် အသုံးဝင်သောနည်းလမ်းတစ်ခုဖြစ်သည်။
အောက်ဖော်ပြပါ ဥပမာသည် Python တွင် ကွဲပြားသည့် matrix တစ်ခုကို ဖန်တီးနည်းကို ပြသထားသည်။
Python တွင် Covariance Matrix ဖန်တီးနည်း
Python တွင် ကွဲပြားမှုမက်ထရစ်တစ်ခုကို ဖန်တီးရန် အောက်ပါအဆင့်များကို အသုံးပြုပါ။
အဆင့် 1: ဒေတာအတွဲကို ဖန်တီးပါ။
ပထမဦးစွာ၊ သင်္ချာ၊ သိပ္ပံနှင့် သမိုင်းဘာသာရပ်သုံးခုတွင် မတူညီသော ကျောင်းသား ၁၀ ဦး၏ စာမေးပွဲရမှတ်များပါဝင်သော ဒေတာအတွဲတစ်ခုကို ဖန်တီးပါမည်။
import numpy as np math = [84, 82, 81, 89, 73, 94, 92, 70, 88, 95] science = [85, 82, 72, 77, 75, 89, 95, 84, 77, 94] history = [97, 94, 93, 95, 88, 82, 78, 84, 69, 78] data = np.array([math, science, history])
အဆင့် 2- ကွဲပြားမှု matrix ကို ဖန်တီးပါ။
ထို့နောက်၊ ကျွန်ုပ်တို့သည် numpy cov() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ ဤဒေတာအတွဲအတွက် covariance matrix ကို ဖန်တီးပြီး ထို bias = True ကို သတ်မှတ်ခြင်းဖြင့် လူဦးရေ ကွဲလွဲမှုမက်ထရစ်ကို တွက်ချက်နိုင်မည်ဖြစ်သည်။
np.cov(data, bias= True )
array([[ 64.96, 33.2, -24.44],
[33.2, 56.4, -24.1],
[-24.44, -24.1, 75.56]])
အဆင့် 3- ကွဲပြားမှုမက်ထရစ်ကို အဓိပါယ်ဖွင့်ဆိုပါ။
matrix ၏ထောင့်ဖြတ်များတစ်လျှောက်ရှိတန်ဖိုးများသည် ဘာသာရပ်တစ်ခုစီ၏ကွဲလွဲမှုများဖြစ်သည်။ ဥပမာအားဖြင့်:
- သင်္ချာရမှတ်များ၏ ကွဲလွဲမှုသည် 64.96 ဖြစ်သည်။
- သိပ္ပံရမှတ်များ၏ ကွဲလွဲမှုသည် 56.4 ဖြစ်သည်။
- သမိုင်းဝင်ရမှတ်ကွဲလွဲမှုသည် 75.56 ဖြစ်သည်။
matrix ၏အခြားတန်ဖိုးများသည် မတူညီသောဘာသာရပ်များအကြား ကွဲလွဲမှုများကို ကိုယ်စားပြုသည်။ ဥပမာအားဖြင့်:
- သင်္ချာနှင့် သိပ္ပံရမှတ်များအကြား ကွာခြားချက်မှာ ၃၃.၂ ဖြစ်သည်။
- သင်္ချာနှင့် သမိုင်းရမှတ်များကြား ကွဲလွဲမှုမှာ -24.44 ဖြစ်သည်။
- သိပ္ပံနှင့် သမိုင်းရမှတ်များအကြား ကွဲလွဲမှုမှာ -24.1 ဖြစ်သည်။
ကွဲလွဲမှုများအတွက် အပြုသဘောဆောင်သော ကိန်းဂဏန်း တစ်ခုသည် ကိန်းရှင်နှစ်ခုသည် တပြိုင်နက်တွင် အတိုး သို့မဟုတ် လျော့တတ်သည်ကို ညွှန်ပြသည်။ ဥပမာအားဖြင့်၊ သင်္ချာနှင့် သိပ္ပံတွင် အပြုသဘောဆောင်သော ကွဲလွဲမှု (33.2) ရှိသည်၊ သင်္ချာတွင် အမှတ်များသော ကျောင်းသားများသည်လည်း သိပ္ပံတွင် ရမှတ်များတတ်ကြောင်း ညွှန်ပြသည်။ အပြန်အလှန်အားဖြင့် သင်္ချာဘာသာရပ်တွင် ညံ့ဖျင်းသော ကျောင်းသားများသည် သိပ္ပံဘာသာရပ်တွင် ညံ့ဖျင်းလေ့ရှိသည်။
ကွဲလွဲမှုတစ်ခုအတွက် အနုတ်ကိန်းဂဏန်း တစ်ခုသည် ကိန်းရှင်တစ်ခုတိုးလာသည်နှင့်အမျှ၊ ဒုတိယကိန်းရှင်သည် လျော့နည်းသွားကြောင်း ဖော်ပြသည်။ ဥပမာအားဖြင့်၊ သင်္ချာနှင့် သမိုင်းတွင် အနုတ်လက္ခဏာ ကွာဟချက် (-24.44) ရှိသည်၊ သင်္ချာတွင် အမှတ်များသော ကျောင်းသားများသည် သမိုင်းတွင် အမှတ်နိမ့်တတ်ကြောင်း ညွှန်ပြသည်။ ဆန့်ကျင်ဘက်အားဖြင့် သင်္ချာဘာသာရပ်တွင် အမှတ်နိမ့်သော ကျောင်းသားများသည် သမိုင်းတွင် ရမှတ်မြင့်မားလေ့ရှိသည်။
အဆင့် 4- ကွဲပြားမှုမက်ထရစ်ကို မြင်ယောင်ကြည့်ပါ (ချန်လှပ်ထားနိုင်သည်)။
seaborn package ၏ heatmap() function ကို အသုံးပြု၍ တူညီသော matrix ကို မြင်ယောင်နိုင်သည်-
import seaborn as sns import matplotlib.pyplot as plt cov = np.cov(data, bias=True) labs = ['math', 'science', 'history'] sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs) plt.show()
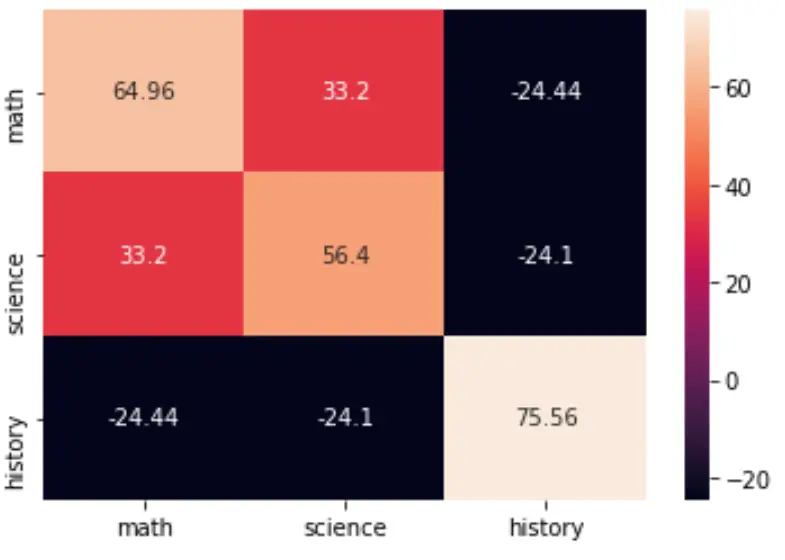
cmap အငြင်းအခုံကို သတ်မှတ်ခြင်းဖြင့် အရောင် palette ကိုလည်း ပြောင်းလဲနိုင်သည်။
sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs, cmap=' YlGnBu ')
plt.show()
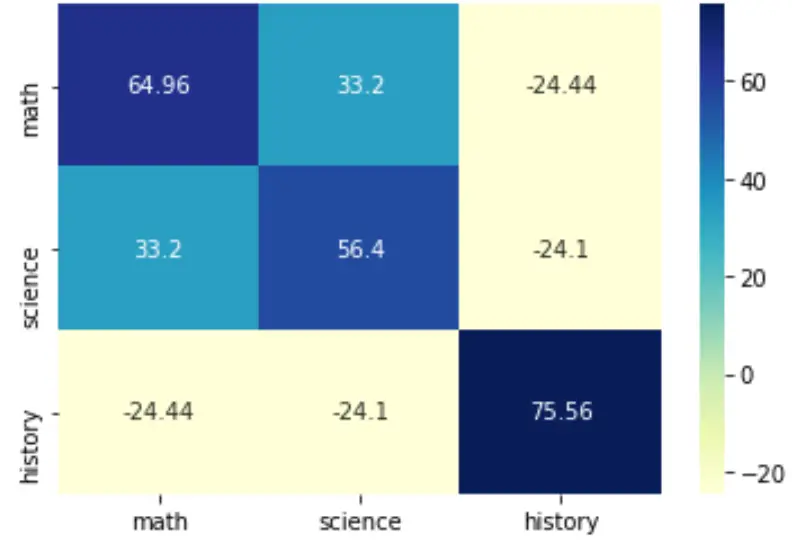
ဤအပူမြေပုံပုံစံပြုလုပ်ပုံနှင့်ပတ်သက်၍ နောက်ထပ်အသေးစိတ်အချက်အလက်များအတွက်၊ ပင်လယ်တွင်းရှိ စာရွက်စာတမ်းများ ကို ကိုးကားပါ။