Python တွင် normality ကိုစမ်းသပ်နည်း (နည်းလမ်း 4 ခု)

ကိန်းဂဏန်းစစ်ဆေးမှုများစွာသည် ဒေတာအစုံများကို ပုံမှန်ဖြန့်ဝေသည်ဟု ယူဆသည် ။

Python တွင် ဤယူဆချက်ကို စစ်ဆေးရန် ဘုံနည်းလမ်းလေးခုရှိသည်။

1. (အမြင်နည်းလမ်း) ဟီစတိုဂရမ်တစ်ခု ဖန်တီးပါ။

• ဟီစတိုဂရမ်သည် ခန့်မှန်းခြေအားဖြင့် “ ခေါင်းလောင်း” ပုံသဏ္ဍာန်ဖြစ်ပါက၊ ဒေတာကို ပုံမှန်အတိုင်း ဖြန့်ဝေသည်ဟု ယူဆပါသည်။

2. (Visual method) QQ ကွက်ကွက်ဖန်တီးပါ။

• ကွက်လပ်ပေါ်ရှိ အမှတ်များသည် ဖြောင့်ထောင့်ဖြတ်မျဉ်းတစ်လျှောက် အကြမ်းဖျင်းအားဖြင့် တည်ရှိနေပါက ဒေတာကို ပုံမှန်အတိုင်း ဖြန့်ဝေသည်ဟု ယူဆပါသည်။

3. (တရားဝင်စာရင်းအင်းစမ်းသပ်မှု) Shapiro-Wilk စမ်းသပ်မှုပြုလုပ်ပါ။

• စမ်းသပ်မှု၏ p-value သည် α = 0.05 ထက် ကြီးပါက ဒေတာကို ပုံမှန်အတိုင်း ဖြန့်ဝေသည်ဟု ယူဆပါသည်။

4. (တရားဝင်စာရင်းအင်းစမ်းသပ်မှု) Kolmogorov-Smirnov စမ်းသပ်မှုပြုလုပ်ပါ။

• စမ်းသပ်မှု၏ p-value သည် α = 0.05 ထက် ကြီးပါက ဒေတာကို ပုံမှန်အတိုင်း ဖြန့်ဝေသည်ဟု ယူဆပါသည်။

အောက်ဖော်ပြပါ ဥပမာများသည် ဤနည်းလမ်းတစ်ခုစီကို လက်တွေ့အသုံးချနည်းကို ပြသထားသည်။

နည်းလမ်း 1- Histogram ဖန်တီးပါ။

အောက်ပါကုဒ်သည် မှတ်တမ်း-ပုံမှန်ဖြန့်ဝေမှု နောက်ဆက်တွဲ ဒေတာအတွဲတစ်ခုအတွက် ဟီစတိုဂရမ်ကို ဖန်တီးနည်းကို ပြသသည်-

 import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20) 

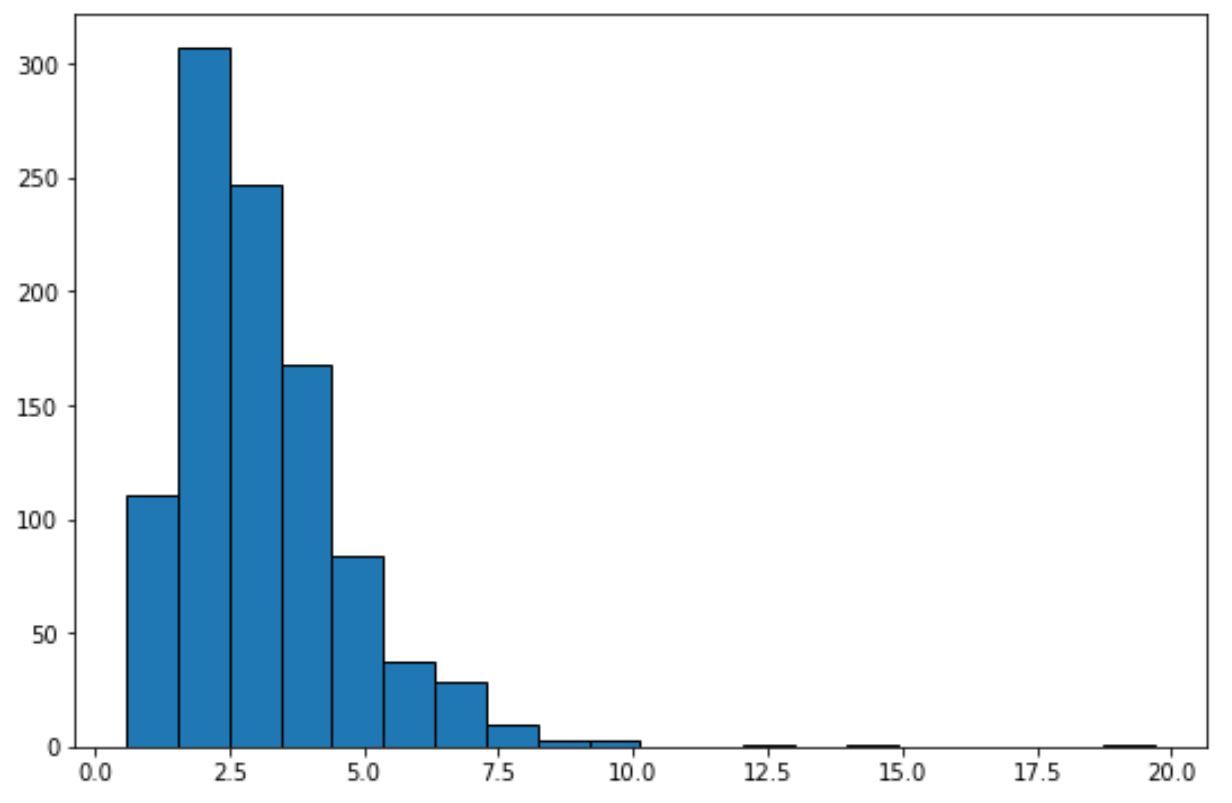
ဤဟစ်စတိုဂရမ်ကိုကြည့်ခြင်းဖြင့် ဒေတာအတွဲသည် “ခေါင်းလောင်းပုံသဏ္ဍာန်” မပြဘဲ ပုံမှန်ဖြန့်ဝေခြင်းမရှိကြောင်း ကျွန်ုပ်တို့ပြောပြနိုင်ပါသည်။

နည်းလမ်း 2- QQ Plot တစ်ခုဖန်တီးပါ။

အောက်ပါ ကုဒ်သည် မှတ်တမ်း-ပုံမှန် ဖြန့်ဝေမှုနောက်ဆက်တွဲ ဒေတာအတွဲတစ်ခုအတွက် QQ ကွက်ကွက် ဖန်တီးနည်းကို ပြသသည်-

 import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')

plt. show ()

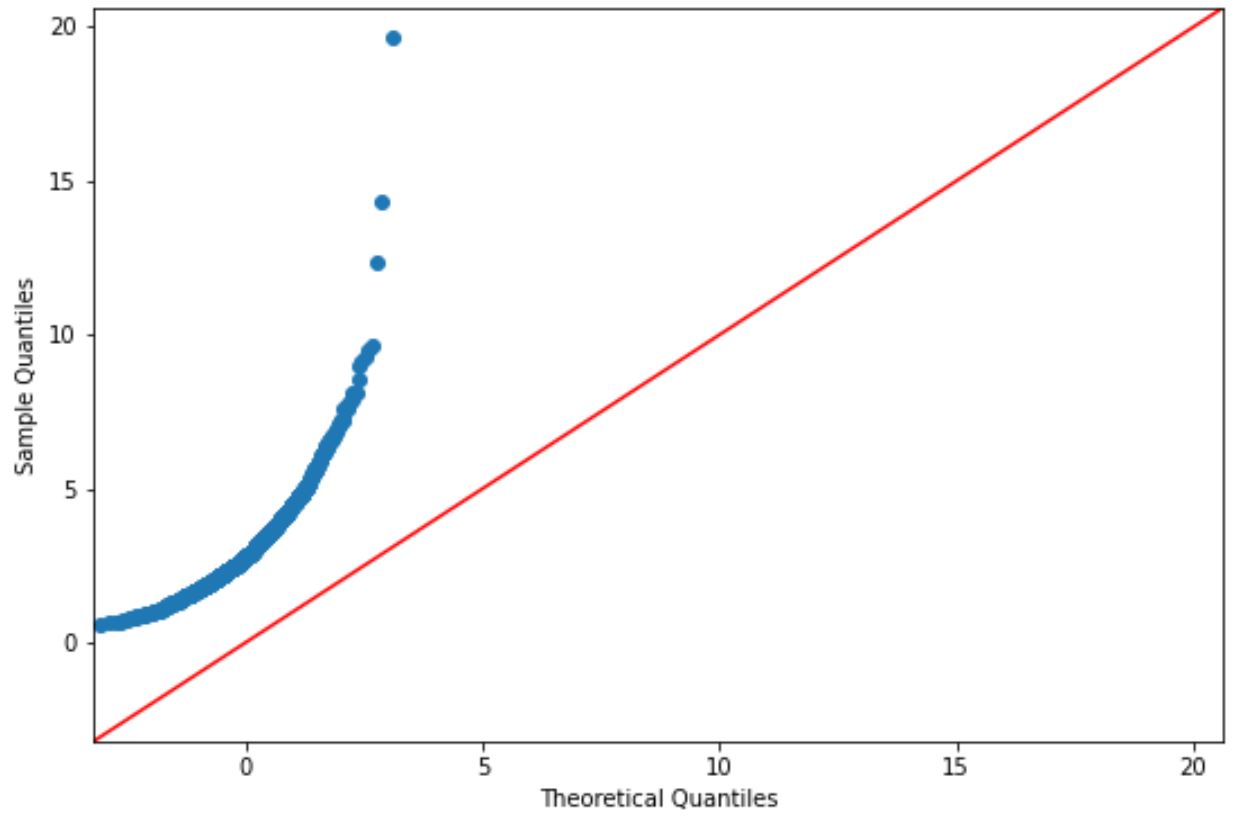
ကွက်ကွက်အမှတ်များသည် ဖြောင့်ထောင့်ဖြတ်မျဉ်းတစ်လျှောက် ခန့်မှန်းခြေအားဖြင့် တည်ရှိနေပါက၊ ဒေတာအစုံကို ပုံမှန်အားဖြင့် ဖြန့်ဝေသည်ဟု ကျွန်ုပ်တို့ ယေဘူယျအားဖြင့် ယူဆပါသည်။

သို့သော်၊ ဤဂရပ်ပေါ်ရှိ အမှတ်များသည် အနီရောင်မျဉ်းနှင့် မကိုက်ညီသောကြောင့် ဤဒေတာအတွဲကို ပုံမှန်ဖြန့်ဝေသည်ဟု ကျွန်ုပ်တို့ ယူဆ၍မရပါ။

လော့ဂ်-ပုံမှန်ဖြန့်ဝေမှုလုပ်ဆောင်ချက်ကို အသုံးပြု၍ ဒေတာကို ထုတ်ပေးခဲ့ခြင်းကြောင့် ၎င်းသည် အဓိပ္ပာယ်ရှိသင့်သည်။

နည်းလမ်း 3- Shapiro-Wilk စမ်းသပ်မှုပြုလုပ်ပါ။

အောက်ပါကုဒ်သည် မှတ်တမ်း-ပုံမှန်ဖြန့်ဝေမှုနောက်ဆက်တွဲ ဒေတာအတွဲအတွက် Shapiro-Wilk ကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-

 import math
import numpy as np
from scipy.stats import shapiro 
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)

ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)

ရလဒ်မှ၊ စမ်းသပ်စာရင်းအင်းသည် 0.857 ဖြစ်ပြီး သက်ဆိုင်သော p-value သည် 3.88e-29 (သုညနှင့် အလွန်နီးစပ်သည်) ကို တွေ့နိုင်ပါသည်။

p-value သည် 0.05 ထက်နည်းသောကြောင့် Shapiro-Wilk test ၏ null hypothesis ကို ငြင်းပယ်ပါသည်။

ဆိုလိုသည်မှာ နမူနာဒေတာသည် သာမန်ဖြန့်ဝေမှုမှ လာခြင်းမရှိဟု ဆိုရန် လုံလောက်သော အထောက်အထားရှိသည်။

နည်းလမ်း 4- Kolmogorov-Smirnov စမ်းသပ်မှုပြုလုပ်ပါ။

အောက်ပါ ကုဒ်သည် မှတ်တမ်း-ပုံမှန် ဖြန့်ဝေမှုနောက်ဆက်တွဲ ဒေတာအတွဲအတွက် Kolmogorov-Smirnov စမ်းသပ်မှုအား မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-

 import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')

KstestResult(statistic=0.84125708308077, pvalue=0.0)

ရလဒ်မှ၊ စမ်းသပ်စာရင်းအင်းသည် 0.841 ဖြစ်ပြီး သက်ဆိုင်ရာ p-value သည် 0.0 ဖြစ်သည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

p-value သည် 0.05 ထက်နည်းသောကြောင့်၊ Kolmogorov-Smirnov test ၏ null hypothesis ကို ငြင်းပယ်ပါသည်။

ဆိုလိုသည်မှာ နမူနာဒေတာသည် သာမန်ဖြန့်ဝေမှုမှ လာခြင်းမရှိဟု ဆိုရန် လုံလောက်သော အထောက်အထားရှိသည်။

ပုံမှန်မဟုတ်သောဒေတာကို ကိုင်တွယ်နည်း

ပေးထားသည့် ဒေတာအစုံကို ပုံမှန်အတိုင်း ဖြန့်ဝေခြင်း မရှိပါက ၊ ၎င်းကို ပုံမှန်အတိုင်း ပိုမိုဖြန့်ဝေနိုင်စေရန် အောက်ပါအသွင်ပြောင်းမှုများထဲမှ တစ်ခုကို ကျွန်ုပ်တို့ မကြာခဏ လုပ်ဆောင်နိုင်သည်-

1. မှတ်တမ်းအသွင်ပြောင်းခြင်း- x တန်ဖိုးများကို log(x) သို့ ပြောင်းလဲပါ။

2. Square root အသွင်ပြောင်းခြင်း- x မှ √x တန်ဖိုးများကို ပြောင်းပါ။

3. Cube root အသွင်ပြောင်းခြင်း- x မှ x ^1/3 တန်ဖိုးများကို ပြောင်းလဲပါ။

ဤအသွင်ပြောင်းမှုများကို လုပ်ဆောင်ခြင်းဖြင့် ဒေတာအတွဲသည် ယေဘူယျအားဖြင့် ပိုမိုပုံမှန်အတိုင်း ဖြန့်ဝေလာပါသည်။

Python တွင် ဤအသွင်ပြောင်းမှုများကို မည်သို့လုပ်ဆောင်ရမည်ကို ကြည့်ရှုရန် ဤသင်ခန်းစာကို ဖတ်ပါ။