Python တွင် multidimensional scaling လုပ်နည်း

စာရင်းဇယားများတွင်၊ ဘက်စုံစကေးချဲ့ခြင်းသည် စိတ္တဇ Cartesian space (များသောအားဖြင့် 2D အာကာသ) ရှိ ဒေတာအတွဲတစ်ခုရှိ စူးစမ်းလေ့လာမှုများ၏ တူညီမှုကို မြင်သာစေရန် နည်းလမ်းတစ်ခုဖြစ်သည်။

Python တွင် multidimensional scaling လုပ်ရန် အလွယ်ကူဆုံးနည်းလမ်းမှာ sklearn.manifold submodule ၏ MDS() function ကို အသုံးပြုရန်ဖြစ်သည်။

အောက်ဖော်ပြပါ ဥပမာသည် ဤလုပ်ဆောင်ချက်ကို လက်တွေ့အသုံးချနည်းကို ပြသထားသည်။

ဥပမာ- Python တွင် Multidimensional Scaling

အမျိုးမျိုးသော ဘတ်စကတ်ဘောကစားသမားများအကြောင်း အချက်အလက်ပါရှိသော အောက်ပါပန်ဒါ DataFrame ရှိသည်ဆိုပါစို့။

 import pandas as pd

#create DataFrane
df = pd. DataFrame ({' player ': ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K '],
                   ' points ': [4, 4, 6, 7, 8, 14, 16, 19, 25, 25, 28],
                   ' assists ': [3, 2, 2, 5, 4, 8, 7, 6, 8, 10, 11],
                   ' blocks ': [7, 3, 6, 7, 5, 8, 8, 4, 2, 2, 1],
                   ' rebounds ': [4, 5, 5, 6, 5, 8, 10, 4, 3, 2, 2]})

#set player column as index column
df = df. set_index (' player ')

#view Dataframe
print (df)

        points assists blocks rebounds
player                                   
A 4 3 7 4
B 4 2 3 5
C 6 2 6 5
D 7 5 7 6
E 8 4 5 5
F 14 8 8 8
G 16 7 8 10
H 19 6 4 4
I 25 8 2 3
D 25 10 2 2
K 28 11 1 2

ကျွန်ုပ်တို့သည် sklearn.manifold module ၏ MDS() လုပ်ဆောင်ချက်ဖြင့် ဘက်စုံစကေးချဲ့ရန်အတွက် အောက်ပါကုဒ်ကို အသုံးပြုနိုင်ပါသည်။

 from sklearn. manifold import MDS

#perform multi-dimensional scaling
mds = MDS(random_state= 0 )
scaled_df = mds. fit_transform (df)

#view results of multi-dimensional scaling
print (scaled_df)

[[ 7.43654469 8.10247222]
 [4.13193821 10.27360901]
 [5.20534681 7.46919526]
 [6.22323046 4.45148627]
 [3.74110999 5.25591459]
 [3.69073384 -2.88017811]
 [3.89092087 -5.19100988]
 [ -3.68593169 -3.0821144 ]
 [ -9.13631889 -6.81016012]
 [ -8.97898385 -8.50414387]
 [-12.51859044 -9.08507097]]

မူရင်း DataFrame ၏အတန်းတစ်ခုစီကို (x၊ y) သြဒိနိတ်တစ်ခုသို့ လျှော့ချထားသည်။

2D space တွင် ဤသြဒိနိတ်များကို မြင်သာစေရန် အောက်ပါကုဒ်ကို အသုံးပြုနိုင်ပါသည်။

 import matplotlib.pyplot as plt

#create scatterplot
plt. scatter (scaled_df[:,0], scaled_df[:,1])

#add axis labels
plt. xlabel (' Coordinate 1 ')
plt. ylabel (' Coordinate 2 ')

#add lables to each point
for i, txt in enumerate( df.index ):
    plt. annotate (txt, (scaled_df[:,0][i]+.3, scaled_df[:,1][i]))

#display scatterplot
plt. show ()

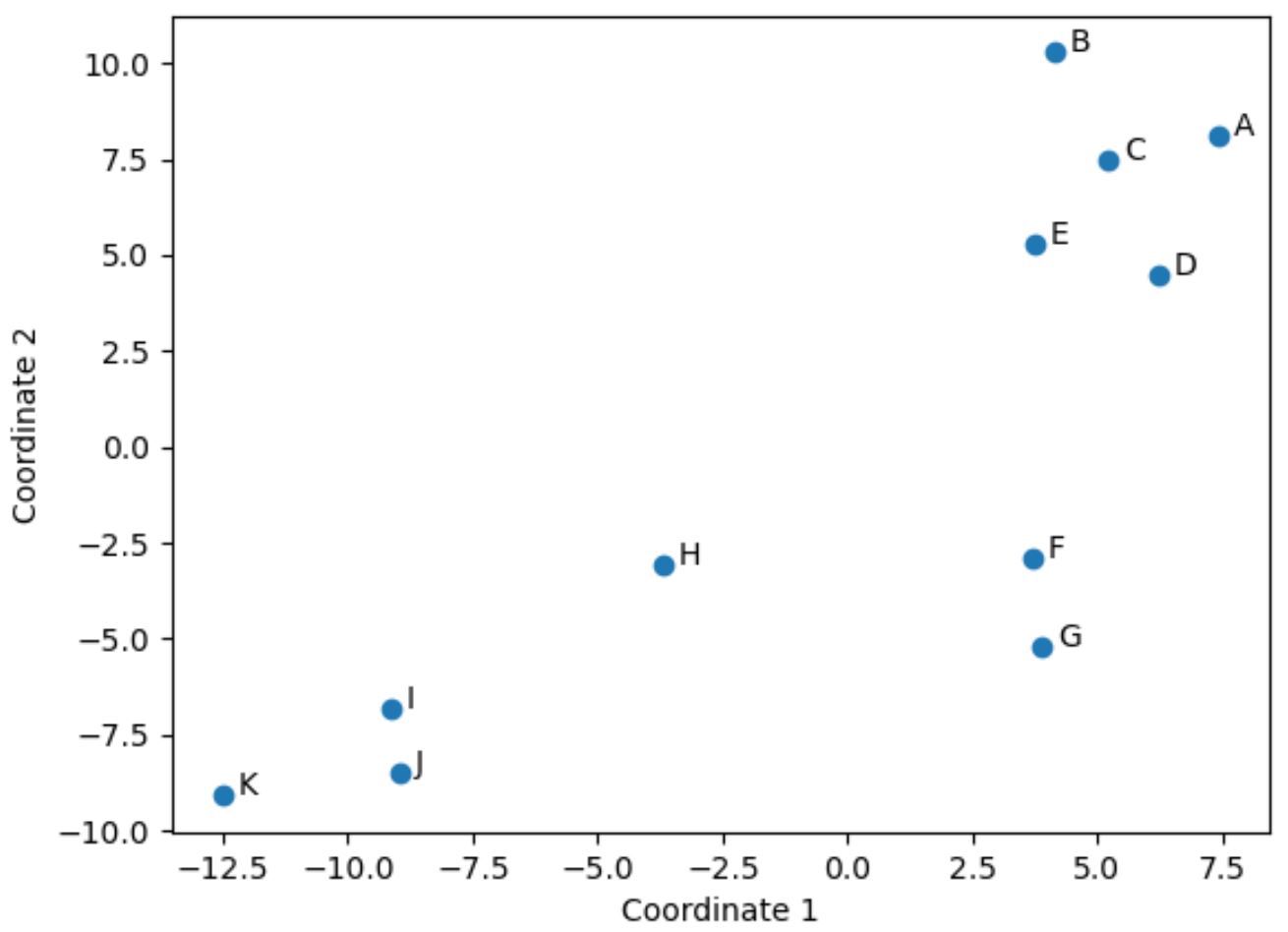
မူရင်းကော်လံလေးခုတွင် အလားတူတန်ဖိုးများရှိသည့် မူရင်း DataFrame ရှိ ကစားသမားများ (points, assists, blocks, and rebounds) များသည် ဇာတ်ကွက်ထဲတွင် တစ်ခုနှင့်တစ်ခု နီးကပ်နေပါသည်။

ဥပမာအားဖြင့်၊ ကစားသမား F နှင့် G သည် တစ်ခုနှင့်တစ်ခု ပိတ်ထားသည်။ ဤသည်မှာ မူရင်း DataFrame မှ ၎င်းတို့၏ တန်ဖိုးများဖြစ်သည်။

 #select rows with index labels 'F' and 'G'
df. loc [[' F ',' G ']]

        points assists blocks rebounds
player				
F 14 8 8 8
G 16 7 8 10

အမှတ်များ၊ အကူအညီများ၊ လုပ်ကွက်များနှင့် ပြန်လှန်ခြင်းများအတွက် ၎င်းတို့၏တန်ဖိုးများသည် 2D ဇာတ်ကွက်တွင် အဘယ်ကြောင့် အလွန်နီးကပ်နေကြသည်ကို ရှင်းပြသည်။

ဆန့်ကျင်ဘက်အနေနှင့်၊ ဇာတ်ကွက်ထဲတွင် ဝေးကွာနေသော ကစားသမား B နှင့် K ကို ထည့်သွင်းစဉ်းစားပါ။

မူရင်း DataFrame တွင် ၎င်းတို့၏တန်ဖိုးများကို ရည်ညွှန်းပါက၊ ၎င်းတို့သည် အလွန်ကွဲပြားသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်-

 #select rows with index labels 'B' and 'K'
df. loc [[' B ',' K ']]

        points assists blocks rebounds
player				
B 4 2 3 5
K 28 11 1 2

ထို့ကြောင့် 2D ဇာတ်ကွက်သည် DataFframe ရှိ ကိန်းရှင်အားလုံးတွင် ကစားသမားတစ်ဦးစီနှင့် မည်သို့ဆင်တူသည်ကို မြင်ယောင်ရန် ကောင်းမွန်သောနည်းလမ်းဖြစ်သည်။

တူညီသောကိန်းဂဏန်းများရှိသည့် ကစားသမားများကို ဇာတ်ကွက်ထဲတွင် ကွဲပြားသောကိန်းဂဏန်းများရှိသည့် ကစားသမားများသည် တစ်ဦးနှင့်တစ်ဦး ဝေးကွာနေချိန်တွင် အတူတကွ အုပ်စုဖွဲ့ထားသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ပါ သင်ခန်းစာများသည် Python တွင် အခြားသော အသုံးများသော အလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

Python တွင်ဒေတာကိုပုံမှန်ဖြစ်အောင်လုပ်နည်း
Python ရှိ Outliers ကိုမည်သို့ဖယ်ရှားနည်း
Python တွင် ပုံမှန်အခြေအနေအတွက် စမ်းသပ်နည်း