Python တွင် ရိုးရှင်းသော linear regression ကို မည်သို့လုပ်ဆောင်ရမည် (တစ်ဆင့်ပြီးတစ်ဆင့်)

Simple linear regression သည် single explanatory variable နှင့် single response variable အကြား ဆက်နွယ်မှုကို နားလည်ရန် ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည့် နည်းပညာတစ်ခုဖြစ်သည်။

ဤနည်းပညာသည် ဒေတာကို အကောင်းဆုံး “ အံဝင်ခွင်ကျ” သော မျဉ်းတစ်ကြောင်းကို ရှာဖွေပြီး အောက်ပါပုံစံကို ရယူသည်-

ŷ = b ₀ + b ₁ x

ရွှေ-

• ŷ : ခန့်မှန်းတုံ့ပြန်မှုတန်ဖိုး
• b ₀ : ဆုတ်ယုတ်မှုမျဉ်း၏ မူလအစ
• b ₁ : ဆုတ်ယုတ်မှုမျဉ်း၏ လျှောစောက်

ဤညီမျှခြင်းသည် ရှင်းလင်းချက်ကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်ကြားရှိ ဆက်နွယ်မှုကို နားလည်ရန် ကူညီပေးနိုင်ပြီး (၎င်းသည် ကိန်းဂဏန်းအရ သိသာထင်ရှားသည်ဟု ယူဆပါက) ၎င်းကို ရှင်းပြချက်ကိန်းရှင်၏တန်ဖိုးကို ပေးထားသည့် တုံ့ပြန်မှုကိန်းရှင်၏တန်ဖိုးကို ခန့်မှန်းရန် အသုံးပြုနိုင်သည်။

ဤသင်ခန်းစာသည် Python တွင် ရိုးရှင်းသော linear regression လုပ်ဆောင်နည်းကို အဆင့်ဆင့် ရှင်းလင်းချက်ပေးပါသည်။

အဆင့် 1: ဒေတာကို တင်ပါ။

ဤဥပမာအတွက်၊ ကျွန်ုပ်တို့သည် ကျောင်းသား 15 ဦးအတွက် အောက်ပါကိန်းရှင်နှစ်ခုပါရှိသော ဒေတာအတွဲအတုကို ဖန်တီးပါမည်။

• အချို့သော စာမေးပွဲများအတွက် စုစုပေါင်း လေ့လာသည့် နာရီများ
• စာမေးပွဲရလဒ်

ရှင်းပြချက်ကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် စာမေးပွဲရလဒ်များ အဖြစ် နာရီများကို အသုံးပြု၍ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံကို အံဝင်ခွင်ကျဖြစ်အောင် ကျွန်ုပ်တို့ကြိုးပမ်းပါမည်။

အောက်ပါကုဒ်သည် Python တွင် ဤဒေတာအတွဲအတုကို ဖန်တီးနည်းကို ပြသသည်-

 import pandas as pd

#create dataset
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})
      

#view first six rows of dataset
df[0:6]

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81

အဆင့် 2- ဒေတာကို မြင်ယောင်ကြည့်ပါ။

ရိုးရှင်းသော linear regression model ကို မတပ်ဆင်မီ၊ ၎င်းကို နားလည်ရန် ဒေတာကို ဦးစွာ မြင်ယောင်ကြည့်ရပါမည်။

ပထမဦးစွာ၊ ကျွန်ုပ်တို့သည် နာရီ နှင့် ရမှတ်အကြား ဆက်စပ်မှုကို ခန့် မှန်းခြေအား ဖြင့် တစ်ပြေးညီဖြစ်နေကြောင်း သေချာစေလိုပါသည်။

ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်မှုကို မြင်ယောင်နိုင်ရန် ရိုးရှင်းသော အပိုင်းအစတစ်ခုကို ဖန်တီးနိုင်သည်-

 import matplotlib.pyplot as plt

plt. scatter (df.hours, df.score)
plt. title (' Hours studied vs. Exam Score ')
plt. xlabel (' Hours ')
plt. ylabel (' Score ')
plt. show ()

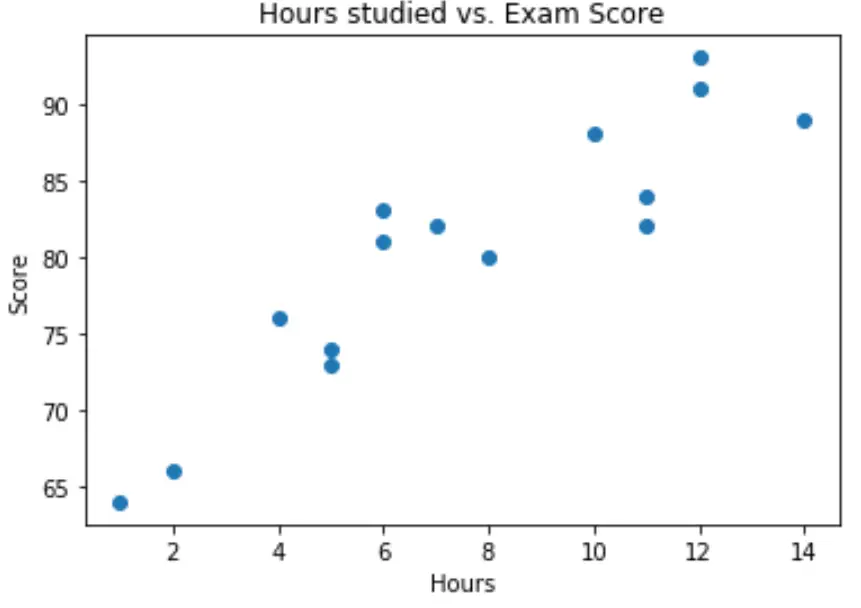
ဂရပ်မှ ဆက်စပ်မှုကို မျဉ်းသားပုံပေါ်ကြောင်း ကျွန်ုပ်တို့ မြင်နိုင်သည်။ နာရီအရေအတွက်များ လာသည်နှင့်အမျှ ရမှတ်သည်လည်း မျဉ်းဖြောင့်အတိုင်း တိုးလာပါသည်။

ထို့နောက် ကျွန်ုပ်တို့သည် စာမေးပွဲရလဒ်များ ဖြန့်ဝေမှုကို မြင်သာစေရန်နှင့် ကွာဟချက်များကို စစ်ဆေးရန် boxplot တစ်ခုကို ဖန်တီးနိုင်သည်။ ပုံသေအားဖြင့်၊ Python သည် တတိယ quartile (Q3) ထက် 1.5 ဆ သို့မဟုတ် ပထမ quartile (Q1) အောက်ရှိ interquartile အပိုင်းအခြား 1.5 ဆ သို့မဟုတ် 1.5 ဆ ရှိသော ကြားခံအကွာအဝေးကို အလွတ်သဘောအဖြစ် သတ်မှတ်သည်။

သတိပြုစရာတစ်ခုက ပိုသာလွန်ပါက၊ ကွက်လပ်တွင် စက်ဝိုင်းငယ်တစ်ခု ပေါ်လာပါမည်-

 df. boxplot (column=[' score ']) 

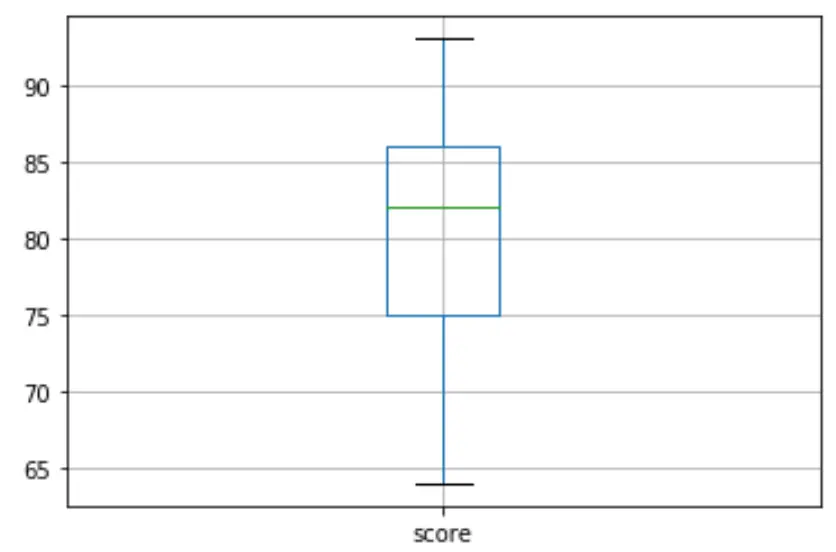
boxplot တွင် စက်ဝိုင်းငယ်များမရှိပါ၊ ဆိုလိုသည်မှာ ကျွန်ုပ်တို့၏ဒေတာအတွဲတွင် အစွန်းထွက်များမရှိပါ။

အဆင့် 3- ရိုးရှင်းသော Linear Regression ကိုလုပ်ဆောင်ပါ။

ကျွန်ုပ်တို့၏ variables များကြားက ဆက်နွယ်မှုမှာ linear ဖြစ်ပြီး outliers များ မရှိကြောင်း အတည်ပြုပြီးသည်နှင့်၊ ရှင်းပြချက် variable အဖြစ် နာရီများကို အသုံးပြု၍ ရိုးရှင်းသော linear regression model နှင့် တုံ့ပြန်မှု variable အဖြစ် ရမှတ်တို့ကို ဆက်လက်လုပ်ဆောင်နိုင်သည်-

မှတ်ချက်- ဆုတ်ယုတ်မှုပုံစံနှင့်ကိုက်ညီရန် statsmodels စာကြည့်တိုက်မှ OLS() လုပ်ဆောင်ချက်ကို အသုံးပြု ပါမည် ။

 import statsmodels.api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Mon, 26 Oct 2020 Prob (F-statistic): 2.25e-06
Time: 15:51:45 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

မော်ဒယ်အကျဉ်းချုပ်မှ၊ တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုညီမျှခြင်းမှာ-

ရမှတ် = 65.334 + 1.9824*(နာရီ)

ဆိုလိုသည်မှာ ထပ်လောင်းလေ့လာထားသော နာရီတိုင်းသည် ပျမ်းမျှ စာမေးပွဲရမှတ် 1.9824 မှတ် တိုးလာခြင်းနှင့် ဆက်စပ်နေသည်။ 65,334 ၏မူရင်းတန်ဖိုးသည် သုညနာရီစာလေ့လာနေသည့် ကျောင်းသားအတွက် ပျမ်းမျှမျှော်မှန်းထားသော စာမေးပွဲရမှတ်ကို ပြောပြသည်။

ကျောင်းသားတစ်ဦး၏လေ့လာမှုနာရီအရေအတွက်အပေါ်အခြေခံ၍မျှော်လင့်ထားသောစာမေးပွဲရမှတ်ကိုရှာဖွေရန်ဤညီမျှခြင်းကိုလည်းအသုံးပြုနိုင်သည်။ ဥပမာအားဖြင့်၊ 10 နာရီကြာလေ့လာသော ကျောင်းသားသည် စာမေးပွဲရမှတ် 85.158 ရရှိသင့်သည် ။

ရမှတ် = 65.334 + 1.9824*(10) = 85.158

ကျန်မော်ဒယ်အကျဉ်းချုပ်ကို ဤအရာက မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-

• P>|t| : ဤသည်မှာ မော်ဒယ် ဖော်ကိန်းများနှင့် ဆက်စပ်နေသည့် p-တန်ဖိုး ဖြစ်သည်။ နာရီ များအတွက် p-တန်ဖိုး (0.000) သည် 0.05 ထက် သိသိသာသာနည်းသောကြောင့်၊ နာရီ နှင့် ရမှတ်အကြား ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ဆက်စပ်မှုရှိသည်ဟု ကျွန်ုပ်တို့ပြောနိုင်သည်။
• R-squared- စာမေးပွဲရမှတ်များတွင် ကွဲလွဲမှုရာခိုင်နှုန်းကို လေ့လာသည့်နာရီအရေအတွက်ဖြင့် ရှင်းပြနိုင်သည်ဟု ဤနံပါတ်က ကျွန်ုပ်တို့အား ပြောပြသည်။ ယေဘူယျအားဖြင့်၊ regression model တစ်ခု၏ R-squared တန်ဖိုး ပိုကြီးလေ၊ explanatory variables များသည် response variable ၏ တန်ဖိုးကို ခန့်မှန်းနိုင်လေဖြစ်သည်။ ဤကိစ္စတွင်၊ ရမှတ်များကွဲလွဲမှု၏ 83.1% ကို နာရီများဖြင့် ရှင်းပြသည်။
• F-statistic နှင့် p-value- F-statistic ( 63.91 ) နှင့် သက်ဆိုင်ရာ p-value ( 2.25e-06 ) သည် ကျွန်ုပ်တို့အား ဆုတ်ယုတ်မှုပုံစံ၏ ယေဘုယျအဓိပ္ပာယ်ကို ပြောပြသည်၊ ဆိုလိုသည်မှာ မော်ဒယ်ရှိ ရှင်းပြထားသောကိန်းရှင်များသည် ကွဲလွဲမှုကို ရှင်းပြရာတွင် အသုံးဝင်သည်ရှိမရှိ၊ . တုံ့ပြန်မှု variable တွင်။ ဤဥပမာရှိ p-value သည် 0.05 ထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့၏မော်ဒယ်သည် စာရင်းအင်းအရ သိသာထင်ရှား ပြီး ရမှတ် ကွဲလွဲမှုကို ရှင်းပြရာတွင် အသုံးဝင်သည်ဟု ယူဆပါသည်။

အဆင့် 4- ကျန်ရှိသော မြေကွက်များကို ဖန်တီးပါ။

ရိုးရှင်းသော linear regression model ကို data နှင့် လိုက်လျောညီထွေဖြစ်စေပြီးနောက်၊ နောက်ဆုံးအဆင့်မှာ ကျန်ရှိသောကွက်များကို ဖန်တီးရန်ဖြစ်သည်။

linear regression ၏ အဓိက ယူဆချက် တစ်ခုမှာ regression model တစ်ခု၏ အကြွင်းအကျန်များသည် ခန့်မှန်းခြေအားဖြင့် ပုံမှန်အတိုင်း ဖြန့်ဝေထားပြီး ရှင်းပြနိုင်သော variable အဆင့်တစ်ခုစီတွင် homoscedastic ဖြစ်ကြပါသည်။ ဤယူဆချက်များနှင့် မကိုက်ညီပါက၊ ကျွန်ုပ်တို့၏ ဆုတ်ယုတ်မှုပုံစံ၏ ရလဒ်များသည် လွဲမှားနိုင်သည် သို့မဟုတ် ယုံကြည်စိတ်ချရခြင်းမရှိပေ။

ဤယူဆချက်များနှင့် ကိုက်ညီကြောင်း အတည်ပြုရန်၊ အောက်ဖော်ပြပါ အကြွင်းအကျန်များကို ကျွန်ုပ်တို့ ဖန်တီးနိုင်သည်-

အကြွင်းအကျန်များ၏ ကွက်ကွက်များနှင့် တပ်ဆင်ထားသော တန်ဖိုးများ- ဤကွက်ကွက်သည် မျိုးတူရိုးကျဖြစ်ခြင်းကို အတည်ပြုရန်အတွက် အသုံးဝင်သည်။ x-axis သည် တပ်ဆင်ထားသောတန်ဖိုးများကိုပြသပြီး y-axis သည် အကြွင်းအကျန်များကိုပြသသည်။ အကြွင်းအကျန်များသည် သုညတန်ဖိုးဝန်းကျင်ရှိ ဂရပ်တစ်လျှောက်လုံး ကျပန်းနှင့် တစ်ပြေးညီ ဖြန့်ဝေနေသရွေ့၊ မျိုးတူရိုးကျဖြစ်ခြင်းကို ချိုးဖောက်ခြင်းမဟုတ်ဟု ကျွန်ုပ်တို့ ယူဆနိုင်သည်-

 #define figure size
fig = plt. figure (figsize=(12.8))

#produce residual plots
fig = sm.graphics. plot_regress_exog (model, ' hours ', fig=fig)

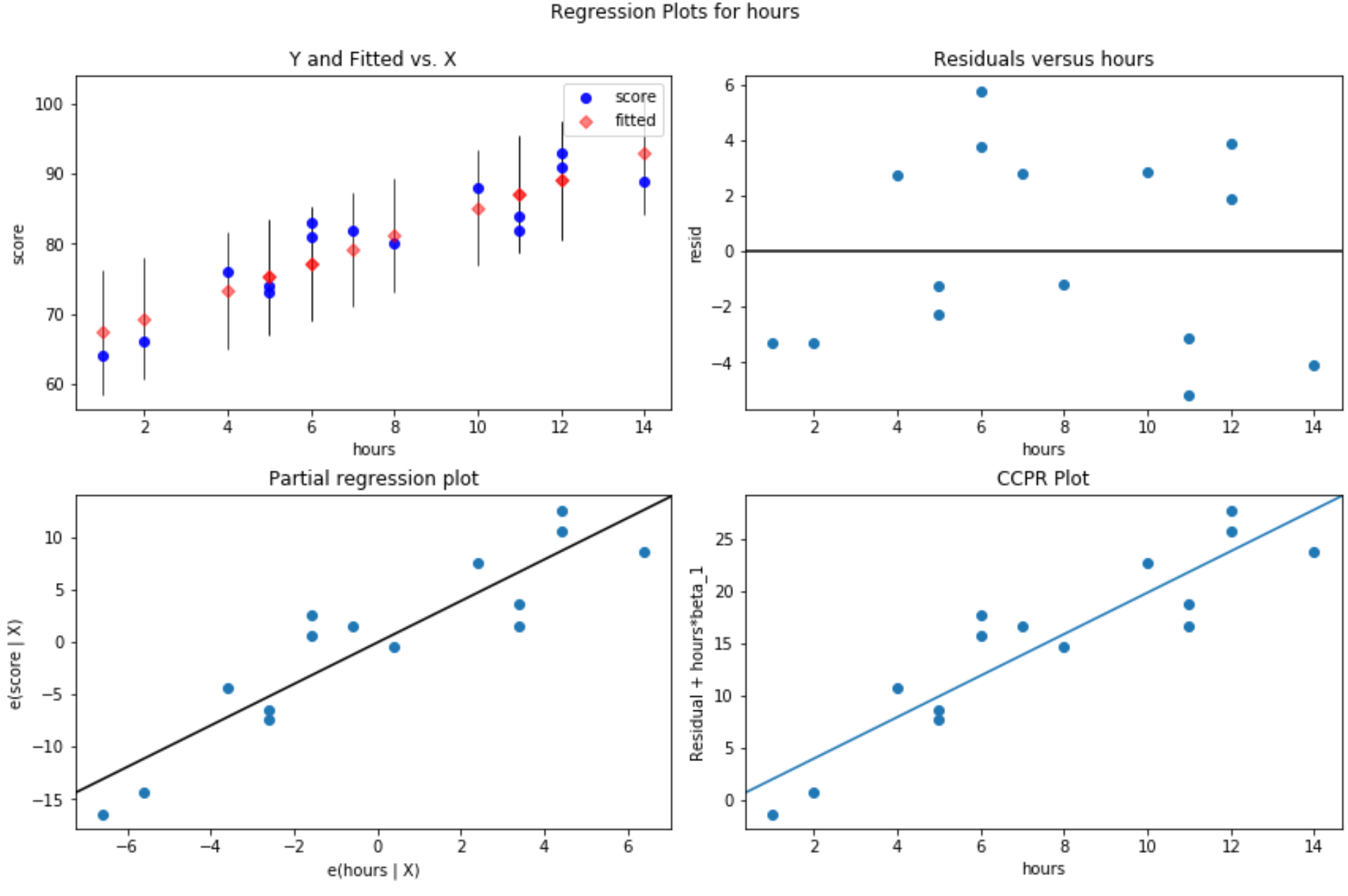
မြေကွက် လေးကွက် ထုတ်လုပ်သည်။ ညာဘက်အပေါ်ထောင့်ရှိ ကွက်ကွက်သည် ချိန်ညှိထားသော ကွက်လပ်နှင့် ကျန်ရှိသော ကွက်ကွက်ဖြစ်သည်။ ဤကွက်လပ်ရှိ x-axis သည် ခန့်မှန်းသူ variable point များ၏ တကယ့်တန်ဖိုးများကို ပြသပြီး y-axis သည် ထိုတန်ဖိုးအတွက် ကျန်ရှိသောတန်ဖိုးများကို ပြသသည်။

အကြွင်းအကျန်များသည် သုညဝန်းကျင်တွင် ကျပန်းကျပန်း ပြန့်ကျဲနေပုံပေါ်သောကြောင့်၊ ၎င်းသည် မျိုးကွဲကွဲပြားမှုသည် ရှင်းပြနိုင်သောကိန်းရှင်အတွက် ပြဿနာမဟုတ်ကြောင်း ညွှန်ပြသည်။

QQ ကွက်- ဤကွက်ကွက်သည် အကြွင်းအကျန်များသည် ပုံမှန်ဖြန့်ဝေမှုနောက်သို့ လိုက်ခြင်းရှိမရှိ ဆုံးဖြတ်ရန်အတွက် အသုံးဝင်သည်။ ကွက်လပ်ရှိ ဒေတာတန်ဖိုးများသည် 45 ဒီဂရီထောင့်တွင် အကြမ်းဖျင်းဖြောင့်မျဉ်းအတိုင်း လိုက်နာပါက၊ ဒေတာကို ပုံမှန်အားဖြင့် ဖြန့်ဝေသည်-

 #define residuals
res = model. reside

#create QQ plot
fig = sm. qqplot (res, fit= True , line=" 45 ")
plt.show() 

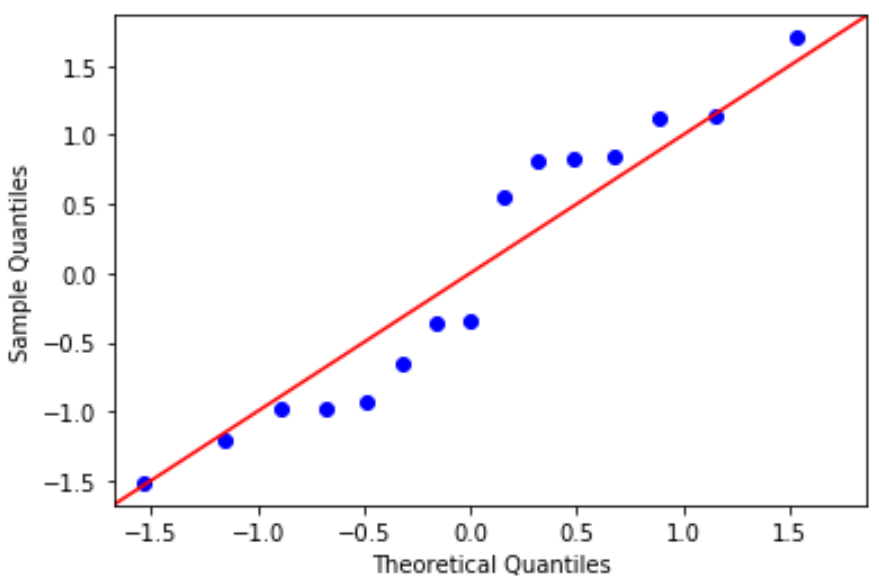
အကြွင်းအကျန်များသည် 45 ဒီဂရီမျဉ်းမှ အနည်းငယ်သွေဖည်သွားသော်လည်း ပြင်းထန်သောစိုးရိမ်မှုဖြစ်စေရန် မလုံလောက်ပါ။ ပုံမှန်ဖြစ်ရိုးဖြစ်စဉ် ယူဆချက်နှင့် ကိုက်ညီသည်ဟု ကျွန်ုပ်တို့ ယူဆနိုင်သည်။

အကြွင်းအကျန်များကို ပုံမှန်အတိုင်း ဖြန့်ဝေပြီး homoscedastic ဖြစ်သောကြောင့်၊ ရိုးရှင်းသော မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုပုံစံ၏ ယူဆချက်များနှင့် ကိုက်ညီကြောင်း စစ်ဆေးတွေ့ရှိပါသည်။ ထို့ကြောင့် ကျွန်ုပ်တို့၏ မော်ဒယ်၏ထွက်ရှိမှုသည် ယုံကြည်စိတ်ချရသည်။

ဤသင်ခန်းစာတွင်အသုံးပြုထားသော Python ကုဒ်အပြည့်အစုံကို ဤနေရာတွင် တွေ့နိုင်ပါသည်။