Python တွင် residual plot ဖန်တီးနည်း

ကျန်ရှိသောကွက်ကွက် သည် ဆုတ်ယုတ်မှုပုံစံ ၏ အကြွင်းများနှင့် ကိုက်ညီသောတန်ဖိုးများကို ပြသသည့်ကွက်ကွက်အမျိုးအစားတစ်ခုဖြစ်သည်။

ဤကွက်ကွက်အမျိုးအစားသည် ပေးထားသောဒေတာအစုံအတွက် သင့်လျော်မှုရှိမရှိ အကဲဖြတ်ရန်နှင့် အကြွင်း အ ကျန်များကို စစ်ဆေးရန်အတွက် အသုံးပြုလေ့ရှိသည်။

ဤသင်ခန်းစာတွင် Python ရှိ မျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံအတွက် ကျန်နေသောကွက်ကွက်တစ်ခုကို ဖန်တီးနည်းကို ရှင်းပြထားသည်။

ဥပမာ- Python တွင် ကျန်ရှိသောကွက်ကွက်

ဤဥပမာအတွက်၊ ကျွန်ုပ်တို့သည် ဘတ်စကတ်ဘောကစားသမား 10 ဦး၏ အရည်အချင်းများကို ဖော်ပြသည့် ဒေတာအတွဲကို အသုံးပြုပါမည်-

 import numpy as np
import pandas as pd

#create dataset
df = pd.DataFrame({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19],
                   'assists': [5, 7, 7, 8, 5, 7, 6, 9, 9, 5],
                   'rebounds': [11, 8, 10, 6, 6, 9, 6, 10, 10, 7]})

#view dataset
df

	rating points assists rebounds
0 90 25 5 11
1 85 20 7 8
2 82 14 7 10
3 88 16 8 6
4 94 27 5 6
5 90 20 7 9
6 76 12 6 6
7 75 15 9 10
8 87 14 9 10
9 86 19 5 7

ရိုးရှင်းသော မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းအတွက် အကြွင်းအကျန်ကွက်

ကျွန်ုပ်တို့သည် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် ခန့်မှန်းကိန်းရှင်ကိန်းရှင်နှင့် အဆင့် အဖြစ် အမှတ်များကို အသုံးပြုကာ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံကို အံကိုက်ဆိုပါစို့။

 #import necessary libraries
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols

#fit simple linear regression model
model = ols('rating ~ points', data=df). fit ()

#view model summary
print(model.summary())

ကျွန်ုပ်တို့သည် statsmodels စာကြည့်တိုက်မှ plot_regress_exog() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ ကျန်ရှိသော သို့မဟုတ် တပ်ဆင်ထားသော ကွက်ကွက်တစ်ခုကို ဖန်တီးနိုင်သည်-

 #define figure size
fig = plt.figure(figsize=(12,8))

#produce regression plots
fig = sm.graphics.plot_regress_exog(model, ' points ', fig=fig)

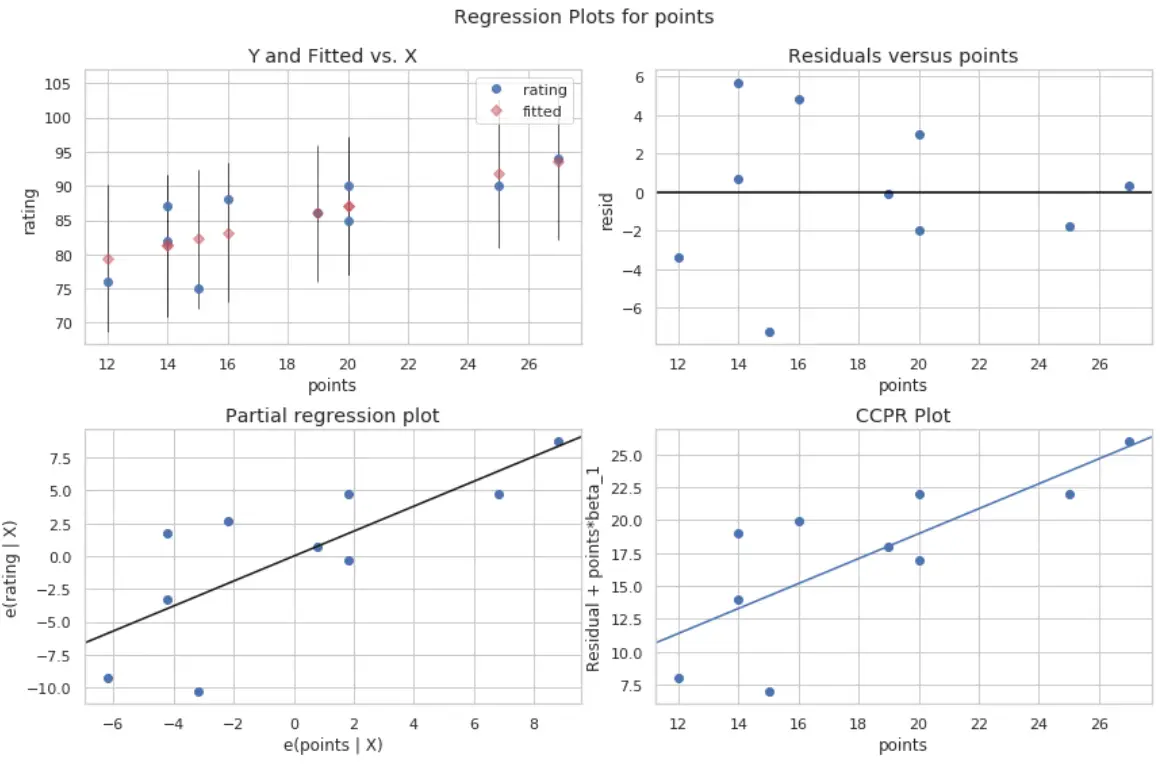
မြေကွက် လေးကွက် ထုတ်လုပ်သည်။ ညာဘက်အပေါ်ထောင့်ရှိ ကွက်ကွက်သည် ချိန်ညှိထားသော ကွက်လပ်နှင့် ကျန်ရှိသော ကွက်ကွက်ဖြစ်သည်။ ဤကွက်လပ်ရှိ x-axis သည် ခန့်မှန်းသူ variable point များ၏ တကယ့်တန်ဖိုးများကို ပြသပြီး y-axis သည် ထိုတန်ဖိုးအတွက် ကျန်ရှိသောတန်ဖိုးများကို ပြသသည်။

အကြွင်းအကျန်များသည် သုညဝန်းကျင်တွင် ကျပန်းကျပန်း ပြန့်ကျဲနေပုံပေါ်သောကြောင့်၊ ၎င်းသည် ကြိုတင်တွက်ဆထားသောကိန်းရှင်အတွက် ပြဿနာမဟုတ်ကြောင်း ဖော်ပြသည်။

မျဉ်းကြောင်း ဆုတ်ယုတ်မှု အများအပြားအတွက် အကြွင်းအကျန်ကွက်များ

ကြိုတင်ခန့်မှန်းကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် အဆင့်သတ်မှတ်ခြင်း အဖြစ် assists နှင့် rebounds ကို အသုံးပြု၍ များစွာသော linear regression မော်ဒယ်ကို ကျွန်ုပ်တို့ အံဝင်ခွင်ကျဆိုပါစို့။

 #fit multiple linear regression model
model = ols('rating ~ assists + rebounds', data=df). fit ()

#view model summary
print(model.summary())

တစ်ဖန်၊ ကျွန်ုပ်တို့သည် statsmodels ဒစ်ဂျစ်တိုက်မှ plot_regress_exog() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ တစ်ဦးချင်းစီ ကြိုတင်ခန့်မှန်းသူတိုင်းအတွက် ကျန်ရှိသော ဆန့်ကျင်မှု ခန့်မှန်းကွက်တစ်ခုကို ဖန်တီးနိုင်သည်။

ဥပမာအားဖြင့်၊ ဤအရာသည် ခန့်မှန်းသူ variable assists အတွက် ကျန်ရှိသော/predictor plot နှင့်တူသည်-

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' assists ', fig=fig)

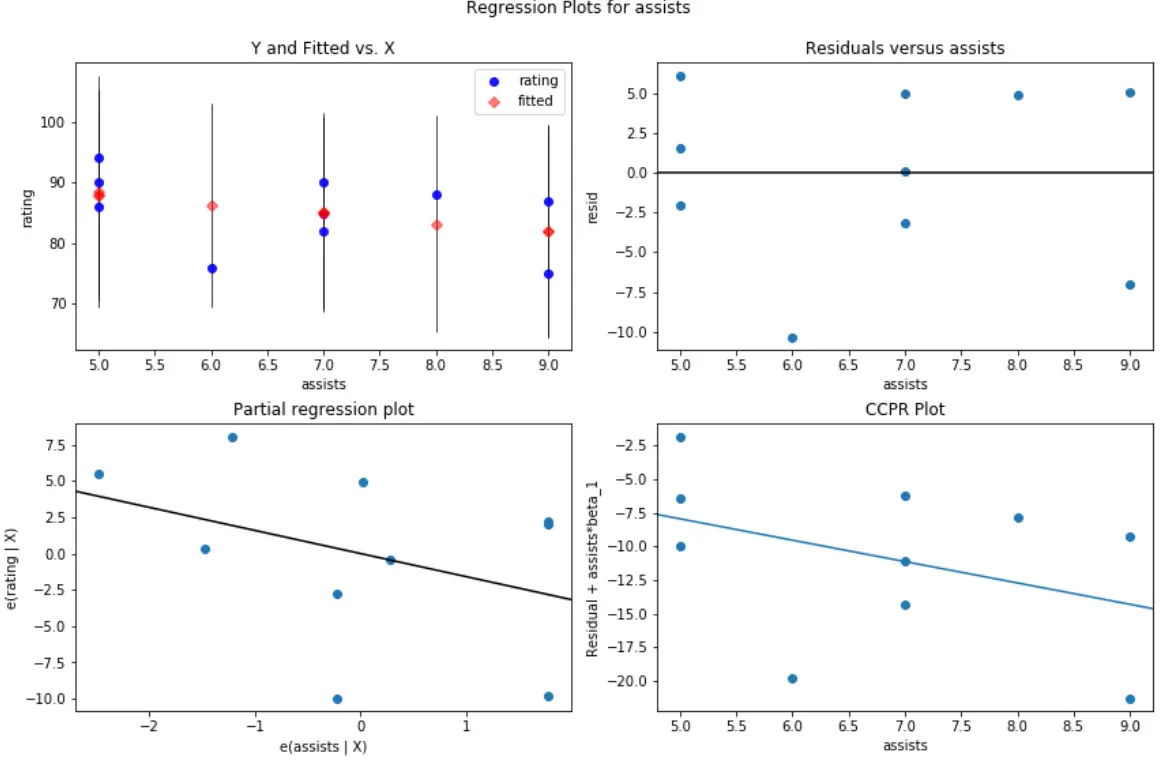
ဤအရာသည် ခန့်မှန်းသူကိန်းရှင်၏ ပြန်ထွက်ခြင်း အတွက် ကျန်ရှိ/ခန့်မှန်းသူ၏ ကွက်ကွက်ပုံသဏ္ဌာန်ဖြစ်သည်။

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' rebounds ', fig=fig)

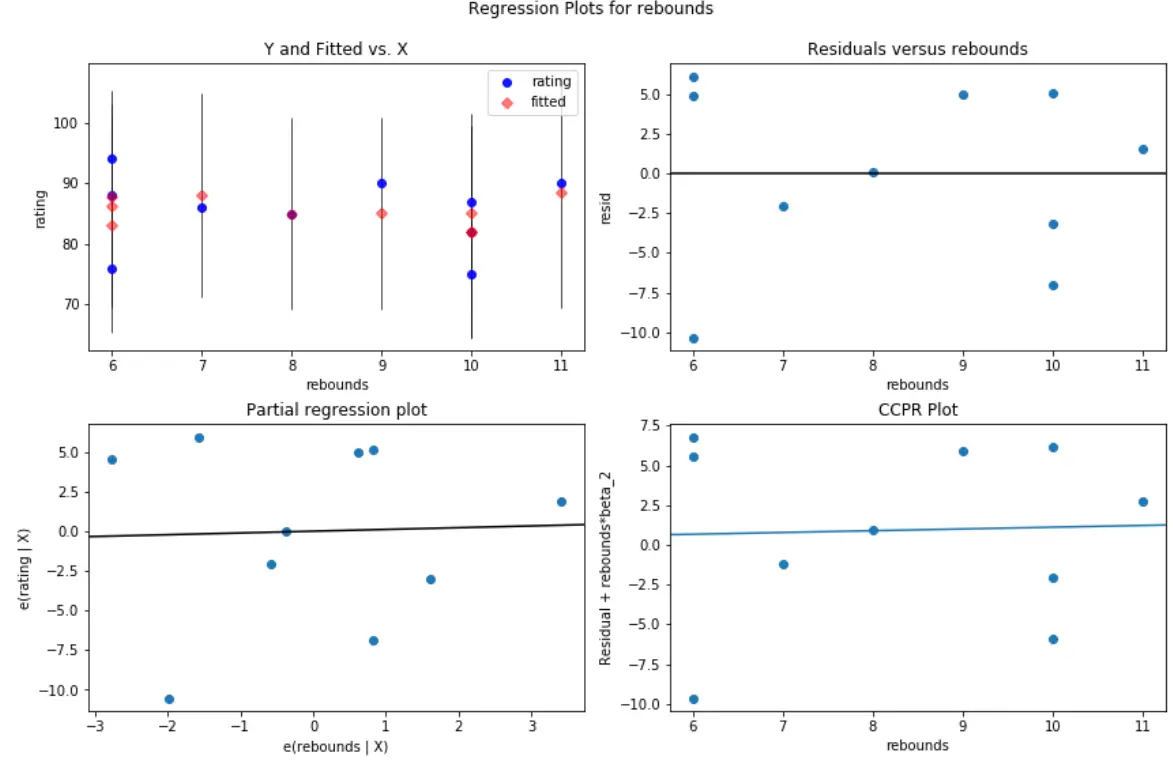
ကွက်နှစ်ခုစလုံးတွင်၊ ကျန်အကြွင်းအကျန်များသည် သုညဝန်းကျင်တွင် ကျပန်းကျပန်း ပြန့်ကျဲနေပုံရပြီး heteroskedasticity သည် မော်ဒယ်ရှိ ကြိုတင်ခန့်မှန်းကိန်းရှင်များအတွက် ပြဿနာမဟုတ်ကြောင်း ညွှန်ပြသည်။