Python တွင် quadratic regression လုပ်ဆောင်နည်း

Quadratic regression သည် ဂရပ်တစ်ခုပေါ်ရှိ “ U” သို့မဟုတ် ပြောင်းပြန် “ U” ကဲ့သို့ဖြစ်နိုင်သည်ဟူသော ဆက်စပ်မှုအစစ်အမှန်များသည် လေးထောင့်ပုံသဏ္ဍာန်ဖြစ်သည့်အခါ ကြိုတင်ခန့်မှန်းကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်ကြားဆက်ဆံရေးကို တွက်ချက်ရန် ကျွန်ုပ်တို့အသုံးပြုနိုင်သော ဆုတ်ယုတ်မှုအမျိုးအစားတစ်ခုဖြစ်သည်။

ဆိုလိုသည်မှာ ခန့်မှန်းသူကိန်းရှင် တိုးလာသည်နှင့်အမျှ၊ တုံ့ပြန်မှုကိန်းရှင်သည် တိုးလာတတ်သည်၊ သို့သော် ခန့်မှန်းချက်ကိန်းရှင်သည် ဆက်လက်တိုးလာသောကြောင့် တုံ့ပြန်မှုကိန်းရှင်သည် ကျဆင်းသွားပါသည်။

ဤသင်ခန်းစာတွင် Python တွင် လေးပုံတပုံ ဆုတ်ယုတ်မှုအား မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

ဥပမာ- Python ရှိ Quadratic Regression

ကျွန်ုပ်တို့တွင် တစ်ပတ်လျှင် အလုပ်လုပ်သော နာရီအရေအတွက်နှင့် ပတ်သက်သော ဒေတာရှိပြီး လူ 16 ဦးအတွက် ပျော်ရွှင်မှုအဆင့် (0 မှ 100 အထိ) အစီရင်ခံသည်ဆိုပါစို့။

 import numpy as np
import scipy.stats as stats

#define variables
hours = [6, 9, 12, 12, 15, 21, 24, 24, 27, 30, 36, 39, 45, 48, 57, 60]
happ = [12, 18, 30, 42, 48, 78, 90, 96, 96, 90, 84, 78, 66, 54, 36, 24]

ဤဒေတာ၏ ရိုးရှင်းသော ခွဲခြမ်းစိတ်ဖြာမှုကို ကျွန်ုပ်တို့ပြုလုပ်ပါက၊ ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်နွယ်မှုမှာ “ U” ပုံသဏ္ဍာန်ဖြစ်သည်-

 import matplotlib.pyplot as plt

#create scatterplot
plt.scatter(hours, happ) 

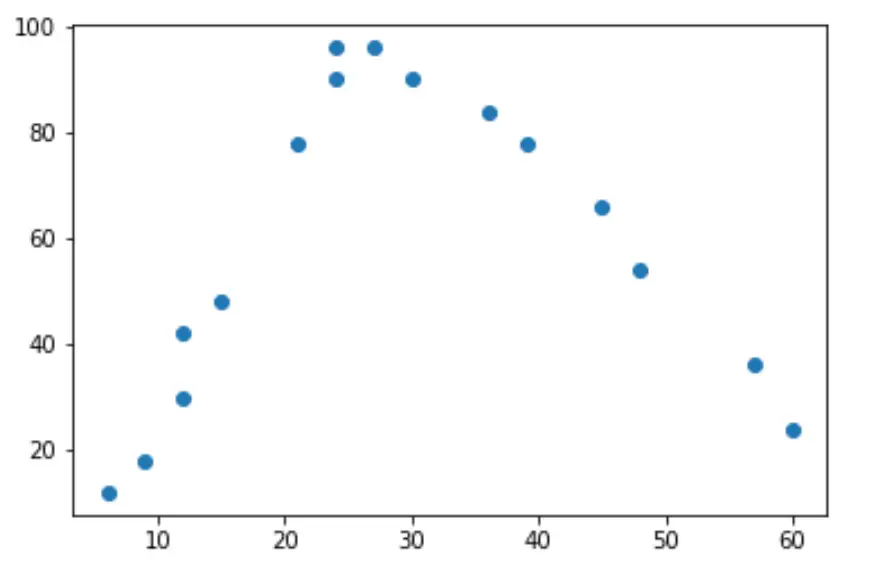
အလုပ်ချိန်များလာသည်နှင့်အမျှ ပျော်ရွှင်မှုလည်း တိုးလာသော်လည်း တစ်ပတ်လျှင် အလုပ်ချိန် ၃၅ နာရီထက်ကျော်လွန်လာသည်နှင့်အမျှ ပျော်ရွှင်မှု လျော့နည်းလာသည်။

ဤ “ U” ပုံသဏ္ဍာန်ကြောင့်၊ ဆိုလိုသည်မှာ လေးပုံတပုံ ဆုတ်ယုတ်မှုသည် ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်နွယ်မှုကို တွက်ချက်ရန်အတွက် ကောင်းမွန်သော ကိုယ်စားလှယ်လောင်း ဖြစ်နိုင်သည်ဟု ဆိုလိုသည်။

quadratic regression ကို အမှန်တကယ်လုပ်ဆောင်ရန်၊ numpy.polyfit() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ ဒီဂရီ 2 ရှိသည့် ပေါလီနိုမီးယား ဆုတ်ယုတ်မှုပုံစံကို ကျွန်ုပ်တို့ တပ်ဆင်နိုင်သည် ။

 import numpy as np

#polynomial fit with degree = 2
model = np.poly1d(np.polyfit(hours, happ, 2))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 60, 50)
plt.scatter(hours, happ)
plt.plot(polyline, model(polyline))
plt.show() 

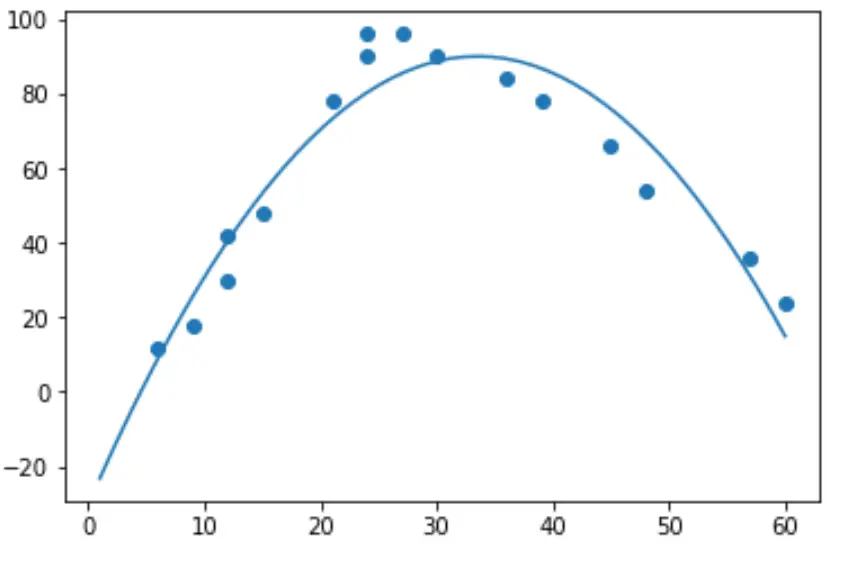
မော်ဒယ် coefficients ကို ရိုက်နှိပ်ခြင်းဖြင့် တပ်ဆင်ထားသော polynomial regression equation ကို ရယူနိုင်ပါသည်။

 print (model)

-0.107x 2 + 7.173x - 30.25

တပ်ဆင်ထားသော လေးထောင့်ကိန်းဂဏန်း ဆုတ်ယုတ်မှုညီမျှခြင်းမှာ-

ပျော်ရွှင်မှု = -0.107(နာရီ) ² + 7.173(နာရီ) – 30.25

အလုပ်ချိန်ပေါ်မူတည်၍ လူတစ်ဦးချင်းစီ၏ မျှော်လင့်ထားသော ပျော်ရွှင်မှုအဆင့်ကို တွက်ချက်ရန် ဤညီမျှခြင်းအား ကျွန်ုပ်တို့အသုံးပြုနိုင်ပါသည်။ ဥပမာအားဖြင့်၊ တစ်ပတ်လျှင် နာရီ 30 အလုပ်လုပ်သူ၏ မျှော်လင့်ထားသော ပျော်ရွှင်မှုအဆင့်မှာ-

ပျော်ရွှင်မှု = -0.107(30) ² + 7.173(30) – 30.25 = 88.64 ။

မော်ဒယ်၏ R-squared ကိုရရန် အတိုချုံးရေးနိုင်သည်၊ ၎င်းသည် ခန့်မှန်းသူကိန်းရှင်များဖြင့် ရှင်းပြနိုင်သော တုံ့ပြန်မှုကိန်းရှင်ရှိ ကွဲလွဲမှု၏အချိုးအစားဖြစ်သည်။

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np.polyfit(x, y, degree)
    p = np.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat-ybar)**2)
    sstot = np.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(hours, happ, 2)

{'r_squared': 0.9092114182131691}

ဤဥပမာတွင်၊ မော်ဒယ်၏ R စတုရန်းသည် 0.9092 ဖြစ်သည်။

ဆိုလိုသည်မှာ အစီရင်ခံထားသော ပျော်ရွှင်မှုအဆင့်များတွင် ကွဲလွဲမှု 90.92% ကို ခန့်မှန်းသူကိန်းရှင်များဖြင့် ရှင်းပြနိုင်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

Python တွင် polynomial regression လုပ်နည်း
R တွင် quadratic regression ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
Excel တွင် လေးပုံတပုံ ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်နည်း