R in ridge regression (တစ်ဆင့်ပြီးတစ်ဆင့်)

Ridge regression သည် data တွင် multicollinearity ရှိနေသောအခါတွင် regression model တစ်ခုနှင့်ကိုက်ညီရန်ကျွန်ုပ်တို့အသုံးပြုနိုင်သောနည်းလမ်းတစ်ခုဖြစ်သည်။

အတိုချုပ်အားဖြင့်၊ အနည်း ဆုံး စတုရန်းဆုတ်ယုတ်မှု သည် ကျန်ရှိသော စတုရန်း ပေါင်းလဒ် (RSS) ကို အနည်းဆုံး လျှော့ချနိုင်သော ကိန်းကိန်း ခန့်မှန်းချက်များကို ရှာဖွေရန် ကြိုးပမ်းသည် ။

RSS = Σ(y _i – ŷ _i )၂

ရွှေ-

• ∑ : ပေါင်းလဒ် ဟု အဓိပ္ပာယ်ရသော ဂရိသင်္ကေတ
• y _i : ^{အိုင်တီ} လေ့လာခြင်းအတွက် အမှန်တကယ် တုံ့ပြန်မှုတန်ဖိုး
• ŷ _i : Multiple linear regression model ကို အခြေခံ၍ ခန့်မှန်းထားသော တုံ့ပြန်မှုတန်ဖိုး

အပြန်အလှန်အားဖြင့်၊ တောင်ကြောဆုတ်ယုတ်မှုသည် အောက်ပါတို့ကို လျှော့ချရန် ကြိုးပမ်းသည်-

RSS + λΣβ _j ^၂

j သည် 1 မှ p ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် λ ≥ 0 ရှိရာသို့ သွားပါသည်။

ညီမျှခြင်းတွင် ဤဒုတိယအခေါ်အဝေါ်ကို ရုပ်သိမ်းပြစ်ဒဏ် ဟု ခေါ်သည်။ အခေါင်ဆုတ်ယုတ်မှုတွင်၊ ဖြစ်နိုင်ခြေအနည်းဆုံး MSE စမ်းသပ်မှု (ပျမ်းမျှစတုရန်းအမှား) ကိုထုတ်ပေးသည့် λ တန်ဖိုးတစ်ခုကို ကျွန်ုပ်တို့ရွေးချယ်သည်။

ဤကျူတိုရီရယ်တွင် R တွင် ကုန်းပတ်ဆုတ်ယုတ်မှုလုပ်ဆောင်ပုံအဆင့်ဆင့်ကို ဥပမာပေးထားသည်။

အဆင့် 1: ဒေတာကို တင်ပါ။

ဤဥပမာအတွက်၊ ကျွန်ုပ်တို့သည် mtcars ဟုခေါ်သော R ၏ built-in ဒေတာအတွဲကို အသုံးပြုပါမည်။ ကျွန်ုပ်တို့သည် တုံ့ပြန်မှု variable အဖြစ် hp ကို အသုံးပြုပြီး အောက်ပါ variable များကို ကြိုတင်ခန့်မှန်းသူများအဖြစ် အသုံးပြုပါမည်။

• စိုင်းစိုင်းခမ်းလှိုင်
• ကိုယ်အလေးချိန်
• ပြောရမှာပါ။
• qsec

တောင်ကြောဆုတ်ယုတ်မှုလုပ်ဆောင်ရန်၊ ကျွန်ုပ်တို့သည် glmnet ပက်ကေ့ခ်ျမှ လုပ်ဆောင်ချက်များကို အသုံးပြုပါမည်။ ဤပက်ကေ့ဂျ်တွင် တုံ့ပြန်မှုကိန်းရှင်သည် vector ဖြစ်ရန်နှင့် ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်အစုအစုသည် data.matrix အတန်းအစားဖြစ်ရန် လိုအပ်သည်။

အောက်ဖော်ပြပါ ကုဒ်သည် ကျွန်ုပ်တို့၏ဒေတာကို သတ်မှတ်ပုံဖော်ပြသည်-

 #define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

အဆင့် 2- Ridge Regression Model ကို အံကိုက်လုပ်ပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် Ridge regression မော်ဒယ်နှင့် ကိုက်ညီရန် glmnet() လုပ်ဆောင်ချက်ကို အသုံးပြုပြီး alpha=0 ကို သတ်မှတ်ပေးပါမည်။

1 နှင့် ညီမျှသော အယ်လ်ဖာသတ်မှတ်ခြင်းသည် Lasso ဆုတ်ယုတ်မှုကို အသုံးပြုခြင်းနှင့် ညီမျှပြီး 0 နှင့် 1 ကြားတန်ဖိုးသို့ အယ်လ်ဖာသတ်မှတ်ခြင်းသည် elastic ပိုက်ကို အသုံးပြုခြင်းနှင့် ညီမျှကြောင်း သတိပြုပါ။

ခေါင်ဆုတ်ယုတ်မှုသည် ကိန်းရှင်တစ်ခုစီတွင် 0 နှင့် စံသွေဖည်မှု 1 ရှိသည်ဟူသော ခန့်မှန်းချက်ကိန်းရှင်တစ်ခုစီတွင် စံချိန်စံညွှန်းသတ်မှတ်ရန် အချက်အလက် လိုအပ်ကြောင်းကိုလည်း သတိပြုပါ။

ကံကောင်းထောက်မစွာ၊ glmnet() သည် သင့်အတွက် ဤစံသတ်မှတ်ချက်ကို အလိုအလျောက် လုပ်ဆောင်ပေးပါသည်။ အကယ်၍ သင်သည် ကိန်းရှင်များကို စံသတ်မှတ်ထားပြီးဖြစ်ပါက၊ သင်သည် standardize=False ကို သတ်မှတ်နိုင်သည်။

 library (glmnet)

#fit ridge regression model
model <- glmnet(x, y, alpha = 0 )

#view summary of model
summary(model)

          Length Class Mode   
a0 100 -none- numeric
beta 400 dgCMatrix S4     
df 100 -none- numeric
dim 2 -none- numeric
lambda 100 -none- numeric
dev.ratio 100 -none- numeric
nulldev 1 -none- numeric
npasses 1 -none- numeric
jerr 1 -none- numeric
offset 1 -none- logical
call 4 -none- call   
nobs 1 -none- numeric

အဆင့် 3- Lambda အတွက် အကောင်းဆုံးတန်ဖိုးကို ရွေးပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် k-fold cross-validation ကို အသုံးပြု၍ အနိမ့်ဆုံးစမ်းသပ်မှုပျမ်းမျှနှစ်ထပ်အမှား (MSE) ကိုထုတ်ပေးသည့် lambda တန်ဖိုးကို ဖော်ထုတ်ပါမည်။

ကံကောင်းထောက်မစွာ၊ glmnet တွင် k = 10 ကြိမ်အသုံးပြု၍ k-fold cross-validation အလိုအလျောက်လုပ်ဆောင်ပေးသည့် cv.glmnet() လုပ်ဆောင်ချက်ရှိသည်။

 #perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 0 )

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda

[1] 10.04567

#produce plot of test MSE by lambda value
plot(cv_model) 

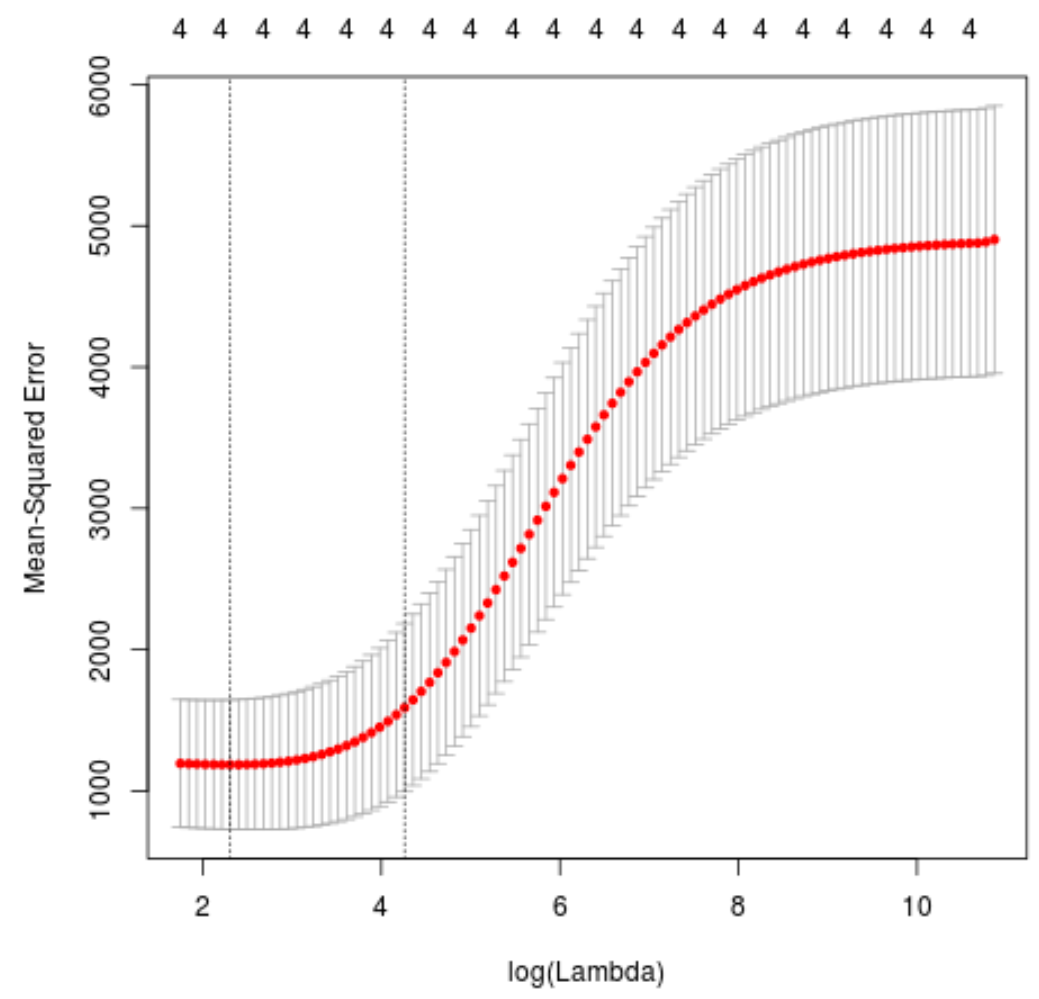
MSE စမ်းသပ်မှုကို လျှော့ချပေးသည့် lambda တန်ဖိုးသည် 10.04567 ဖြစ်သွားသည်။

အဆင့် 4- နောက်ဆုံးပုံစံကို ပိုင်းခြားစိတ်ဖြာပါ။

နောက်ဆုံးတွင်၊ အကောင်းဆုံးသော lambda တန်ဖိုးဖြင့် ထုတ်လုပ်ထားသော နောက်ဆုံးမော်ဒယ်ကို ပိုင်းခြားစိတ်ဖြာနိုင်ပါသည်။

ဤမော်ဒယ်အတွက် ကိန်းဂဏန်း ခန့်မှန်းချက်များကို ရယူရန် အောက်ပါကုဒ်ကို အသုံးပြုနိုင်ပါသည်။

 #find coefficients of best model
best_model <- glmnet(x, y, alpha = 0 , lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                    s0
(Intercept) 475.242646
mpg -3.299732
wt 19.431238
drat -1.222429
qsec -17.949721

lambda တိုးလာခြင်းကြောင့် ကိန်းဂဏန်းခန့်မှန်းချက်များ မည်သို့ပြောင်းလဲသွားသည်ကို မြင်သာစေရန် Trace ကြံစည်မှုကိုလည်း ထုတ်လုပ်နိုင်သည်-

 #produce Ridge trace plot
plot(model, xvar = " lambda ") 

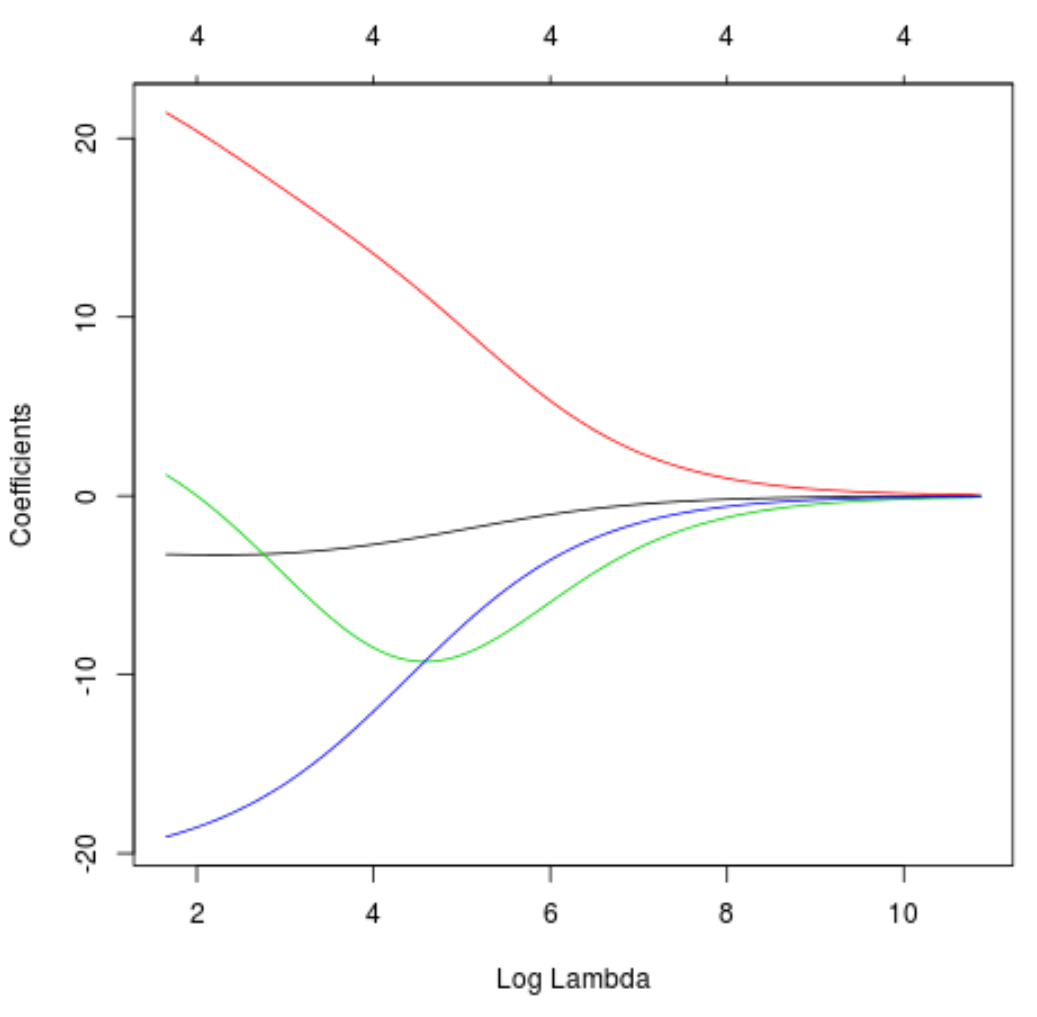
နောက်ဆုံးတွင်၊ သင်တန်းဒေတာတွင် မော်ဒယ်၏ R-squared ကို တွက်ချက်နိုင်သည်-

 #use fitted best model to make predictions
y_predicted <- predict (model, s = best_lambda, newx = x)

#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.7999513

R နှစ်ထပ်ကိန်းသည် 0.7999513 ဖြစ်သွားသည်။ ဆိုလိုသည်မှာ၊ အကောင်းဆုံးမော်ဒယ်သည် လေ့ကျင့်ရေးဒေတာ၏ တုံ့ပြန်မှုတန်ဖိုးများတွင် ကွဲလွဲမှု 79.99% ကို ရှင်းပြနိုင်ခဲ့သည်။

ဤဥပမာတွင်အသုံးပြုထားသော R ကုဒ်အပြည့်အစုံကို ဤနေရာတွင် ရှာတွေ့နိုင်ပါသည်။