R in lasso regression (တစ်ဆင့်ပြီးတစ်ဆင့်)

Lasso regression သည် data တွင် multicollinearity ရှိနေသောအခါတွင် regression model တစ်ခုနှင့်ကိုက်ညီရန်ကျွန်ုပ်တို့အသုံးပြုနိုင်သောနည်းလမ်းတစ်ခုဖြစ်သည်။

အတိုချုပ်အားဖြင့်၊ အနည်း ဆုံး စတုရန်းဆုတ်ယုတ်မှု သည် ကျန်ရှိသော စတုရန်း ပေါင်းလဒ် (RSS) ကို အနည်းဆုံး လျှော့ချနိုင်သော ကိန်းကိန်း ခန့်မှန်းချက်များကို ရှာဖွေရန် ကြိုးပမ်းသည် ။

RSS = Σ(y _i – ŷ _i )၂

ရွှေ-

• ∑ : ပေါင်းလဒ် ဟု အဓိပ္ပာယ်ရသော ဂရိသင်္ကေတ
• y _i : ^{အိုင်တီ} လေ့လာခြင်းအတွက် အမှန်တကယ် တုံ့ပြန်မှုတန်ဖိုး
• ŷ _i : Multiple linear regression model ကို အခြေခံ၍ ခန့်မှန်းထားသော တုံ့ပြန်မှုတန်ဖိုး

အပြန်အလှန်အားဖြင့် lasso regression သည် အောက်ပါတို့ကို လျှော့ချရန် ကြိုးပမ်းသည် ။

RSS + λΣ|β _j |

j သည် 1 မှ p ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် λ ≥ 0 ရှိရာသို့ သွားပါသည်။

ညီမျှခြင်းတွင် ဤဒုတိယအခေါ်အဝေါ်ကို ရုပ်သိမ်းပြစ်ဒဏ် ဟု ခေါ်သည်။ lasso regression တွင်၊ ဖြစ်နိုင်ခြေအနည်းဆုံး MSE (mean square error) test ကိုထုတ်ပေးသည့် λ အတွက် တန်ဖိုးတစ်ခုကို ရွေးပါသည်။

ဤသင်ခန်းစာသည် R တွင် lasso regression လုပ်ဆောင်ပုံအဆင့်ဆင့်ကို ဥပမာပေးထားသည်။

အဆင့် 1: ဒေတာကို တင်ပါ။

ဤဥပမာအတွက်၊ ကျွန်ုပ်တို့သည် mtcars ဟုခေါ်သော R ၏ built-in ဒေတာအတွဲကို အသုံးပြုပါမည်။ ကျွန်ုပ်တို့သည် တုံ့ပြန်မှု variable အဖြစ် hp ကို အသုံးပြုပြီး အောက်ပါ variable များကို ကြိုတင်ခန့်မှန်းသူများအဖြစ် အသုံးပြုပါမည်။

• စိုင်းစိုင်းခမ်းလှိုင်
• ကိုယ်အလေးချိန်
• ပြောရမှာပါ။
• qsec

lasso regression လုပ်ဆောင်ရန်၊ ကျွန်ုပ်တို့သည် glmnet ပက်ကေ့ခ်ျမှ လုပ်ဆောင်ချက်များကို အသုံးပြုပါမည်။ ဤပက်ကေ့ဂျ်တွင် တုံ့ပြန်မှုကိန်းရှင်သည် vector ဖြစ်ရန်နှင့် ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်အစုအစုသည် data.matrix အတန်းအစားဖြစ်ရန် လိုအပ်သည်။

အောက်ဖော်ပြပါ ကုဒ်သည် ကျွန်ုပ်တို့၏ဒေတာကို သတ်မှတ်ပုံဖော်ပြသည်-

 #define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

အဆင့် 2- Lasso Regression Model ကို အံကိုက်လုပ်ပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် lasso ဆုတ်ယုတ်မှုပုံစံနှင့် ကိုက်ညီရန် glmnet() လုပ်ဆောင်ချက်ကို အသုံးပြုပြီး alpha=1 ကို သတ်မှတ်ပေးပါမည်။

0 နှင့် ညီမျှသော alpha ကိုသတ်မှတ်ခြင်းသည် ridge regression ကိုအသုံးပြုခြင်းနှင့် ညီမျှပြီး 0 နှင့် 1 ကြားတန်ဖိုးတစ်ခုသို့ အယ်လ်ဖာသတ်မှတ်ခြင်းသည် elastic net ကိုအသုံးပြုခြင်းနှင့် ညီမျှကြောင်း သတိပြုပါ။  

lambda အတွက် မည်သည့်တန်ဖိုးကို အသုံးပြုရမည်ကို ဆုံးဖြတ်ရန်၊ ကျွန်ုပ်တို့သည် k-fold cross-validation ကို လုပ်ဆောင်ပြီး အနိမ့်ဆုံး test mean squared error (MSE) ကိုထုတ်ပေးသည့် lambda တန်ဖိုးကို ခွဲခြားသတ်မှတ်ပါမည်။

cv.glmnet() လုပ်ဆောင်ချက်သည် k = 10 ကြိမ်ကို အသုံးပြု၍ k-fold cross-validation အလိုအလျောက် လုပ်ဆောင်ကြောင်း သတိပြုပါ။

 library (glmnet)

#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 1 )

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda

[1] 5.616345

#produce plot of test MSE by lambda value
plot(cv_model) 

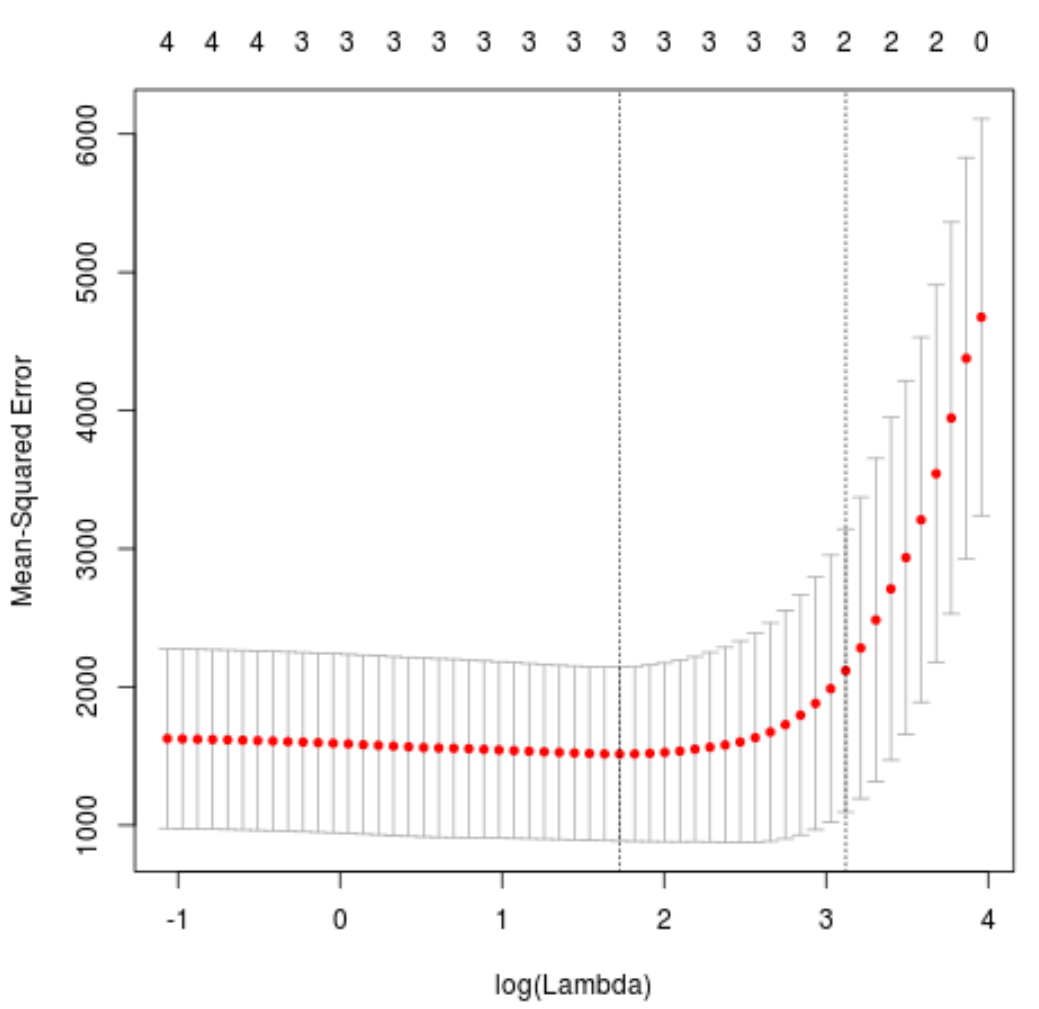
MSE စမ်းသပ်မှုကို လျှော့ချပေးသည့် lambda တန်ဖိုးသည် 5.616345 ဖြစ်သွားသည်။

အဆင့် 3- နောက်ဆုံးပုံစံကို ပိုင်းခြားစိတ်ဖြာပါ။

နောက်ဆုံးတွင်၊ အကောင်းဆုံးသော lambda တန်ဖိုးဖြင့် ထုတ်လုပ်ထားသော နောက်ဆုံးမော်ဒယ်ကို ပိုင်းခြားစိတ်ဖြာနိုင်ပါသည်။

ဤမော်ဒယ်အတွက် ကိန်းဂဏန်း ခန့်မှန်းချက်များကို ရယူရန် အောက်ပါကုဒ်ကို အသုံးပြုနိုင်ပါသည်။

 #find coefficients of best model
best_model <- glmnet(x, y, alpha = 1 , lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                   s0
(Intercept) 484.20742
mpg -2.95796
wt 21.37988
drat.      
qsec -19.43425

lasso regression သည် coefficient ကို သုညသို့ လျှော့ချပေးသောကြောင့် drat ခန့်မှန်းသူအတွက် coefficient မပြပါ။ ဆိုလိုသည်မှာ သူ့တွင် လုံလောက်သော လွှမ်းမိုးမှု မရှိသောကြောင့် မော်ဒယ်မှ လုံးဝ ဖယ်ရှားခံခဲ့ရခြင်း ဖြစ်သည်။

ဤသည်မှာ တောင်ကြောဆုတ်ယုတ်မှု နှင့် lasso ဆုတ်ယုတ်မှု ကြား အဓိကကွာခြားချက်ကို သတိပြုပါ။ Ridge regression သည် သုည ဆီသို့ coefficients အားလုံးကို လျှော့ချပေးသည်၊ သို့သော် lasso regression သည် coefficients ကို သုည အထိ လျှော့ချခြင်းဖြင့် မော်ဒယ်မှ ခန့်မှန်းသူများကို ဖယ်ရှားရန် အလားအလာရှိပါသည်။

လေ့လာတွေ့ရှိချက်အသစ်များနှင့်ပတ်သက်၍ ခန့်မှန်းချက်များပြုလုပ်ရန် နောက်ဆုံး lasso ဆုတ်ယုတ်မှုပုံစံကိုလည်း ကျွန်ုပ်တို့အသုံးပြုနိုင်ပါသည်။ ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် အောက်ပါအရည်အချင်းများရှိသော ကားအသစ်တစ်စီးရှိသည်ဆိုပါစို့။

• စိုင်းစိုင်းခမ်းလှိုင် : ၂၄
• အလေးချိန်: 2.5
• စျေးနှုန်း: 3.5
• qsec: 18.5

အောက်ပါကုဒ်သည် ဤလေ့လာတွေ့ရှိချက်အသစ်၏ hp တန်ဖိုးကို ခန့်မှန်းရန် တပ်ဆင်ထားသော lasso ဆုတ်ယုတ်မှုပုံစံကို မည်သို့အသုံးပြုရမည်ကို ပြသသည်-

 #define new observation
new = matrix(c(24, 2.5, 3.5, 18.5), nrow= 1 , ncol= 4 ) 

#use lasso regression model to predict response value
predict(best_model, s = best_lambda, newx = new)

[1,] 109.0842

ထည့်သွင်းထားသောတန်ဖိုးများပေါ်မူတည်၍ ဤကားသည် မြင်းကောင်ရေ တန်ဖိုး 109.0842 ရှိမည်ဟု မော်ဒယ်က ခန့်မှန်းသည်။

နောက်ဆုံးတွင်၊ သင်တန်းဒေတာတွင် မော်ဒယ်၏ R-squared ကို တွက်ချက်နိုင်သည်-

 #use fitted best model to make predictions
y_predicted <- predict (best_model, s = best_lambda, newx = x)

#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.8047064

R နှစ်ထပ်ကိန်းသည် 0.8047064 ဖြစ်သွားသည်။ ဆိုလိုသည်မှာ၊ အကောင်းဆုံးမော်ဒယ်သည် လေ့ကျင့်ရေးဒေတာ၏ တုံ့ပြန်မှုတန်ဖိုးများကွဲလွဲမှု 80.47% ကို ရှင်းပြနိုင်ခဲ့သည်။

ဤဥပမာတွင်အသုံးပြုထားသော R ကုဒ်အပြည့်အစုံကို ဤနေရာတွင် ရှာတွေ့နိုင်ပါသည်။