R တွင် တစ်ပြေးညီ ခွဲခြားမှု ခွဲခြမ်းစိတ်ဖြာခြင်း (တစ်ဆင့်ပြီးတစ်ဆင့်)

တစ်ပြေးညီ ခွဲခြားမှု ခွဲခြမ်းစိတ်ဖြာခြင်း သည် သင့်တွင် ကြိုတင်ခန့်မှန်းကိန်းရှင်များ အစုတစ်ခုရှိ၍ တုံ့ပြန်မှုကိန်းရှင်ကို အတန်းနှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော အတန်းအစားများအဖြစ် ခွဲခြားလိုသောအခါတွင် သင်သုံးနိုင်သော နည်းလမ်းတစ်ခုဖြစ်သည်။

ဤသင်ခန်းစာသည် R တွင် linear discriminant analysis ပြုလုပ်ပုံအဆင့်ဆင့်ကို ဥပမာပေးထားပါသည်။

အဆင့် 1- လိုအပ်သောစာကြည့်တိုက်များကို တင်ပါ။

ပထမဦးစွာ၊ ဤဥပမာအတွက် လိုအပ်သော စာကြည့်တိုက်များကို တင်ပေးပါမည်။

 library (MASS)
library (ggplot2)

အဆင့် 2: ဒေတာကို တင်ပါ။

ဤဥပမာအတွက်၊ R တွင်တည်ဆောက်ထားသော iris dataset ကိုကျွန်ုပ်တို့အသုံးပြုပါမည်။ အောက်ပါကုဒ်သည် ဤဒေတာအတွဲကိုမည်သို့တင်ရန်နှင့်ပြသရမည်ကိုပြသသည်-

 #attach iris dataset to make it easy to work with
attach(iris)

#view structure of dataset
str(iris)

'data.frame': 150 obs. of 5 variables:
 $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
 $ Sepal.Width: num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
 $Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
 $Petal.Width: num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
 $ Species: Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 ...

ဒေတာအတွဲတွင် ကိန်းရှင် ၅ ခုနှင့် စုစုပေါင်း စောင့်ကြည့်မှု ၁၅၀ ပါ၀င်ကြောင်း ကျွန်ုပ်တို့ တွေ့နိုင်ပါသည်။

ဤဥပမာအတွက်၊ ပေးထားသောပန်းအမျိုးအစားကို အမျိုးအစားခွဲခြားရန် linear discriminant analysis model တစ်ခုကို တည်ဆောက်ပါမည်။

ကျွန်ုပ်တို့သည် မော်ဒယ်တွင် အောက်ပါ ကြိုတင်ခန့်မှန်းကိန်းရှင်များကို အသုံးပြုပါမည်-

• Sepal.Length
• Sepal.Width
• ပန်းပွင့်။အရှည်
• ပန်းပွင့်။အကျယ်

အောက်ဖော်ပြပါ ဖြစ်နိုင်ချေရှိသော အတန်းသုံးမျိုးအား ပံ့ပိုးပေးသည့် Species response variable ကို ခန့်မှန်းရန် ၎င်းတို့ကို အသုံးပြုပါမည်။

• setosa
• စွယ်စုံရောင်
• ဗာဂျီးနီးယား

အဆင့် 3: ဒေတာကိုစကေးချပါ။

မျဉ်းကြောင်းခွဲခြားမှုခွဲခြမ်းစိတ်ဖြာမှု၏ အဓိကယူဆချက်တစ်ခုမှာ ခန့်မှန်းသူကိန်းရှင်တစ်ခုစီတွင် တူညီသောကွဲလွဲမှုရှိခြင်းပင်ဖြစ်သည်။ ဤယူဆချက်နှင့်ကိုက်ညီကြောင်းသေချာစေရန် ရိုးရှင်းသောနည်းလမ်းမှာ ကိန်းရှင်တစ်ခုစီတွင် ပျမ်းမျှ 0 နှင့် 1 ၏ စံသွေဖည်မှုရှိကြောင်း စကေးတိုင်းတာရန်ဖြစ်သည်။

scale() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ R တွင် လျင်မြန်စွာ လုပ်ဆောင်နိုင်သည်-

 #scale each predictor variable (ie first 4 columns)
iris[1:4] <- scale(iris[1:4])

ခန့်မှန်းသူ variable တစ်ခုစီတွင် 0 နှင့် စံသွေဖည်မှု 1 ရှိကြောင်း စစ်ဆေးရန် ကျွန်ုပ်တို့သည် apply() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်ပါသည်။

 #find mean of each predictor variable
apply(iris[1:4], 2, mean)

 Sepal.Length Sepal.Width Petal.Length Petal.Width 
-4.484318e-16 2.034094e-16 -2.895326e-17 -3.663049e-17 

#find standard deviation of each predictor variable
apply(iris[1:4], 2, sd) 

Sepal.Length Sepal.Width Petal.Length Petal.Width 
           1 1 1 1

အဆင့် 4- လေ့ကျင့်ရေးနှင့် စမ်းသပ်နမူနာများ ဖန်တီးပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် dataset အား မော်ဒယ်ကိုလေ့ကျင့်ရန် လေ့ကျင့်ရေးအစုတစ်ခုအဖြစ် ခွဲပြီး မော်ဒယ်အား စမ်းသပ်ရန်အတွက် စမ်းသပ်မှုတစ်ခုအဖြစ် ခွဲသွားပါမည်။

 #make this example reproducible
set.seed(1)

#Use 70% of dataset as training set and remaining 30% as testing set
sample <- sample(c( TRUE , FALSE ), nrow (iris), replace = TRUE , prob =c(0.7,0.3))
train <- iris[sample, ]
test <- iris[!sample, ] 

အဆင့် 5- LDA မော်ဒယ်ကို ချိန်ညှိပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏ဒေတာသို့ LDA မော်ဒယ်ကို လိုက်လျောညီထွေဖြစ်အောင် MASS အထုပ်မှ lda() လုပ်ဆောင်ချက်ကို အသုံးပြုပါမည်။

 #fit LDA model
model <- lda(Species~., data=train)

#view model output
model

Call:
lda(Species ~ ., data = train)

Prior probabilities of groups:
    setosa versicolor virginica 
 0.3207547 0.3207547 0.3584906 

Group means:
           Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa -1.0397484 0.8131654 -1.2891006 -1.2570316
versicolor 0.1820921 -0.6038909 0.3403524 0.2208153
virginica 0.9582674 -0.1919146 1.0389776 1.1229172

Coefficients of linear discriminants:
                    LD1 LD2
Sepal.Length 0.7922820 0.5294210
Sepal.Width 0.5710586 0.7130743
Petal.Length -4.0762061 -2.7305131
Petal.Width -2.0602181 2.6326229

Proportion of traces:
   LD1 LD2 
0.9921 0.0079 

မော်ဒယ်ရလဒ်များကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံမှာ အောက်ပါအတိုင်းဖြစ်သည်။

ကြိုတင်ဖြစ်နိုင်ချေများကို အုပ်စုဖွဲ့ပါ- ၎င်းတို့သည် လေ့ကျင့်ရေးအစုံရှိ မျိုးစိတ်တစ်ခုစီ၏ အချိုးအစားများကို ကိုယ်စားပြုသည်။ ဥပမာအားဖြင့်၊ လေ့ကျင့်မှုအစုံတွင် လေ့လာတွေ့ရှိချက်အားလုံး၏ ၃၅.၈%သည် virginica မျိုးစိတ်အတွက်ဖြစ်သည်။

အုပ်စုပျှမ်းမျှများ- ဤအရာများသည် မျိုးစိတ်တစ်ခုစီအတွက် ခန့်မှန်းပေးသူ variable တစ်ခုစီ၏ ပျမ်းမျှတန်ဖိုးများကို ဖော်ပြသည်။

Linear Discriminant Coefficients- ၎င်းတို့သည် LDA မော်ဒယ် ဆုံးဖြတ်ချက်စည်းမျဉ်းကို လေ့ကျင့်ရန် အသုံးပြုသည့် ကြိုတင်ခန့်မှန်းကိန်းရှင်များ ပေါင်းစပ်မှုကို ပြသသည်။ ဥပမာအားဖြင့်:

• LD1: 0.792 * sepal length + 0.571 * sepal width – 4.076 * ပွင့်ချပ်အရှည် – 2.06 * ပွင့်ချပ်အကျယ်
• LD2: 0.529 * sepal length + 0.713 * sepal width – 2.731 * ပွင့်ချပ်အရှည် + 2.63 * ပွင့်ချပ် အကျယ်

ခြေရာခံအချိုးအစား- ၎င်းတို့သည် မျဉ်းကြောင်းခွဲခြားမှုလုပ်ဆောင်မှုတစ်ခုစီမှရရှိသော ခွဲထွက်ခြင်းရာခိုင်နှုန်းကိုပြသသည်။

အဆင့် 6- ခန့်မှန်းချက်များကို ပြုလုပ်ရန် မော်ဒယ်ကို အသုံးပြုပါ။

ကျွန်ုပ်တို့၏လေ့ကျင့်ရေးဒေတာကို အသုံးပြု၍ မော်ဒယ်ကို တပ်ဆင်ပြီးသည်နှင့်၊ ကျွန်ုပ်တို့၏ စမ်းသပ်ဒေတာကို ခန့်မှန်းရန် ၎င်းကို အသုံးပြုနိုင်ပါသည်။

 #use LDA model to make predictions on test data
predicted <- predict (model, test)

names(predicted)

[1] "class" "posterior" "x"   

၎င်းသည် ကိန်းရှင် သုံးခုပါသော စာရင်းကို ပြန်ပေးသည်-

• အတန်း- ခန့်မှန်းထားသော အတန်း
• posterior- လေ့လာမှုတစ်ခုစီသည် အတန်းတစ်ခုစီနှင့်သက်ဆိုင်သည့် နောက်ဆက်တွဲဖြစ်နိုင်ခြေ
• x- တစ်ပြေးညီ ခွဲခြားမှုများ

ကျွန်ုပ်တို့၏ စမ်းသပ်ဒေတာအတွဲတွင် ပထမခြောက်ချက်လေ့လာချက်အတွက် ဤရလဒ်တစ်ခုစီကို ကျွန်ုပ်တို့ လျင်မြန်စွာမြင်ယောင်နိုင်သည်-

 #view predicted class for first six observations in test set
head(predicted$class)

[1] setosa setosa setosa setosa setosa setosa
Levels: setosa versicolor virginica

#view posterior probabilities for first six observations in test set
head(predicted$posterior)

   setosa versicolor virginica
4 1 2.425563e-17 1.341984e-35
6 1 1.400976e-21 4.482684e-40
7 1 3.345770e-19 1.511748e-37
15 1 6.389105e-31 7.361660e-53
17 1 1.193282e-25 2.238696e-45
18 1 6.445594e-22 4.894053e-41

#view linear discriminants for first six observations in test set
head(predicted$x)

         LD1 LD2
4 7.150360 -0.7177382
6 7.961538 1.4839408
7 7.504033 0.2731178
15 10.170378 1.9859027
17 8.885168 2.1026494
18 8.113443 0.7563902

LDA မော်ဒယ်သည် မျိုးစိတ်များကို မှန်ကန်စွာ ခန့်မှန်းပေးသည့် လေ့လာတွေ့ရှိမှု ရာခိုင်နှုန်းများအတွက် အောက်ပါကုဒ်ကို သုံးနိုင်သည်-

 #find accuracy of model
mean(predicted$class==test$Species)

[1] 1

ကျွန်ုပ်တို့၏စမ်းသပ်ဒေတာအတွဲရှိ စူးစမ်းလေ့လာမှုများ၏ 100% အတွက် မော်ဒယ်သည် မျိုးစိတ်များကို မှန်ကန်စွာ ခန့်မှန်းပေးကြောင်း ထွက်ပေါ်လာပါသည်။

လက်တွေ့ကမ္ဘာတွင်၊ LDA မော်ဒယ်သည် အတန်းတစ်ခုစီ၏ ရလဒ်များကို မှန်ကန်စွာ ခန့်မှန်းလေ့မရှိသော်လည်း ဤမျက်ဝန်းဒေတာအတွဲကို စက်သင်ယူမှု အယ်လဂိုရီသမ်များ ကောင်းမွန်စွာလုပ်ဆောင်လေ့ရှိသည့် နည်းလမ်းဖြင့် ရိုးရိုးရှင်းရှင်းတည်ဆောက်ထားသည်။

အဆင့် 7- ရလဒ်များကို မြင်ယောင်ကြည့်ပါ။

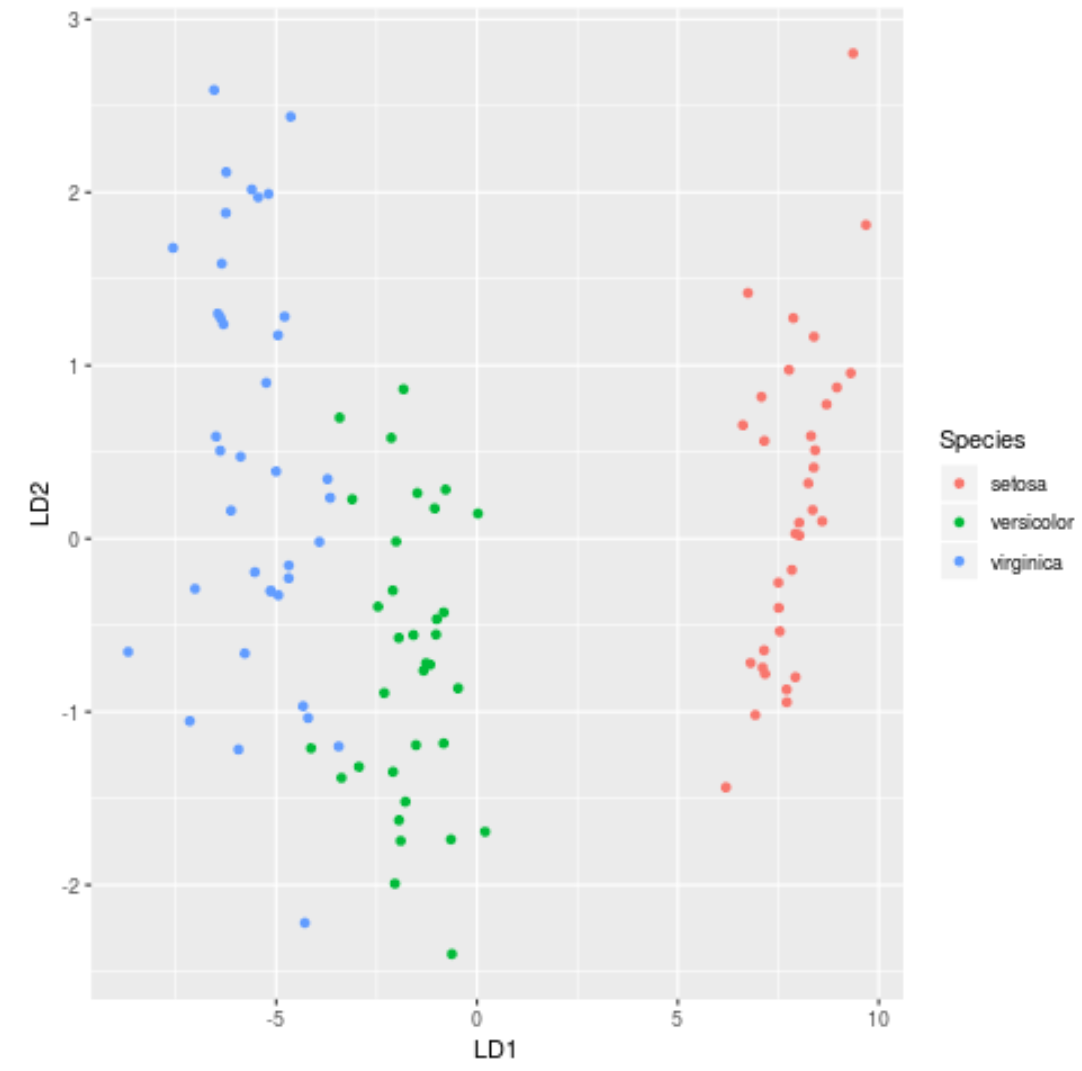
နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် မော်ဒယ်၏ တစ်ပြေးညီ ခွဲခြားဆက်ဆံမှုများကို မြင်သာစေရန် LDA ကြံစည်မှုကို ဖန်တီးနိုင်ပြီး ကျွန်ုပ်တို့၏ဒေတာအတွဲတွင် မတူညီသောမျိုးစိတ်သုံးမျိုးကို မည်မျှကောင်းစွာ ပိုင်းခြားထားသည်ကို မြင်ယောင်နိုင်သည်-

 #define data to plot
lda_plot <- cbind(train, predict(model)$x)

#createplot
ggplot(lda_plot, aes (LD1, LD2)) +
  geom_point( aes (color=Species))

ဤသင်ခန်းစာတွင်အသုံးပြုထားသော R ကုဒ်အပြည့်အစုံကို ဤနေရာတွင် သင်တွေ့နိုင်ပါသည်။