R ရှိ k-medoids- အဆင့်ဆင့် ဥပမာ
Clustering သည် ဒေတာအတွဲတစ်ခုအတွင်း အုပ်စုများ သို့မဟုတ် စောင့်ကြည့်မှု အစုအဝေးများကို ရှာဖွေရန် ကြိုးစားသည့် စက်သင်ယူမှုနည်းပညာတစ်ခုဖြစ်သည်။
ရည်ရွယ်ချက်မှာ အစုအဝေးတစ်ခုစီအတွင်းရှိ ရှုမြင်သုံးသပ်ချက်များသည် တစ်ခုနှင့်တစ်ခု အလွန်တူညီပြီး ကွဲပြားသောအစုအဝေးရှိ လေ့လာတွေ့ရှိချက်များသည် တစ်ခုနှင့်တစ်ခု အလွန်ကွဲပြားသည့် အစုအဝေးများကို ရှာဖွေရန်ဖြစ်သည်။
Clustering သည် တုံ့ပြန်မှုကိန်းရှင် ၏တန်ဖိုးကို ခန့်မှန်းမည့်အစား ဒေတာအတွဲတစ်ခုအတွင်း ဖွဲ့စည်းပုံကိုရှာဖွေရန် ရိုးရိုးရှင်းရှင်းကြိုးစားနေသောကြောင့် ကြီးကြပ်ခြင်းမရှိသော သင်ယူမှု ပုံစံတစ်ခုဖြစ်သည်။
လုပ်ငန်းများသည် အောက်ပါကဲ့သို့သော အချက်အလက်များကို ရယူသည့်အခါတွင် စျေးကွက်ရှာဖွေရေးတွင် Clustering ကို အသုံးများပါသည်။
- အိမ်ထောင်စုဝင်ငွေ
- အိမ်ထောင်စု အရွယ်အစား
- အိမ်ထောင်ဦးစီး အတတ်ပညာ
- အနီးဆုံးမြို့ပြဧရိယာအကွာအဝေး
ဤအချက်အလက်ကို ရနိုင်သည့်အခါ၊ အလားတူအိမ်ထောင်စုများကို ခွဲခြားသတ်မှတ်ရန် အစုလိုက်အပြုံလိုက်ကို အသုံးပြုနိုင်ပြီး အချို့သောထုတ်ကုန်များကို ဝယ်ယူရန် သို့မဟုတ် ကြော်ငြာအမျိုးအစားကို ပိုမိုကောင်းမွန်စွာ တုံ့ပြန်နိုင်ခြေပိုများနိုင်သည်။
အစုလိုက်ဖွဲ့ခြင်း၏ အသုံးအများဆုံးပုံစံများထဲမှ တစ်ခုမှာ k-means အစုအဝေး ဟု ခေါ်သည်။
ကံမကောင်းစွာဖြင့်၊ ဤနည်းလမ်းကို outliers များမှ လွှမ်းမိုးနိုင်သည်၊ ထို့ကြောင့် အသုံးများသော အခြားရွေးချယ်စရာတစ်ခုမှာ k-medoids clustering ဖြစ်သည်။
K-Medoids အစုလိုက်အပြုံလိုက်ဆိုတာဘာလဲ။
K-medoids clustering သည် K အစုအဝေးများထဲမှ တစ်ခုသို့ ဒေတာအတွဲတစ်ခုအတွင်း စောင့်ကြည့်မှုတစ်ခုစီကို ထားရှိပေးသည့် နည်းလမ်းတစ်ခုဖြစ်သည်။
အဆုံးပန်းတိုင်သည် အစုအဝေးတစ်ခုစီရှိ အစုအဝေးတစ်ခုစီအတွင်း စောင့်ကြည့်မှုများသည် တစ်ခုနှင့်တစ်ခု အတော်လေးဆင်တူသည့် K အစုအဝေးများ ရှိရန်ဖြစ်သည်။
လက်တွေ့တွင်၊ ကျွန်ုပ်တို့သည် K-Means အစုအဝေးပြုလုပ်ရန် အောက်ပါအဆင့်များကို အသုံးပြုသည်-
1. K အတွက် တန်ဖိုးတစ်ခုကို ရွေးပါ။
- ပထမဦးစွာ၊ ကျွန်ုပ်တို့သည် ဒေတာတွင် ကျွန်ုပ်တို့သတ်မှတ်လိုသည့် အစုအဝေးမည်မျှရှိသည်ကို ဆုံးဖြတ်ရန် လိုအပ်သည်။ မကြာခဏဆိုသလို ကျွန်ုပ်တို့သည် K အတွက် မတူညီသောတန်ဖိုးများစွာကို စမ်းသပ်ပြီး ပေးထားသောပြဿနာတစ်ခုအတွက် အသင့်လျော်ဆုံးဖြစ်ဟန်ရှိသည့် အစုအဝေးအရေအတွက်ကို သိရှိနိုင်ရန် ရလဒ်များကို ခွဲခြမ်းစိတ်ဖြာရန် လိုအပ်ပါသည်။
2. စောင့်ကြည့်မှုတစ်ခုစီကို 1 မှ K မှ ကနဦးအစုအဝေးတစ်ခုသို့ ကျပန်းသတ်မှတ်ပါ။
3. အစုအဖွဲ့တာဝန်များ မပြောင်းလဲမချင်း အောက်ပါလုပ်ငန်းစဉ်များကို လုပ်ဆောင်ပါ။
- K အစုအဝေးတစ်ခုစီအတွက်၊ အစုအဝေး၏ ဆွဲငင်အားဗဟိုကို တွက်ချက်ပါ။ ဤသည်မှာ k th အစုအဝေး၏ လေ့လာတွေ့ရှိချက်များအတွက် အင်္ဂါရပ်များ၏ p medians ၏ vector ဖြစ်သည်။
- စောင့်ကြည့်မှုတစ်ခုစီကို အနီးစပ်ဆုံး အလယ်ဗဟိုဖြင့် အစုအဝေးသို့ သတ်မှတ်ပေးပါ။ ဤတွင်၊ အနီးစပ်ဆုံး ကို Euclidean အကွာအဝေးကို အသုံးပြု၍ သတ်မှတ်သည်။
နည်းပညာမှတ်စု-
k-medoids သည် အဓိပ္ပါယ်ထက် မီဒီယံများကို အသုံးပြု၍ အစုလိုက် အလယ်တန်းများကို တွက်ချက်သောကြောင့်၊ ၎င်းသည် k-ဆိုလိုသည်ထက် အကြမ်းဖျဉ်းအားဖြင့် ပိုအားကောင်းတတ်သည်။
လက်တွေ့တွင်၊ ဒေတာအတွဲတွင် လွန်ကဲသောအစွန်းအထင်းများမရှိပါက၊ k-mean နှင့် k-medoids များသည် အလားတူရလဒ်များကို ထုတ်ပေးမည်ဖြစ်ပါသည်။
R တွင် အစုလိုက်အပြုံလိုက် K-Medoids
အောက်ဖော်ပြပါ သင်ခန်းစာသည် R တွင် k-medoids အစုလိုက်ပြုလုပ်ပုံအဆင့်ဆင့်ကို ဥပမာပေးထားပါသည်။
အဆင့် 1- လိုအပ်သော ပက်ကေ့ခ်ျများကို တင်ပါ။
ဦးစွာ၊ R တွင် k-medoids အစုအဝေးအတွက် အသုံးဝင်သောလုပ်ဆောင်ချက်များစွာပါရှိသော ပက်ကေ့ခ်ျနှစ်ခုကို ကျွန်ုပ်တို့ တင်ပါမည်။
library (factoextra) library (cluster)
အဆင့် 2: ဒေတာကိုတင်ပြီး ပြင်ဆင်ပါ။
ဤဥပမာအတွက်၊ လူသတ်မှု ၊ ချေမှုန်းရေး နှင့် မုဒိမ်းမှုများ အတွက် 1973 ခုနှစ်တွင် အမေရိကန်ပြည်နယ်တစ်ခုစီရှိ လူ 100,000 တစ်ဦးလျှင် ဖမ်းဆီးခံရမှု အရေအတွက်ပါဝင်သည့် R တွင်တည်ဆောက်ထားသော USArrests ဒေတာအစုံကို ကျွန်ုပ်တို့အသုံးပြုမည်ဖြစ်ပြီး၊ မြို့ပြတွင်နေထိုင်သော ပြည်နယ်တစ်ခုစီ၏ လူဦးရေရာခိုင်နှုန်း ဒေသများ။ ၊ UrbanPop
အောက်ပါ ကုဒ်သည် အောက်ပါအတိုင်း ပြုလုပ်နည်းကို ပြသသည် ။
- USArrests ဒေတာအတွဲကို တင်ပါ။
- ပျောက်ဆုံးနေသောတန်ဖိုးများဖြင့် အတန်းအားလုံးကို ဖယ်ရှားပါ။
- 0 mean of 0 နှင့် standard deviation ကို 1 ရှိရန် dataset အတွင်းရှိ variable တစ်ခုစီကို အတိုင်းအတာ
#load data df <-USArrests #remove rows with missing values df <- na. omitted (df) #scale each variable to have a mean of 0 and sd of 1 df <- scale(df) #view first six rows of dataset head(df) Murder Assault UrbanPop Rape Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473 Alaska 0.50786248 1.1068225 -1.2117642 2.484202941 Arizona 0.07163341 1.4788032 0.9989801 1.042878388 Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602 California 0.27826823 1.2628144 1.7589234 2.067820292 Colorado 0.02571456 0.3988593 0.8608085 1.864967207
အဆင့် 3- အကောင်းဆုံးအစုအဝေးအရေအတွက်ကို ရှာပါ။
R တွင် k-medoid အစုလိုက်အပြုံလိုက်လုပ်ဆောင်ရန်၊ ကျွန်ုပ်တို့သည် “မီဒီယံများကို ပိုင်းခြားခြင်း” အတွက် အတိုကောက်အဓိပ္ပာယ်ဆောင်သည့် pam() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်ပြီး အောက်ပါ syntax ကို အသုံးပြုနိုင်ပါသည်။
pam(ဒေတာ၊ k၊ မက်ထရစ် = “ ယူကလစ်” ၊ ရပ်တည်ချက် = FALSE)
ရွှေ-
- ဒေတာ- ဒေတာအတွဲအမည်။
- k- အစုအဝေးအရေအတွက်။
- မက်ထရစ်- အကွာအဝေးကို တွက်ချက်ရန် အသုံးပြုရန် မက်ထရစ်။ ပုံသေသည် ယူကလိဒ် ဖြစ်သော်လည်း သင်သည် မန်ဟက်တန်ကို သတ်မှတ်နိုင်သည်။
- ရပ်တည်ချက်- ဒေတာအတွဲရှိ ကိန်းရှင်တစ်ခုစီကို ပုံမှန်ဖြစ်စေရန်၊ မူရင်းတန်ဖိုးသည် မှားနေသည်။
ဘယ်အစုအဖွဲ့ အရေအတွက်က အကောင်းဆုံးဖြစ်မလဲဆိုတာ ကြိုမသိသေးတဲ့အတွက်၊ ဆုံးဖြတ်ရာမှာ ကူညီပေးနိုင်တဲ့ မတူညီတဲ့ ဂရပ်နှစ်ခုကို ဖန်တီးပေးမှာဖြစ်ပါတယ်-
1. စတုရန်းများပေါင်းစုခြင်း စုစုပေါင်းနှင့် ဆက်စပ်သော အစုအဝေးအရေအတွက်
ပထမဦးစွာ၊ ကျွန်ုပ်တို့သည် fviz_nbclust() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ စတုရန်း၏ပေါင်းလဒ်အတွင်းရှိ စုစုပေါင်းအစုများနှင့် အစုအဝေးအရေအတွက်နှင့် ကိန်းဂဏန်းတစ်ခုကို ဖန်တီးရန်။
fviz_nbclust(df, pam, method = “ wss ”)
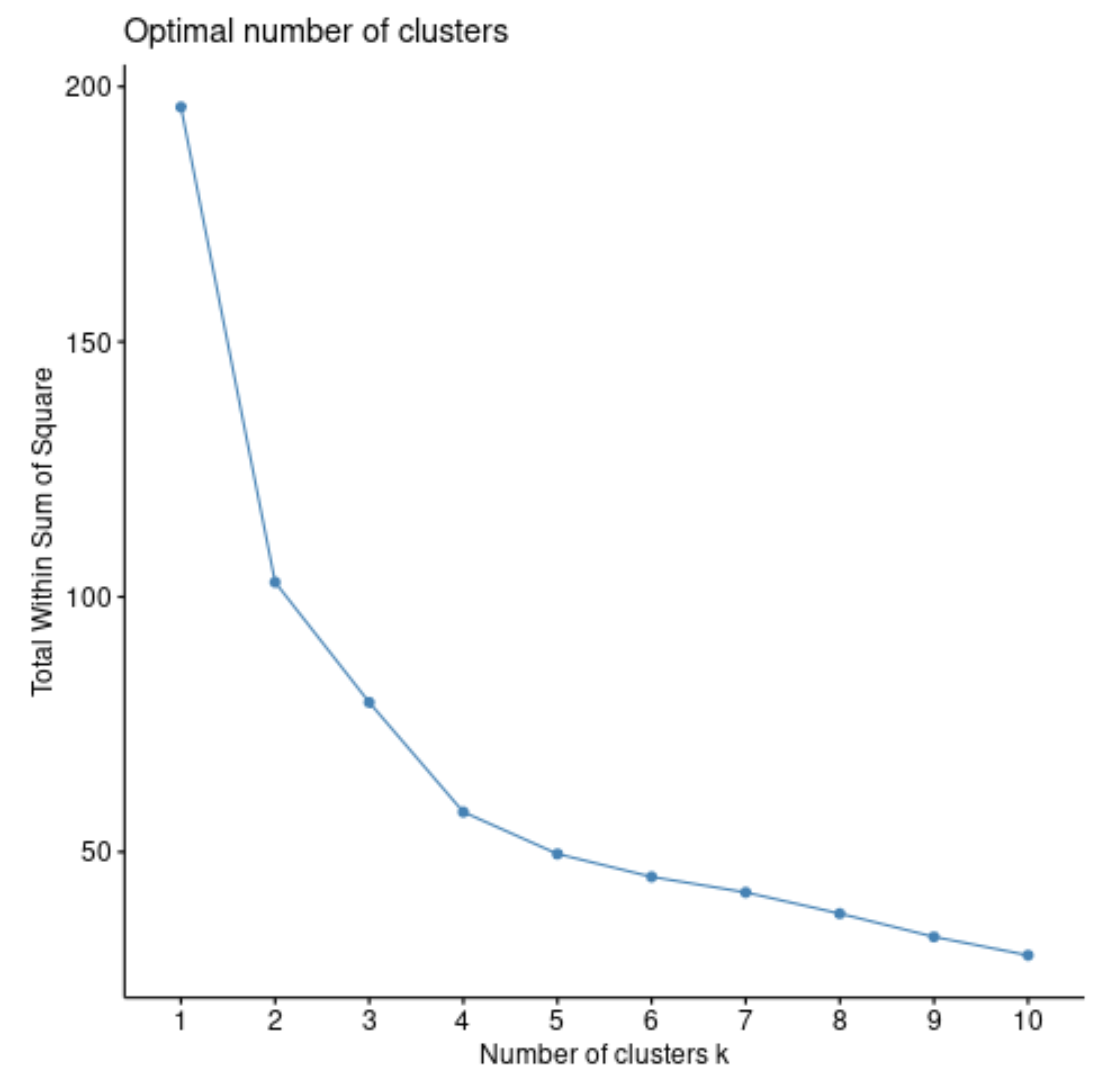
ကျွန်ုပ်တို့သည် အစုအဝေးအရေအတွက်ကို တိုးလာသည်နှင့်အမျှ စတုရန်း၏ပေါင်းလဒ်စုစုပေါင်းသည် ယေဘူယျအားဖြင့် အမြဲတိုးနေလိမ့်မည်။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် ဤဇာတ်ကွက်အမျိုးအစားကို ဖန်တီးသောအခါ၊ စတုရန်းများပေါင်းလဒ်သည် “ကွေးသည်” သို့မဟုတ် အဆင့်မှစတင်သည့် “ ဒူး” ကို ရှာဖွေနေပါသည်။
ကွက်ကွက်၏ ကွေးကောက်သောအမှတ်သည် ယေဘုယျအားဖြင့် အကောင်းဆုံးအစုအစည်းများ၏ အရေအတွက်နှင့် သက်ဆိုင်သည်။ ဤကိန်းဂဏန်းထက် လွန်ကဲစွာ ဝတ်ဆင် နိုင်ဖွယ်ရှိသည်။
ဤဂရပ်အတွက်၊ k = 4 အစုအဝေးတွင် သေးငယ်သော အကွေးအကောက်တစ်ခု သို့မဟုတ် “ ကွေး” ရှိသည်ကို တွေ့ရပါသည်။
2. အစုအဝေးအရေအတွက်နှင့် ကွာဟချက်စာရင်းဇယား
အစုအဝေးများ၏ အကောင်းဆုံးအရေအတွက်ကို ဆုံးဖြတ်ရန် အခြားနည်းလမ်းမှာ ကွဲပြားမှုမရှိဘဲ ဖြန့်ဖြူးမှုအတွက် ၎င်းတို့၏မျှော်လင့်ထားသည့်တန်ဖိုးများနှင့် ကွဲပြားသော k ၏ စုစုပေါင်းအတွင်းအစုအစည်းအကွဲကွဲကွဲပြားမှုကို နှိုင်းယှဉ်သည့် deviation statistic ဟုခေါ်သော မက်ထရစ်ကိုအသုံးပြုခြင်းဖြစ်သည်။
fviz_gap_stat() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ အစု အဝေးမှ clusGap( ) လုပ်ဆောင်ချက်ကို အသုံးပြု၍ အစုအစည်းများ၏ အရေအတွက်တစ်ခုစီအတွက် ကွာဟချက်စာရင်းဇယားကို တွက်ချက်နိုင်သည်-
#calculate gap statistic based on number of clusters gap_stat <- clusGap(df, FUN = pam, K.max = 10, #max clusters to consider B = 50) #total bootstrapped iterations #plot number of clusters vs. gap statistic fviz_gap_stat(gap_stat)
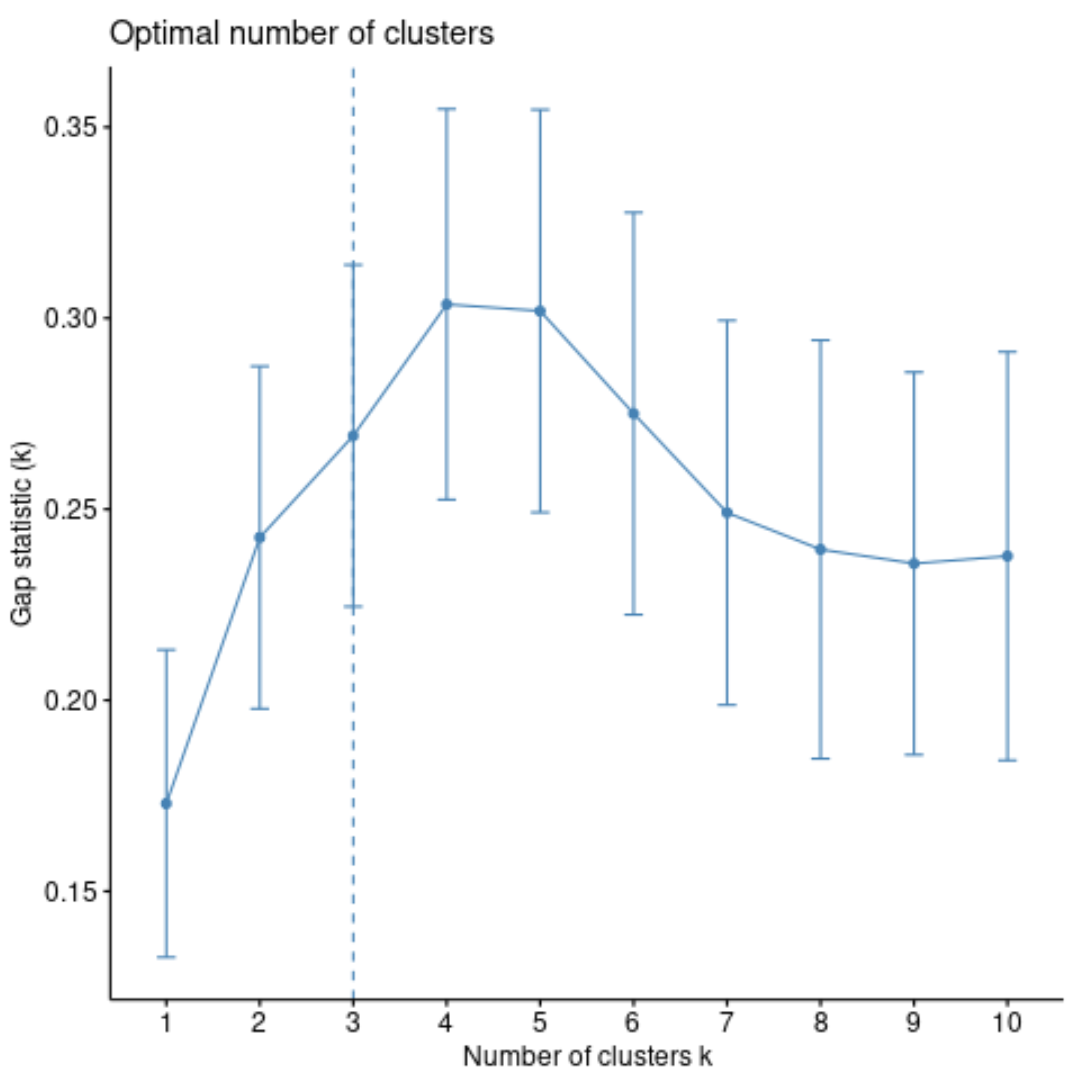
ဂရပ်ဖ်မှ၊ ကွာဟချက်စာရင်းဇယားသည် k = 4 အစုအဝေးတွင် အမြင့်ဆုံးဖြစ်သည်၊ ၎င်းသည် ယခင်က ကျွန်ုပ်တို့အသုံးပြုခဲ့သော တံတောင်ဆစ်နည်းလမ်းနှင့် ကိုက်ညီကြောင်း ကျွန်ုပ်တို့တွေ့နိုင်သည်။
အဆင့် 4- Optimal K ဖြင့် K-Medoids အစုအဝေးကို လုပ်ဆောင်ပါ။
နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် k ၏ အကောင်းဆုံးတန်ဖိုးကို အသုံးပြု၍ ဒေတာအတွဲပေါ်တွင် k-medoids အစုအဝေးကို လုပ်ဆောင်နိုင်သည်-
#make this example reproducible set.seed(1) #perform k-medoids clustering with k = 4 clusters kmed <- pam(df, k = 4) #view results kmed ID Murder Assault UrbanPop Rape Alabama 1 1.2425641 0.7828393 -0.5209066 -0.003416473 Michigan 22 0.9900104 1.0108275 0.5844655 1.480613993 Oklahoma 36 -0.2727580 -0.2371077 0.1699510 -0.131534211 New Hampshire 29 -1.3059321 -1.3650491 -0.6590781 -1.252564419 Vector clustering: Alabama Alaska Arizona Arkansas California 1 2 2 1 2 Colorado Connecticut Delaware Florida Georgia 2 3 3 2 1 Hawaii Idaho Illinois Indiana Iowa 3 4 2 3 4 Kansas Kentucky Louisiana Maine Maryland 3 3 1 4 2 Massachusetts Michigan Minnesota Mississippi Missouri 3 2 4 1 3 Montana Nebraska Nevada New Hampshire New Jersey 3 3 2 4 3 New Mexico New York North Carolina North Dakota Ohio 2 2 1 4 3 Oklahoma Oregon Pennsylvania Rhode Island South Carolina 3 3 3 3 1 South Dakota Tennessee Texas Utah Vermont 4 1 2 3 4 Virginia Washington West Virginia Wisconsin Wyoming 3 3 4 4 3 Objective function: build swap 1.035116 1.027102 Available components: [1] "medoids" "id.med" "clustering" "objective" "isolation" [6] "clusinfo" "silinfo" "diss" "call" "data"
အစုအဝေး လေးခုလုံးသည် ဒေတာအတွဲအတွင်း အမှန်တကယ် လေ့လာတွေ့ရှိချက်များဖြစ်ကြောင်း သတိပြုပါ။ အထွက်၏ထိပ်အနီးတွင် အလယ်ဗဟိုလေးခုသည် အောက်ပါပြည်နယ်များဖြစ်ကြောင်း ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်-
- ဘားမား
- မီရှီဂန်
- ဟိုး
- New Hampshire
fivz_cluster() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ axes ပေါ်ရှိ ပထမအဓိကအစိတ်အပိုင်းနှစ်ခုကိုပြသသည့် scatterplot တွင် အစုအဝေးများကို မြင်ယောင်နိုင်သည်-
#plot results of final k-medoids model
fviz_cluster(kmed, data = df)
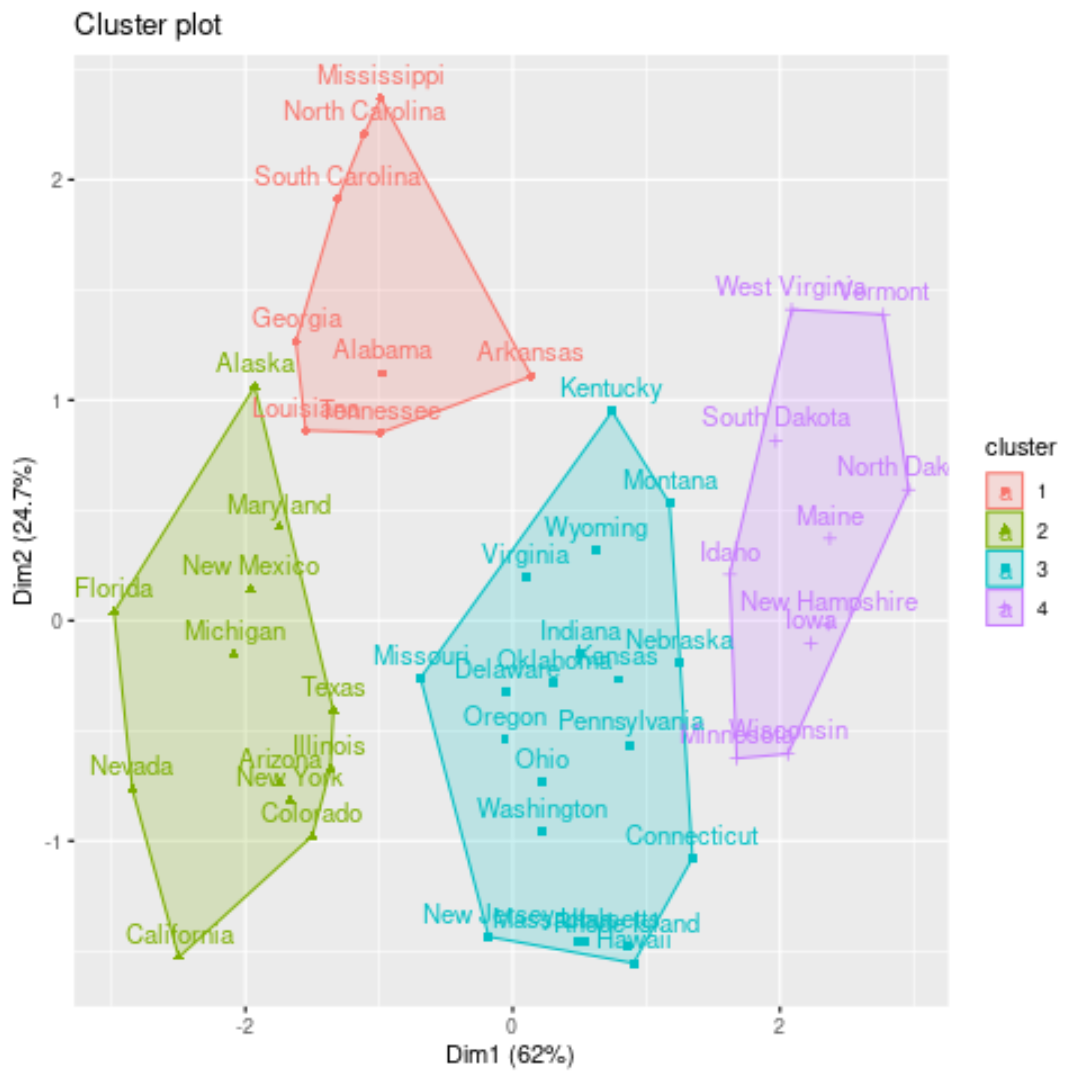
ပြည်နယ်တစ်ခုစီ၏ အစုအဝေးတာဝန်များကို မူရင်းဒေတာအတွဲသို့လည်း ထည့်နိုင်သည်။
#add cluster assignment to original data
final_data <- cbind(USArrests, cluster = kmed$cluster)
#view final data
head(final_data)
Murder Assault UrbanPop Rape cluster
Alabama 13.2 236 58 21.2 1
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 1
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2
ဤဥပမာတွင်အသုံးပြုထားသော R ကုဒ်အပြည့်အစုံကို ဤနေရာတွင် ရှာတွေ့နိုင်ပါသည်။