R နှင့် r-square- ကွာခြားချက်ကား အဘယ်နည်း။

စာရင်းအင်းများတွင် ကျောင်းသားများ မကြာခဏ ရောထွေးနေသော ဝေါဟာရ နှစ်ခုမှာ R နှင့် R-squared ဖြစ်ပြီး ^{R2 ဟု} ရေးလေ့ရှိသည်။

ရိုးရှင်းသော linear regression ၏အခြေအနေတွင်၊

• A- ကြိုတင်ခန့်မှန်းကိန်းရှင်၊ x နှင့် တုံ့ပြန်မှုကိန်းရှင် y တို့ကြား ဆက်စပ်မှု။
• R ² : ဆုတ်ယုတ်မှုပုံစံရှိ ကြိုတင်ခန့်မှန်းကိန်းရှင်က ရှင်းပြနိုင်သည့် တုံ့ပြန်မှုကိန်းရှင်တွင် ကွဲလွဲမှု၏အချိုးအစား။

ပြီးတော့ multiple linear regression ရဲ့ အခြေအနေမှာ၊

• A: တုံ့ပြန်မှုကိန်းရှင်၏ လေ့လာတွေ့ရှိထားသော တန်ဖိုးများနှင့် မော်ဒယ်မှ ပြုလုပ်ထားသည့် တုံ့ပြန်မှုကိန်းရှင်၏ ခန့်မှန်းတန်ဖိုးများကြား ဆက်စပ်မှု။
• R ² : ဆုတ်ယုတ်မှုပုံစံ၏ ကြိုတင်ခန့်မှန်းကိန်းရှင်များဖြင့် ရှင်းပြနိုင်သည့် တုံ့ပြန်မှုကိန်းရှင်၏ ကွဲလွဲမှုအချိုးအစား။

R ² ၏တန်ဖိုးသည် 0 နှင့် 1 အကြားရှိသည်ကို သတိပြုပါ။ တန်ဖိုးသည် 1 နှင့် ပိုနီးစပ်လေ၊ ခန့်မှန်းသူကိန်းရှင်(များ) နှင့် တုံ့ပြန်မှုကိန်းရှင်ကြား ဆက်နွယ်မှုအားကောင်းလေဖြစ်သည်။

အောက်ဖော်ပြပါ ဥပမာများသည် R နှင့် R-squared တန်ဖိုးများကို ရိုးရှင်းသော linear regression နှင့် multiple linear regression model များတွင် မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုသည်ကို ပြသထားသည်။

ဥပမာ 1- ရိုးရှင်းသော linear regression

သင်္ချာသင်တန်းတစ်ခုတွင် ကျောင်းသား 12 ဦးရရှိသော စာမေးပွဲရမှတ်များနှင့် နာရီများကိုပြသသည့် အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။

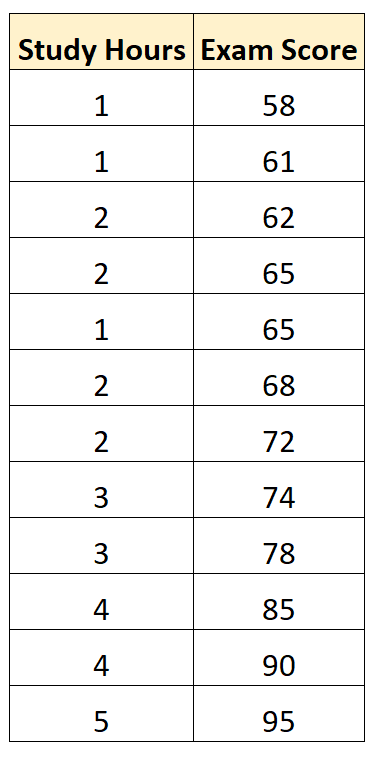
စာရင်းအင်းဆော့ဖ်ဝဲလ် (Excel၊ R၊ Python၊ SPSS စသည်ဖြင့်) ကိုအသုံးပြု၍ ကျွန်ုပ်တို့သည် ခန့်မှန်းကိန်းရှင်ကိန်းရှင်နှင့် “ စာမေးပွဲအဆင့်” အဖြစ် “ လေ့လာမှုနာရီ” ကို အသုံးပြု၍ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံ ကို တုံ့ပြန်မှုကိန်းရှင် အဖြစ် “ စာမေးပွဲအဆင့်” ကို အသုံးပြု၍ ကိုက်ညီနိုင်ပါသည်။

ဤမော်ဒယ်အတွက် အောက်ပါအထွက်ကို ကျွန်ုပ်တို့ ရှာတွေ့နိုင်သည်-

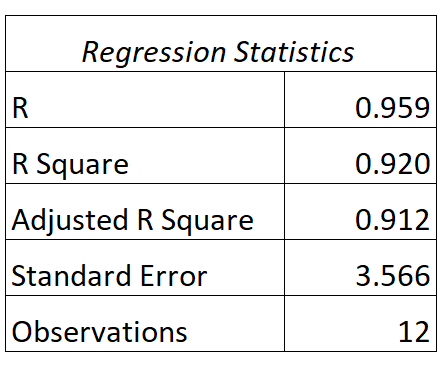
ဤမော်ဒယ်၏ R နှင့် R နှစ်ထပ်တန်ဖိုးများကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံမှာ အောက်ပါအတိုင်းဖြစ်သည် ။

• A- ဖြေဆိုချိန်နှင့် စာမေးပွဲရမှတ်ကြား ဆက်စပ်မှုမှာ 0.959 ဖြစ်သည်။
• R ² : ဤဆုတ်ယုတ်မှုပုံစံအတွက် R နှစ်ထပ်ကိန်းသည် 0.920 ဖြစ်သည်။ စာမေးပွဲရမှတ်များတွင် ကွဲလွဲမှု 92.0% ကို လေ့လာသည့် နာရီအရေအတွက်ဖြင့် ရှင်းပြနိုင်သည်ဟု ၎င်းကဆိုသည်။

R ² တန်ဖိုးသည် R တန်ဖိုးနှင့် နှစ်ထပ်ကိန်းတူညီကြောင်းကိုလည်း သတိပြုပါ။

^R2 = R * R = 0.959 * 0.959 = 0.920

ဥပမာ 2- Multiple linear regression

သင်္ချာသင်တန်းတစ်ခုတွင် ကျောင်းသား 12 ဦးရရှိသော လက်ရှိကျောင်းသားအဆင့်နှင့် စာမေးပွဲအဆင့်တို့ကို ပြသသည့် အောက်ပါဒေတာအတွဲ ရှိသည်ဆိုပါစို့။

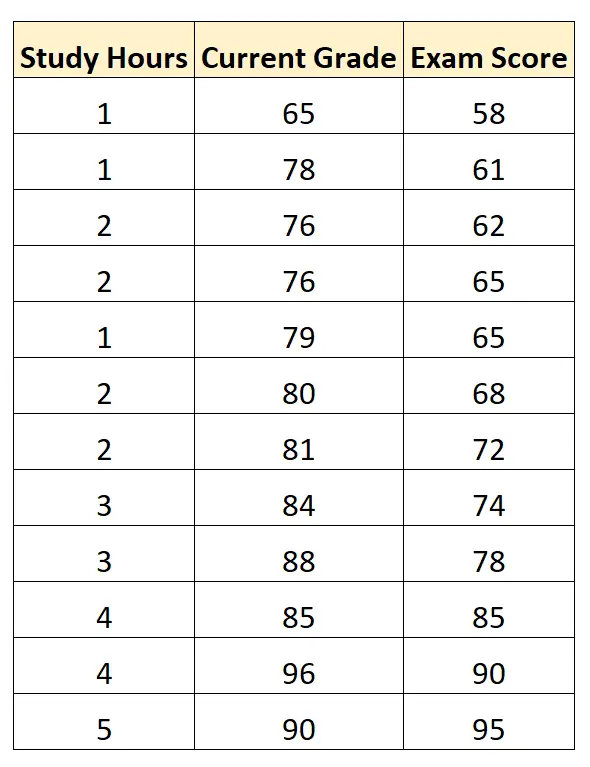
စာရင်းအင်းဆော့ဖ်ဝဲလ်ကိုအသုံးပြုခြင်းဖြင့် ကျွန်ုပ်တို့သည် ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် “စာမေးပွဲအဆင့်” တို့ကဲ့သို့ “ လေ့လာမှုနာရီ” နှင့် “ လက်ရှိအဆင့်” ကို အသုံးပြု၍ များစွာသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံကို ကျွန်ုပ်တို့ အံဝင်ခွင်ကျဖြစ်စေနိုင်သည်။

ဤမော်ဒယ်အတွက် အောက်ပါအထွက်ကို ကျွန်ုပ်တို့ ရှာတွေ့နိုင်သည်-

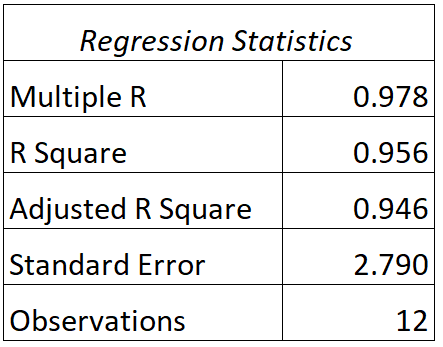
ဤမော်ဒယ်၏ R နှင့် R နှစ်ထပ်တန်ဖိုးများကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံမှာ အောက်ပါအတိုင်းဖြစ်သည် ။

• A- အမှန်တကယ် စာမေးပွဲရမှတ်များနှင့် မော်ဒယ်၏ ခန့်မှန်းစမ်းသပ်ရမှတ်များအကြား ဆက်စပ်မှုမှာ 0.978 ဖြစ်သည်။
• R ² : ဤဆုတ်ယုတ်မှုပုံစံအတွက် R နှစ်ထပ်ကိန်းသည် 0.956 ဖြစ်သည်။ ၎င်းသည် ကျွန်ုပ်တို့အား စာမေးပွဲရမှတ်များတွင် ကွဲလွဲမှု 95.6% ကို လေ့လာသည့် နာရီအရေအတွက်နှင့် အတန်းရှိ ကျောင်းသား၏ လက်ရှိအဆင့်ဖြင့် ရှင်းပြနိုင်ပါသည်။

R ² တန်ဖိုးသည် R တန်ဖိုးနှင့် နှစ်ထပ်ကိန်း တူညီကြောင်းကိုလည်း သတိပြုပါ။

^R2 = R * R = 0.978 * 0.978 = 0.956

ထပ်လောင်းအရင်းအမြစ်များ

ကောင်းသော R-squared တန်ဖိုးဆိုသည်မှာ အဘယ်နည်း။
Sum of Squares အတွက် နူးညံ့သောလမ်းညွှန်ချက်- SST၊ SSR၊ SSE