R တွင် bonferroni အမှားပြင်ဆင်နည်း

တစ်လမ်းသွား ANOVA ကို သုံးသော သို့မဟုတ် ထို့ထက်ပိုသော လွတ်လပ်သော အုပ်စုများကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားမှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည်။

ANOVA ဇယား၏ စုစုပေါင်း p-value သည် အချို့သော အရေးပါမှုအဆင့်အောက်တွင် ရှိနေပါက၊ အနည်းဆုံး အုပ်စု၏ ဆိုလိုရင်းမှာ အခြားနည်းများနှင့် ကွဲပြားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထားရှိသည်။

သို့သော် မည်သည့် အဖွဲ့များ အချင်းချင်း ကွဲပြားသည်ကို ဤအရာက ကျွန်ုပ်တို့အား မပြောပါ။ ၎င်းသည် ကျွန်ုပ်တို့အား အုပ်စု ပျမ်းမျှ ပျမ်းမျှအားလုံး မညီမျှကြောင်း ရိုးရှင်းစွာ ပြောပြသည်။

မိသားစုအလိုက် အမှားအယွင်း နှုန်းကို ထိန်းချုပ်ထားစဉ်တွင် မည်သည့်အဖွဲ့များ တစ်ခုနှင့်တစ်ခု ကွဲပြားသည်ကို အတိအကျ သိရှိရန်အတွက်၊ ကျွန်ုပ်တို့သည် မိသားစုအလိုက် အမှားအယွင်းနှုန်းကို ထိန်းချုပ်နေစဉ်တွင် အုပ်စုတစ်ခုစီကြားတွင် အတွဲလိုက် t-tests များကို လုပ်ဆောင်ရန် လိုအပ်ပါသည်။

၎င်းကို ပြီးမြောက်စေရန် အသုံးအများဆုံးနည်းလမ်းတစ်ခုမှာ pairwise t-tests တစ်ခုစီအတွက် p-values များကို တွက်ချက်ရာတွင် Bonferroni တည့်မတ်မှုကို အသုံးပြုခြင်းဖြစ်သည်။

ဤသင်ခန်းစာတွင် Bonferroni တည့်မတ်ပုံကို R ဖြင့် ရှင်းပြထားသည်။

ဥပမာ- R တွင် Bonferroni အမှားပြင်ဆင်ချက်

မတူညီသော လေ့လာမှုနည်းပညာသုံးမျိုးသည် ကျောင်းသားအချင်းချင်း စာမေးပွဲရမှတ်များ ကွဲပြားစေခြင်း ရှိ၊ မရှိကို ဆရာတစ်ဦးမှ သိချင်သည်ဆိုပါစို့။

၎င်းကို စမ်းသပ်ရန်အတွက် လေ့လာမှုတစ်ခုစီကို အသုံးပြုရန် ကျောင်းသား ၁၀ ဦးကို ကျပန်းသတ်မှတ်ပေးသည်။ ၎င်းတို့၏ သတ်မှတ်ထားသော လေ့လာမှုနည်းစနစ်ကို အသုံးပြုပြီး တစ်ပတ်အကြာတွင် ကျောင်းသားတစ်ဦးစီသည် တူညီသောစာမေးပွဲကို ဖြေဆိုကြသည်။

တစ်လမ်းသွား ANOVA နှင့်ကိုက်ညီရန် R တွင်အောက်ပါအဆင့်များကိုသုံးနိုင်ပြီး အဖွဲ့တစ်ခုစီ၏စာမေးပွဲရလဒ်များကြားတွင်အတွဲလိုက်ခြားနားချက်များကိုတွက်ချက်ရန် Bonferroni အမှားပြင်ဆင်ချက်ကိုအသုံးပြုနိုင်သည်။

အဆင့် 1: ဒေတာအတွဲကို ဖန်တီးပါ။

အောက်ပါကုဒ်သည် ကျောင်းသား 30 ဦးလုံး၏ စာမေးပွဲရလဒ်များပါရှိသော ဒေတာအတွဲတစ်ခုကို ဖန်တီးနည်းကို ပြသသည်-

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

အဆင့် 2- အုပ်စုတစ်ခုစီအတွက် စာမေးပွဲရလဒ်များကို ကြည့်ပါ။

အုပ်စုတစ်ခုစီအတွက် စာမေးပွဲရလဒ်များ ဖြန့်ဝေမှုကို မြင်သာစေရန် boxplots များကို မည်သို့ထုတ်လုပ်ရမည်ကို အောက်ပါကုဒ်တွင် ပြသသည်-

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

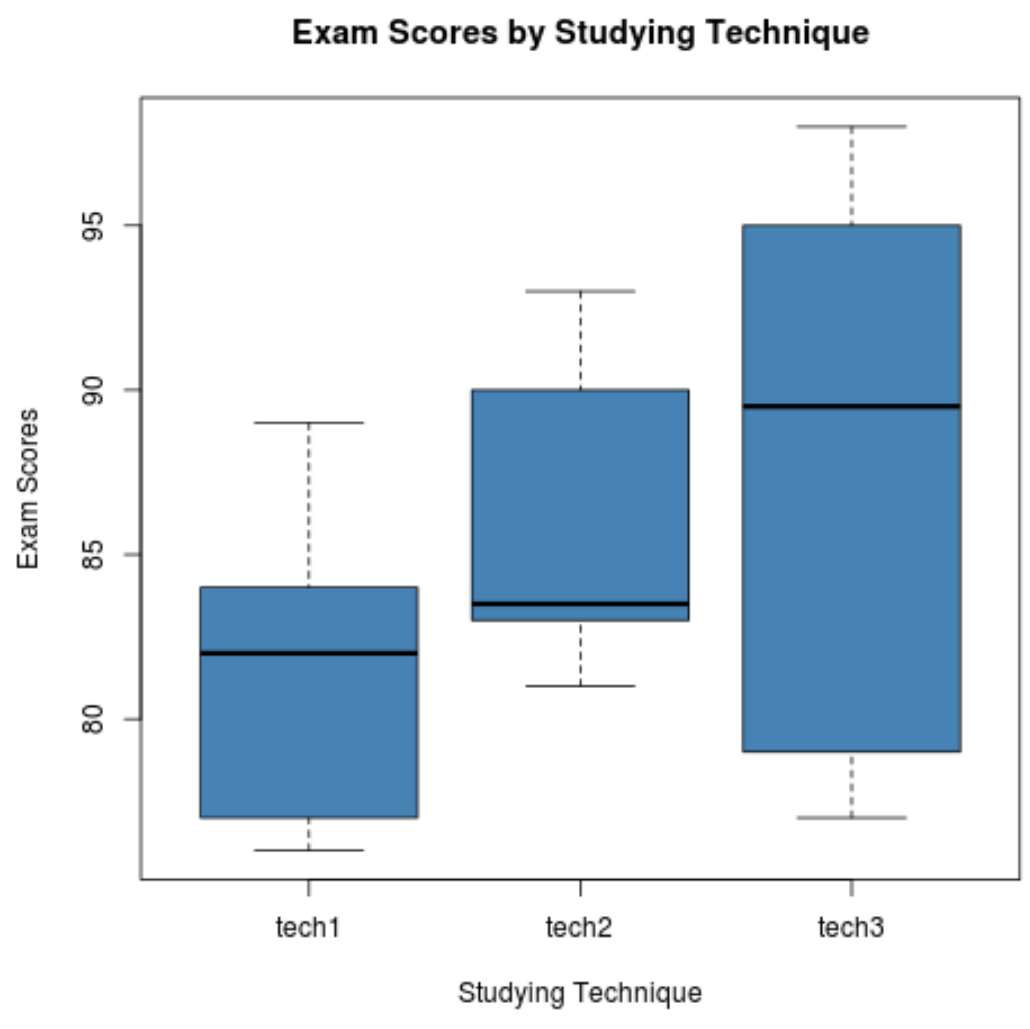
အဆင့် 3- တစ်လမ်းမောင်း ANOVA လုပ်ဆောင်ပါ။

အုပ်စုတစ်ခုစီရှိ ပျမ်းမျှစာမေးပွဲရမှတ်များကြား မတူညီမှုများကို စမ်းသပ်ရန်အတွက် အောက်ပါကုဒ်သည် တစ်လမ်းသွား ANOVA ကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

အလုံးစုံ p-တန်ဖိုး ( 0.0476 ) သည် 0.05 ထက်နည်းသောကြောင့်၊ အုပ်စုတစ်ခုစီတွင် တူညီသောပျမ်းမျှစာမေးပွဲရမှတ်မရှိခြင်းကို ညွှန်ပြသည်။

ထို့နောက်၊ အုပ်စုတစ်ခုစီ၏စာမေးပွဲရလဒ်များကြားတွင် pairwise ခြားနားချက်များကိုတွက်ချက်ရန် Bonferroni အမှားပြင်ဆင်ချက်ကို အသုံးပြု၍ t-tests များကိုလုပ်ဆောင်ပါမည်။

အဆင့် 4- pairwise t-tests ကိုလုပ်ဆောင်ပါ။

R တွင် Bonferroni တည့်မတ်မှုဖြင့် pairwise t-tests များကိုလုပ်ဆောင်ရန်၊ အောက်ပါ syntax ကိုအသုံးပြုသည့် pairwise.t.test() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်ပါသည်။

pairwise.t.test(x၊ g၊ p.adjust.method=”bonferroni”)

ရွှေ-

• x- တုံ့ပြန်မှုတန်ဖိုးများ၏ ကိန်းဂဏန်း vector တစ်ခု
• g- အုပ်စုများ၏အမည်များကိုသတ်မှတ်ပေးသော vector တစ်ခု (ဥပမာ-လေ့လာမှုနည်းပညာ)

အောက်ပါကုဒ်သည် ကျွန်ုပ်တို့၏ ဥပမာအတွက် ဤလုပ်ဆောင်ချက်ကို အသုံးပြုနည်းကို ပြသသည်-

 #perform pairwise t-tests with Bonferroni's correction
pairwise.t.test(data$score, data$technique, p.adjust.method=" bonferroni ")

	Pairwise comparisons using t tests with pooled SD 

data: data$score and data$technique 

      tech1 tech2
tech2 0.309 -    
tech3 0.048 1.000

P value adjustment method: bonferroni

ရလဒ်ကို အဓိပ္ပာယ်ဖွင့်ဆိုရန် နည်းလမ်းမှာ အောက်ပါအတိုင်းဖြစ်သည်။

• Technique 1 နှင့် Technique 2 အကြား စာမေးပွဲရမှတ်များ၏ ပျမ်းမျှကွာခြားချက်အတွက် ပြင်ဆင်ထားသော p-တန်ဖိုးသည် 0.309 ဖြစ်သည်။
• Technique 1 နှင့် Technique 3 အကြား စာမေးပွဲရမှတ်များ၏ ပျမ်းမျှကွာခြားချက်အတွက် ပြင်ဆင်ထားသော p-တန်ဖိုးသည် 0.048 ဖြစ်သည်။
• Technique 2 နှင့် Technique 3 အကြား စာမေးပွဲရမှတ်များ၏ ပျမ်းမျှကွာခြားချက်အတွက် ချိန်ညှိထားသော p-တန်ဖိုးသည် 1000 ဖြစ်သည်။

ရလဒ်များကို အခြေခံ၍ တစ်ခုတည်းသော သိသာထင်ရှားသော ခြားနားချက်မှာ နည်းစနစ် 1 နှင့် နည်းစနစ် 3 အကြားတွင်သာဖြစ်ကြောင်း ကျွန်ုပ်တို့ သိမြင်နိုင်ပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

One-Way ANOVA မိတ်ဆက်
R ဖြင့် တစ်လမ်းမောင်း ANOVA ကို မည်သို့လုပ်ဆောင်ရမည်နည်း
R တွင် Tukey စမ်းသပ်မှုပြုလုပ်နည်း
R တွင် Dunnett ၏စမ်းသပ်မှုကိုမည်သို့လုပ်ဆောင်ရမည်နည်း။